Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский федеральный университет им. И.Канта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matan_3_sem

.pdf

Скачиваний:

317

Добавлен:

10.02.2015

Размер:

17.04 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

436

Следствие. Если функция f (x,y)	непрерывна в прямоугольнике , то одно-
временно непрерывны функции I(x) на отрезке [c;d]			и J x непрерывна на отрезке
a;b . Тогда одновременно существуют интегралы
d	d b
			,
I y dy f x, y dx		dy	,
c	c a
b	b d
J x dx
J x dx	f x, y dy dx
a	a c
Эти интегралы называются повторными.
§ 4 Дифференцирование интегралов по параметру
Теорема. Пусть функция f (x,y)	непрерывна в прямоугольнике и имеет в
			b

нем непрерывную частную производную					fy x,y . Пусть I y f x, y dx,		y c;d .
Тогда:						a
Тогда:
1.	функция I(y) имеет на отрезке [c;d]
1.	функция I(y) имеет на отрезке [c;d]					производную I (y);
			b
	b		b			b
2.
2.	I y	fy x,y dx,	т.е. f x, y dx			fy x, y dx, y c,d ;
	a		a			a
3.
3.	I (y) непрерывна на отрезке [c,d].
Доказательство. Зафиксируем произвольную точку y0 c;d . Дадим прира-
щение	y 0 таким образом, чтобы y0			y c;d . Вычислим значение функции

I(y0) и I(y0 y):

I y0 f x,y0 dx,

a b

I y0 y f x,y0 y dx.

Найдем отношение приращения функции к приращению аргумента:

	I y y I y	0		b	f x,y	0	y f x,y	0
	0	0				0		0	dx
	y						y		dx
	y			a			y
Согласно теореме Лагранжа				a
Согласно теореме Лагранжа
f x, y0 y f x,y0 fy x, y0 y y,
где 0 1. Тогда
	I y y I y	0		b
	0	0	fy x,y0 y dx .
	y		fy x,y0 y dx .
	y			a
				a

(1)

(2)

По условию теоремы частная производная fy x, y непрерывна. Перейдем в соотношении (2) к пределу при y 0. Учитывая теорему о предельном переходе под знаком интеграла, получаем

lim	I y0 y I y0	b	lim	f x,y	0	y dx b	f x, y	0	dx.

y 0	y		y 0	y			y
		a				a

			437
			b
Следовательно, I y0 существует и I y0 fy x, y0 dx. В силу произвольности
			a
y0 c;d , делаем вывод о том, что		y	существует на всем отрезке c;d , кроме то-
y0 c;d , делаем вывод о том, что	I	y	существует на всем отрезке c;d , кроме то-
го,
		b
I y fy x,y dx.				(3)
		a

По условию теоремы fy x, y непрерывна, тогда из соотношения (3) и теоремы о

непрерывности интеграла как функции параметра следует непрерывность I (y)				на

отрезке [c,d].
	§ 5 Интегрирование интегралов по параметру
Теорема. Пусть функция		f (x, y)	непрерывна в прямоугольнике и
b	y c;d . Тогда
I y f x, y dx,	y c;d . Тогда
a
	d	b d
				(1)
	I y dy f (x, y)dy dx			(1)
	c	a c

Доказательство: Докажем более общее равенство:

t	b t		t c,d
				(2)
I y dy f (x,y)dy		dx,		(2)
c	a c

Рассмотрим левую часть равенства (2). В силу непрерывности функции

f (x, y) функция I(y) также непрерывна на отрезке c;d . Таким образом, в левой части равенства (2) мы имеем интеграл от непрерывной функции с переменным верхним пределом. Применим к нему теорему Барроу

t		b	t c,d .
		I(t) f (x,t)dx,		(3)
I(y)dy		I(t) f (x,t)dx,		(3)
c	t	a

Рассмотрим теперь правую часть равенства (2). Введем обозначение

t
f (x,y)dy x,t	(4)

Данная функция определена в прямоугольнике a x b,c t d . Докажем что она и непрерывна в этом прямоугольнике. Выберем произвольную точку x,t дадим приращение обеим переменным, так чтобы точка x x,t t . Получаем

			t t		t
		x x,t t x,t f x x,y dy f x,y dy
			c		c
	t		t t
	f x x, y f x, y dy f x x,y dy				(5)
	c		t
			. Если 0, то x 0
Пусть	x 2	t 2	. Если 0, то x 0	и t 0 одновременно. Возьмем

произвольное 0 и воспользуемся непрерывностью функции f (x, y) в прямоугольнике , тогда для выбранного 0 найдется 0, такое что, как толькобудет выполняться неравенство:

438

f x x,y f x, y

d c

Тогда если будет выполняться неравенство:

f x x,y f x, y dy

t c .

d c

Это означает, что

f x x,y f x,y dy 0

lim

Функция f (x, y) непрерывна в прямоугольнике (замкнутом множестве), то она на нем ограничена, следовательно, существует такое положительное число М, что f x, y M в прямоугольнике . Тогда

			t t
			f x x,y dy	M	t	.
				M	t	.

			t
	t t	f x x, y dy 0. Тогда из соотношения (5), получаем, что
Это означает, что		f x x, y dy 0. Тогда из соотношения (5), получаем, что
			0
	t		t 0
		x x,t t x,t 0,
				0

что означает непрерывность функции x,t в произвольной точке x,t , следовательно, функция x,t непрерывна в прямоугольнике . Из соотношения (4) по теореме Барроу следует

	x,t		t
						f (x,t) .	(6)
t			f (x,y)dy			f (x,t) .	(6)
			c		t
По условию теоремы функция		f (x, y)		непрерывна в прямоугольнике , следова-

тельно, и t x,t непрерывна в этом прямоугольнике. С учетом равенства (4), запи-

шем правую часть равенства (2) в виде

b t	f x,y dy		b
				(7)
		dx (x,t)dx.
a c			a
В правой части равенства (7) переменная t			выступает в качестве параметра. Ранее
мы показали, что функция x,t непрерывна в прямоугольнике и имеет в нем

непрерывную частную производную t x,t . По теореме о дифференцировании по параметру под знаком интеграла получаем

		b
(x,t)dx		t
(x,t)dx		t
	t	a

b	t c,d .
(x,t)dx f (x,t)dx,	t c,d .	(8)

Из анализа соотношений (3) и (8) приходим к выводу о том, что левая и правая части равенства (2) имеют на отрезке c;d совпадающие производные, следовательно, они отличаются на константу.

t b		b t

f x, y dx	dy
c a		a c

f x,y dy dx const. (9)

В последнем равенстве положим t c, получим 0 0 const , тогда const 0 и получаем равенство

439

t b		b t
				(10)
f x, y dx	dy f x, y dy		dx.	(10)
c a		a c

Наконец, положив t d , получаем требуемое равенство

d b		b d

f x, y dx	dy f x, y dy		dx
c a		a c

Теорема доказана.

§ 6 Пределы интегрирования, зависящие от параметра

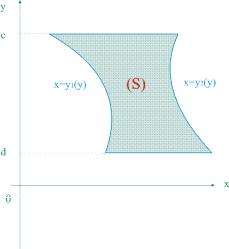
Пусть функция f (x, y) определена в плоской области (S), ограниченной ли-

ниями y=c, y=d (c<d) и x y1 y ,	x y2 y , где y1 y ,	y2 y - функции, непрерывные
на отрезке c,d .

При каждом фиксированном y c,d существует	y2 y
При каждом фиксированном y c,d существует	f x, y dx. Каждому значению
	y1 y

y будет соответствовать определенное значение интеграла. Следовательно,

y2 y

f x, y dx является функцией переменной (параметра) y , определенной на отрез-

y1 y

ке c,d . Введем обозначения:

		y2 y		y c,d
		I(y) f x,y dx,		y c,d		(1)
		y1 y
	Примем без доказательства два утверждения.
	Теорема 1. Пусть функция f (x, y) непрерывна в плоской области (S) и
	y2 y	y c,d . Тогда функция I(y) непрерывна на отрезке c,d .
I(y)	f x,y dx,	y c,d . Тогда функция I(y) непрерывна на отрезке c,d .
	y1 y
	Теорема 2. Пусть функция f (x, y) непрерывна в плоской области (S) и имеет
на ней непрерывную частную производную			f	y	(x,y). Пусть функции y y ,	y y
				y	1	2

определены на отрезке c,d и имеют на нем непрерывные производные

							440
y1 y ,	y2 y . Пусть I(y)			y2 y			y c,d . Тогда для любого y c,d суще-
y1 y ,	y2 y . Пусть I(y)			f x,y dx,			y c,d . Тогда для любого y c,d суще-
ствует		y , причем		y1 y

	I
			y2 y							y

		I (y)		fy	x,y dx f y2(y),y y2				y - f y1(y),y y1
			y1 y
Пример Дан интеграл I y						1		dx. Найти lim I y .
Пример Дан интеграл I y							x2 y2	dx. Найти lim I y .
									y 0
						1

Подынтегральная функция f (x,y) x2 y2 непрерывна на всей плоскости Оху, следовательно, будет непрерывна в любом прямоугольнике

1 x 1, d y d , где d 0 . По теореме из §2 возможен предельный переход по параметру под знаком интеграла

	1									1
lim			x2		y2 dx							lim			x2 y2 dx
y 0											y 0
	1										1
		1						0						1
					x	dx xdx xdx


			1					1						0
				x2			0		x2		1		1			1	1.
				x2					x2				1			1

					2		1	2			0	2		2
					2		1	2			0

441

Глава 18

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА

§1 Определение равномерной сходимости
Пусть функция f x, y задана в области a x ,		Пусть при каждом фик-
c y d.

сированном y c;d несобственный интеграл f x, y dx	сходится. Тогда f x, y dx
a		a

будет представлять собой функцию переменной (параметра) у, определенную на

отрезке c;d . Будем обозначать ее I y , где					y c;d .

Наше утверждение, что несобственный интеграл f x, y dx сходится при
каждом y c;d . Это означает,							a
каждом y c;d . Это означает,	что при каждом фиксированном y c;d
		A	f x, y dx
lim			f x, y dx			f x, y dx.
A
		a			a
Тогда
			x, y dx	A	f		0
lim		f	x, y dx		f	x, y dx	0
A
a				a

Используя свойства аддитивности определенного интеграла, запишем эквивалентную формулу

lim f x, y dx 0

По определению это означает, что для каждого y c;d для любого > 0 найдется число М > 0 , такое, что из неравенства А>M будет следовать неравенство

f x, y dx

Заметим, что число М выбирается по > 0 для каждого y c;d , т.е. выбор его зависит и от и от у.

Если для > 0 можно указать число М > 0, зависящее только от (т.е. для всех y c;d одно и то же) такое, что из неравенства А>M будет следовать неравенство

f x, y dx

Сразу для всех y c;d , то говорят, что несобственный интеграл f x, y dx сходит-

ся по параметру равномерно.

442

Аналогичным образом вводится понятие равномерно сходящегося по параметру несобственного интеграла второго рода.

Пусть функция	f x,y задана в прямоугольнике	a x b;c y d
(здесь a,b,c,d - конечные числа).
Пусть при каждом фиксированном y c;d несобственный интеграл
b	b

f x, y dx сходится. Тогда f x, y dx будет представлять функцию переменной

a	a
(параметра)	y c;d .

Последнее утверждение означает, что при каждом фиксированном y c;d

				f x, y dx	b	f x, y dx
lim				f x, y dx		f x, y dx
b 0
			a		a
		b		f x, y dx		f x, y		0
lim				f x, y dx		f x, y	dx	0
b 0
		a			a
	b					b	f x, y dx 0.
lim		f x, y dx 0 lim					f x, y dx 0.
b 0						0

(Мы ввели обозначения: b b ).

Последнее равенство по определению предела означает, что для каждого y c;d для любого > 0 найдется такое число >0 , такое, что из неравенства 0 следует неравенство

f x, y dx

Следует отметить, как и в случае несобственного интеграла первого рода, число >0, выбираемое по будет, вообще говоря, для каждого y c;d свое.

Если же для любого > 0 можно найти число >0 зависящее только от (т.е. одно и то же для всех y c;d ), такое что из неравенства 0 следует неравенство

f x, y dx ,

То несобственный интеграл f x, y dx называется равномерно сходящимся по па-

раметру у на отрезке c;d .

§2 Непрерывность интеграла как функции параметра

	Теорема. Пусть	a x b;c y d ;
1.	функция f x,y непрерывна в прямоугольнике	a x b;c y d ;

2.	несобственный интеграл f x, y dx сходится равномерно относительно у на

отрезке c;d .

Тогда функция I y непрерывна на отрезке c;d .

443

Доказательство. Зафиксируем произвольное y0 c;d . Выберем произволь-

ное > 0.

По условию теоремы интеграл f x, y dx сходится равномерно по перемен-

ной у на отрезке c;d , поэтому по выбранному > 0 найдем число М>0, зависящее только от , такое, что для всякого числа А>M, сразу для всех y c;d будет выполняться неравенство

	f x, y dx
			.	(1)

A		3

Выберем и зафиксируем число А, удовлетворяющее условию А>M. Введем

обозначение A y f x, y dx. В выбранных обозначениях неравенство (1), спра-

ведливое для всех y c;d , запишется в виде
	I y y				(2)


		A		3
				3
Рассмотрим подробно разность, стоящую под знаком модуля в неравенстве (2)
			A
I y A y f x, y dx f x, y dx f x, y dx
	a		a		A

A y - это собственный интеграл, зависящий от параметра. Из теоремы о непрерывности собственных интегралов, зависящих от параметра, следует, что A y непрерывна на отрезке c;d , а значит по теореме Кантора и равномерно непрерывна на нем.

Тогда для любого > 0 найдется >0, зависящее только от , такое, что для двух произвольных точек y и y из c;d , для которых выполнено y y , то-

гда будет выполняться неравенство

A y A y .

Имеем

I y I y I y A y A y A y A y I y ,

тогда

I y I y I y A y A y A y

A y I y

Если выбрать y y0 , y y , где y c;d произвольное число, но такое, что

y y0

, тогда будет выполняться неравенство

I y I y0

. Это означает, что

функция I y непрерывна в точке y0 . Так как мы выбирали произвольную точку y0 c;d , то приходим к выводу о непрерывности функции I y на отрезке c;d . Теорема доказана.

§3 Интегрирование по параметру под знаком интеграла

a x ,

Теорема. Пусть функция f x,y непрерывна в области

c y d.

444

	сходится равномерно относительно у на c;d .
1. f x,y dx	сходится равномерно относительно у на c;d .
a
Тогда справедливо равенство:
	d	f x, y dx		d
						(1)
			dy	f x,y dy	dx ,	(1)
	c a			a c

причем несобственный интеграл, стоящий в правой части равенства (1) сходится. Доказательство. Возьмем произвольное > 0. По условию теоремы

f x,y dx сходится равномерно относительно у на c;d , поэтому для выбранного

> 0 найдется число М>0, зависящее только от , такое, что как только возьмем число А>M, то сразу для всех y c;d будет выполняться неравенство


f (x,y)dx		.

A	d c

Зафиксируем некоторое число А, удовлетворяющее неравенству А>M. Вводя

как и раньше обозначения A y f x, y dx, сразу для всех y c;d неравенство

можно записать в виде

I y y

d c

Так как функции

I y и A y

непрерывны на отрезке c;d , то они и интегри-

руемы на нем. В силу свойств интегралов

I y dy A y dy I y A y dy

тогда

d c

I(y)dy A(y)dy

I(y) A

(y)

d c

Мы получили, для любого > 0 существует число М, что при любом А>M, выполняется неравенство

			d	d
			I(y)dy A(y)dy			.
			c	c
Это означает что
	d	y dy		d	I y dy ,
lim		y dy			I y dy ,		(2)
A			A
	c			c

но A y f x, y dx - собственный интеграл, зависящий от параметра у. По теоре-

ме об интегрировании по параметру собственного интеграла можем записать

d	d A	f x.y

A y dy
c	c a

dx		A d

	dy f x,y dy		dx.
		a c

Тогда равенство (2) можно записать в виде

445

d	I y dy lim	A d
	I y dy lim		f x,y dy dx
	A
c		a c

Ранее мы доказали существование предела, следовательно можно его записать иначе

	d
	f x, y dy

		dx
a c

Следовательно доказана сходимость интеграла, из правой части равенства (1) и справедливость самого равенства.

Теорема доказана.

§ 4 Дифференцирование по параметру под знаком интеграла

Теорема.

1.	Пусть функция		a x ,	и имеет в ней не-
1.	Пусть функция		f x,y непрерывна в области	и имеет в ней не-
			c y d
	прерывную частную производную fy x,y ;
		сходится при каждом y c;d ;
2.	I y f x, y dx	сходится при каждом y c;d ;
	a
			сходится равномерно относительно у на c;d ;
3.	y fy x,y dx		сходится равномерно относительно у на c;d ;

Тогда:

1.
1.	I y существует при каждом y c;d ;

						x, y dx;
2.
2.	I	y y , т.е.	f x,y dx	y	f
			a		a
3.		y непрерывна на c;d .
3.	I	y непрерывна на c;d .

Доказательство:

a x ,

Так как fy x, y непрерывна в области иc y d

fy x,y dx сходится рав-

номерно относительно у на c;d то по теореме из §2 и y dy существует. В ча-

стности существует интеграл y dy для любого z , удовлетворяющего условию

c z d. По теореме из §3 имеем

z		z			z		x, y dy

y dy			fy x, y dx dy			fy		dx.
c		c a			a c
z
Но fy x,y dy f x,y	yy cz	f x,z f x,c . Поэтому
Но fy x,y dy f x,y	yy cz	f x,z f x,c . Поэтому
c
z
y dy f x,z dx f x,c dx I z I c ,
c
c		a		a
			I z		I c

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.10.2018123.39 Кб317magister-economic-psychology.doc
#
10.02.201579.36 Кб370MakKueyl_D.doc
#
23.03.2016441.86 Кб445Maksakov.doc
#
23.03.20165.38 Mб12210Manipulyatsii_v_SD_Broshyura.doc
#
10.02.20155.14 Mб516matan_3_sem.doc
#
10.02.201517.04 Mб317matan_3_sem.pdf
#
10.02.20151.03 Mб320Maykl_Kan_Mezhdu_Psikhoterapevtom_I_Klientom.doc
#
23.03.2016928.26 Кб331meh_lab БФУ.doc
#
16.08.20191.01 Mб269meh_lab.doc
#
10.02.2015321.54 Кб112Meine Sommerferien.doc
#
17.04.2019252.74 Кб28menedzhment_otvety.docx