matan_3_sem

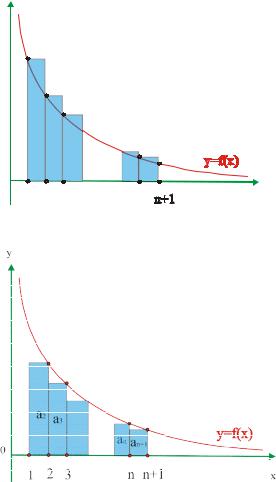
386

1) Если несобственный интеграл f x dx сходится, то сходится и ряд (1);

1

2) Если указанный интеграл расходится, то расходится и ряд (1).

Для доказательства рассмотрим геометрическую интерпретацию интеграла и частичных сумм ряда (1).

y

a1

a2

a3

Рис. 1

Рис. 2

Рисунок 1 поясняет тот факт, что площадь ступенчатой фигуры равна (т.к. площадь одного прямоугольника равна произведению соответствующего члена ряда- высоты на единицу – длину основания)

a1 a2 ... an Sn .

С другой стороны, площадь криволинейной трапеции, ограниченной графиком функции, прямыми x 1, y n 1 и осью ОХ можно вычислить с помощью опреде-

n 1

ленного интеграла f (x)dx. Имеем неравенство

В результате приходим к неравенству

388

§4 Признаки сходимости рядов с положительными членами

Теорема 1 (признак Даламбера). Дан ряд с положительными членами

Доказательство. Воспользуемся определением предела последовательности. Рассмотрим случай, когда l 1, выберем произвольное число 0 так, чтобы чис-

ло q l 1.

Из определения предела последовательности следует, что начиная с некоторого номера n0 , для всех n n0 выполняется неравенство

да (1), а следовательно, сходится ряд (1).

389

2). Рассмотрим случай, когда l 1,

Тогда из неравенства (3) следует, что n n0

an 1 q an 1 q an an

Следовательно, начиная с номера n0 не выполняется необходимое условие сходимости ряда, значит в этом случае ряд (1) расходится.

2n 1

Пример. Исследовать сходимость ряда n 1 n! .

Воспользуемся признаком Даламбера. Найдем an 1

Из полученного результата делаем вывод, что исследуемый ряд сходится.

Терема 2 (признак Коши). Пусть для ряда (1) с положительными членами существует предел

Тогда

1)если k 1, то ряд (1) сходится;

2)Если k 1, то ряд расходится.

Воспользуемся определением предела последовательности.

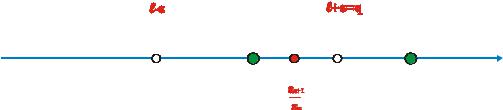
Рассмотрим случай, когда k 1. Выберем произвольное, достаточно малое число0, так чтобы q k 1 (рис. 3)

Рис. 3

Тогда из равенства (4) следует, что существует такой номер n0 , что для всех n n0 Будет выполняться неравенство

Из неравенства (5) следует, что для n n0

nan k q an qn .

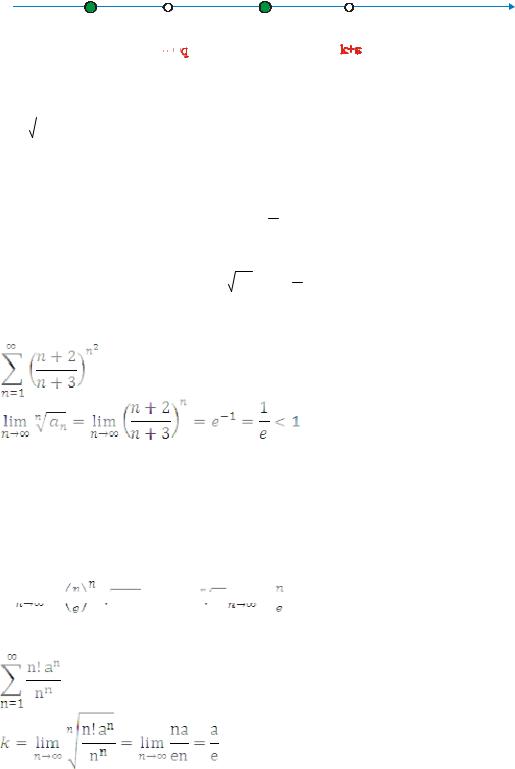
390

Из сходимости ряда qn и признака сравнения ряд (1) в этом случае сходится.

n 1

2) Пусть k 1.

1 k

Тогда, обозначив k q 1, из определения предела получаем, что для n n0

нения следует расходимость ряда (1).

Примеры.

3 n

1.Исследовать на сходимость ряд .

nn 1

Применим признак Коши. Найдем

k lim n an lim 3 0 1.

n

Исследуемый ряд сходится.

2.Исследовать на сходимость ряд

Следовательно, исследуемый ряд сходится.

Замечание 1

Если в признаке Коши k 1 или в признаке Даламбера l 1то эти признаки не дают ответа на вопрос о сходимости исследуемого ряда.

Замечание 2

При использовании радикального признака Коши удобно использовать формулу Стирлинга и следствие из неё ([Ф] т2. стр. 369-371.))

, тогда

3. Пример: Исследовать на сходимость ряд, при

Следовательно, при , ряд сходится, а при - расходится Приведем без доказательства несколько признаков сходимости рядов с по-

ложительными членами ([2] стр. 266-271, [Ф] т2. стр. 305-320.)

Признак Раабе

Пусть дан ряд (1) с положительными членами. Пусть

и существует конечный или бесконечный предел R lim Rn . Тогда:

n

1)если R 1 то ряд (1) сходится;

2)если R 1 то ряд (1) расходится.

Признак Бертрана

Пусть дан ряд (1) с положительными членами. Пусть

и существует конечный или бесконечный предел B lim Bn . Тогда:

n

1)если B 1 то ряд (1) сходится;

2)если B 1 то ряд (1) расходится.

Замечание

Если в признаке Раабе R 1 или в признаке Бертрана B 1то эти признаки не дают ответа на вопрос о сходимости исследуемого ряда.

Признак Гаусса.

Пусть дан ряд (1) с положительными членами. Пусть отношение an можно

1)1 ( - любое), то ряд (1) сходится;

2)1 ( - любое), то ряд (1) расходится;

3)1, 1, то ряд (1) сходится;

4)1, 1, то ряд (1) расходится.

§5 Знакочередующиеся ряды

Определение. Числовой ряд, у которого два соседних члена имеют противоположные знаки, называется знакочередующимся рядом.

Такой ряд можно представить в виде

n 1

Для знакочередующихся рядов имеется достаточный признак, часто используемый на практике

Теорема. (Признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине и предел общего члена равен нулю, то ряд (1) сходится.

Доказательство. Из условия теоремы следует

394

Доказательство. Пусть ряд (1) сходится абсолютно. Это будет означать, что для него выполнен критерий Коши сходимости ряда, т.е. для 0 существует номер n0 , такой, что для всех n n0 выполнялось неравенство

an 1 an 2 an 3 ... an p

для всех натуральных p . Используем свойства абсолютной величины числа, получаем

Приходим к выводу, что для знакопеременного ряда (1) выполнен критерий Коши, следовательно, он сходится.

Определение. Если ряд (1) сходится, но не абсолютно, он называется услов-

но сходящимся рядом.

Перестановка членов в сходящихся рядах.

Теорема (о перестановке членов ряда). Если ряд

n1

сположительными членами сходится, то после произвольной перестановки членов

ряда, полученный ряд будет также сходиться, причем к той же сумме.

Доказательство. Пусть S – это сумма сходящегося ряда (1), т.е. S lim Sn , где

n

Sn частичные суммы ряда (1). Переставим произвольным образом члены ряда (1), получим ряд

Обозначим S~i i ю частичную сумму ряда (4).

Вычислим наибольший номер из i членов ряда (4), входящих в частичную сумму

(5). k max n1,n2,n3,...,ni . И рассмотрим Sk - частичную сумму ряда (3) с номером k . Очевидно, что все члены ряда из частичной суммы (5) будут содержаться в Sk .

Тогда S~i Sk . В силу того, что члены ряда (3) положительны, то любая его частич-

ная сумма, в том числе и Sk , не превосходит суммы ряда, таким образом, приходим к неравенству

Мы получили, что неубывающая последовательность S~i ограничена сверху - значит, она имеет предел. Пусть

S~ lim S~n .

n

Из неравенства (6) после предельного перехода будет следовать, что S~ S . Полу-

чается, что при перестановке членов ряда сумма не увеличивается, но она не может и уменьшиться, т.к. при обратной перестановке сумма бы увеличивалась, что про-

тиворечит полученному результату. Тогда

S~ S .

Теорема доказана.