matan_3_sem

396

Ранее было доказано, что ряд, полученный из сходящегося ряда с положительными членами, путем перестановки членов этого ряда, также сходится. Ряд

называется произведением рядов (1) и (2).

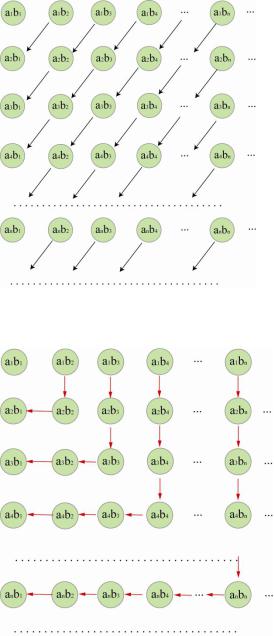
Заметим, что произведение по аналогии с конечными произведениями можно располагать различными способами. На рисунке 7.1 произведение и группировка слагаемых осуществляется «по диагонали». На рисунке 7.2 «по квадратам».

Первый способ приводит к сумме

397

Рис. 7.1

Рис. 7.2

Теорема (Коши) Если ряды (1) и (2) сходятся абсолютно и имеют суммы А и В, то произведение этих рядов сходится абсолютно и имеет сумму АВ.

Доказательство. Рассмотрим ряды, составленные из абсолютных величин членов рядов (1) и (2)

Следуя [2], обозначим суммы рядов (6) и (7) A* и B* (по условию теоремы ряды

(6) и (7) сходятся).

Расположим члены ряда-произведения произвольным образом

398

p 1

иего частичную сумму, при этом введем обозначение

max i1,i2,i3,...,ip ,k1,k2,k3,...,kp

a1 a2 a3 ... a b1 b2 b3 ... b A* B*

Следовательно, ряд (3) сходится абсолютно.

Для нахождения суммы этого ряда расположим его члены, как на рис. 7.2 («по квадратам»).

a1b1 a2b1 a2b2 a1b2 a1b3 a2b3 a3b3 a3b2 a3b1 ...

Обозначаем привычным образом частичные суммы рядов (1) и (2) An и Bn соответственно. Тогда последовательность частичных сумм ряда (5) можно записать в виде

A1B1, A2B2, A3B3,...,AnBn,...

Эта последовательность сходится к AB, следовательно, это и есть сумма ряда (3). Теорема доказана.

Замечание 1. Если ряды (1) и (2) сходятся не абсолютно, то ряд (3) может сходиться, а может и расходиться.

Замечание 2. Имеет место теорема Мартенса. Если ряды (1) и (2) сходятся, причем один из них абсолютно, то их произведение (3) сходится и справедливо соотношение

Где А, В, С – суммы рядов (1), (2), (3) соответственно.

Замечание 3. (Теорема Абеля)

Если каждый из рядов (1) и (2) сходится условно, а также ряд (3) сходится, то для сумм этих рядов справедливо равенство (10).

Глава 15. Функциональные ряды.

§1. Функциональные ряды. Основные понятия.

Пусть Un (x) n 1 U1(x);U2 (x);U3 (x)...-последовательность функций, заданных на некотором множестве Х.

в котором члены последовательности Un (x) соединены знаками плюс, называют

функциональным рядом, определенным на множестве Х.

Функции U1(x);U2 (x)...Un (x)...- члены этого функционального ряда.

399

При фиксированном x0 X всякому функциональному ряду Un (x) соответству-

n 1

ет числовой ряд Un (x0 ), членами которого являются значения Un (x0 )функций

n 1

Un (x) в точке x0 .

Определение. Функциональный ряд (1.1) называют сходящимся в точке x0 X ,

если сходится числовой ряд Un (x0 ).

n 1

Точка x0 называется точкой сходимости функционального ряда (1.1) . Множество всех точек сходимости функционального ряда называется его областью сходимости.

Такую сходимость функционального ряда называют поточечной.

n

Определение. Конечная сумма Sn (x) U1(x) U2 (x) ... Un (x) ... Uk (x) называ-

k 1

ется n-ной частичной суммой ряда(1.1).

Определение. Функция S(x) limSn (x) , определенная в области D называется сум-

x

мой ряда (1.1).

Определение. Для всякого n N функциональный ряд Uk (x), x X называют n-

k n 1

ным остатком функционального ряда (1.1).

Можно записать критерий Коши сходимости функционального ряда.

Функциональный ряд (1.1) сходится на множестве Х тогда и только тогда, когда для x X и 0 n0 (x, ) N (зависящее от х и ), такое, что для всех n n0 (x, )и

n m

m N : Sn m (x) Sn (x) Uk (x) .

k n 1

Определение. Функциональный ряд (1.1) называется абсолютно сходящимся на

множестве D X , если в любой точке k этого множества сходится ряд Un (x).

n 1

Замечание. Для определения абсолютной сходимости функционального ряда используют признаки Коши и Даламбера.

Примеры.

Найти область сходимости:

1. lnn 1 x, Область определения: x 0.

n 1

(ln x)n 1 1 ln x ln2 x ...-это геометрическая прогрессия,у которой

n 1

400

cosnx

2. n 1 n n ; Область определения:x R.

x 0- ряд абсолютно сходится; x 0-расходится;

при x 0:

Ряд условно сходится по признаку Лейбница .

§2. Равномерная сходимость функциональных последовательностей и рядов.

Функциональные ряды обычно начинают изучать с исследования его на сходимость, которое сводится к определению области сходимости этого ряда.

При этом можно использовать известные свойства числовых рядов и их признаки сходимости.

Таким образом, выделяют области абсолютной и условной сходимости. Другая и более сложная задача теории функциональных рядов - нахождение их суммы.

Запишем определение поточечной сходимости последовательности на языке символов:

Un(x) U(x) 0, x X n0( ,x): n n0( ,x)

Определение. Функциональная последовательность Un (x) называется равномерно сходящейся к функции U(x) на множестве Х, если

Замечание:

(3).

Замечание:

401

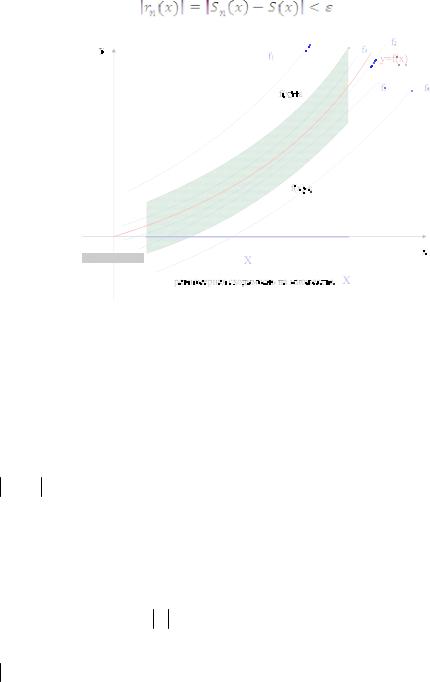
Отличие поточечной и равномерной сходимости состоит в том, что в первом случае номер n0 зависит от и x X , а во втором - только от .

Определение. Ряд Un (x), членами которого являются функции, определенные на

n 1

Х, называется равномерно сходящимся на этом множестве, если последовательность его частичных сумм равномерно сходится на Х, то есть 0 n0( ): n n0 и

x X :

(4)

Для функционального ряда справедлива:

Теорема (признак Вейерштрасса).

Если члены функционального ряда Un (x) удовлетворяют неравенствам:

n 1

Un (x) an, n N, x X (5) и числовой ряд an , an 0-сходится, то функцио-

n 1

нальный ряд сходится равномерно в области Х.

Доказательство:

Так как числовой ряд сходится, то его остаток стремится к нулю (rn 0), то есть

0 n0( ): n n0 : rn .

лению равномерной сходимости ряд Un (x)-равномерно сходится в области Х.

n 1

402

Числовой ряд an , члены которого удовлетворяют неравенству (2.5), называется

n 1

мажорантным рядом или мажорантой для функционального ряда (1.1).

Функциональный ряд называется мажорируемым на множестве Х.

Замечание:

Признак Вейерштрасса является достаточным для абсолютной сходимости ряд.

Теорема

Для последовательности функции и функции U(x), определённых на множестве , Справедливо следующее утверждение:

Справка:

Число называется верхней гранью множества Х, если:

1) уд. неравенству

2)Для

х

Поэтому для конечная точная верхняя грань:

Используя свойство точной верхней грани и определение (*) имеем:

б) Пусть

Согласно свойству точной верхней грани, для всех верно неравенство:

403

последовательность его частичных сумм равномерно сходится на .

Следствие.

Для равномерной сходимости функционального ряда Un x , необходимо и дос-

n 1

таточно, чтобы limsuprn x 0

n x X

Пример:

Выяснить, является ли функциональный ряд равномерно сходящимся:

По признаку Лейбница этот ряд сходится в

Оценим остаток ряда :

В силу свойства точной верхней грани.

т.е.

§3. Свойства равномерно сходящихся рядов

Замечание: Если два функциональных ряда Un x и Vn x сходятся на мно-

n 1 n 1

жестве X равномерно, то всякая их линейная комбинация , Un x Vn x где

n 1

, R так же является равномерно сходящимся рядом на множестве X.

405

при х=1 0+0+0+… ряд сходится; Частичные суммы ряда

1 x x x2 x2 x3 ... xn xn 1 1 xn 1.

Тогда предел частичных сумм

1, если0 x 1

S x

0, если x 1.

Остаток ряда rn x S x Sn x .

sup rn x 1 0

0 x 1

Следовательно, данный ряд сходится неравномерно на исследуемом отрезке. Примечание. Если функциональный ряд непрерывных на сегменте функций сходится на этом сегменте к разрывной функции, то ряд сходится неравномерно.

Замечание (следствие теоремы о непрерывности суммы неравномерно сходящегося ряда)

Если сумма S(x) функционального ряда с непрерывными членами разрывна в области X, то этот ряд в области X сходится неравномерно.

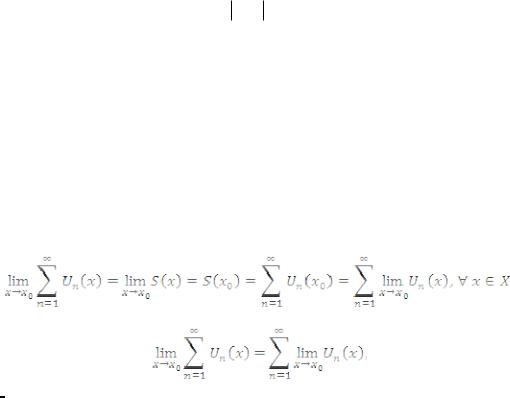
Следствие : В равномерно сходящемся ряде возможен почленный переход к

пределу. Un x – сходится равномерно тогда S(x) - непрерывная функция.

n 1

т.е.

Теорема (о почленном интегрировании функционального ряда).

Если функциональный ряд Un x с непрерывными членами сходится к

n 1

функции S(x) равномерно на [a,b], то его можно почленно интегрировать на любом отрезке x0,x a,b и справедливо равенство:

и ряд Un t сходится равномерно на отрезке [a;b].

n 1

Доказательство:

1.Согласно теореме о непрерывности равномерно сходящегося функцио-

нального ряда функция S t Un t непрерывна на отрезке [a;b], следовательно,

n 1

она интегрируема на любом отрезке x0,x a,b .

2. Ряд Un t сходится равномерно на отрезке [a;b] это означает, что

n 1