
Случайный процесс
.pdf
R |
|
|
|
1 |
|
|
|
Rη(t1 |
,t2) |
|
η |
|
|
(t |
|
,t |
|
) |
1 |
. |
|
|
R |
η |
2 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|||
Двумерная плотность распределения равна
1
wξ (y1,y2,t1,t2)  πN0
πN0 
 t1 t2
t1 t2  1 R2η(t1,t2)
1 R2η(t1,t2)
|
|
1 |
|
|
|
|
2 |
|
|
y1 y2 |
2 |
|
|
|
|
|
|
|
|
2y1 |
|
|
|
2y2 |
|
||
exp |
|
2 |
,t2) |
2 |
|
|
N0 t1 |
Rη(t1 |
,t2) |
N0 t1 t2 |
|
N0 t2 |
|
|
|
2(1 Rη(t1 |
|
) |
|
|
|
|
|||||
Винеровский процесс будет также марковским. Рассмотрим три момента времени ti 2 ti 1 ti и запишем трехмерную плотность вероятности
wη(yi 2,yi 1,yi,ti 2,ti 1,ti)
wη(yi 2,ti 2) wη(yi 1,ti 1 / yi 2,ti 2) wη(yi,tt / yi 1,yi 2,ti 1,ti 2)
Используя равенство (2.58), запишем
ti ti 1 ti ti
η(ti) ξ(τ)dτ |
ξ(τ)dτ |
ξ(τ)dτ η(ti 1) |
ξ(τ)dτ. |
0 |
0 |
ti 1 |
ti 1 |
Из последней формулы видно, значения процесса в момент ti не зависит от момента времени ti 2 и поэтому можно записать
wη(yi 2,yi 1,yi,ti 2,ti 1,ti)
wη(yi 2,ti 2) wη(yi 1,ti 1 / yi 2,ti 2) wη(yi,tt / yi 1,ti 1). (2.61)
Формулу (2.61) можно обобщить и получить формулу (2.41). 2.7.4. Марковские цепи
Положим, случайный процесс ξ(t) в дискретные моменты вре-
мени t0,t1,t2,t3, может принимать дискретные значения xj из |
не- |
которого конечного множества X с числом элементов, равным |
K. |
Припишем номер каждому состоянию xj j. Состояние xj в момент |
|
t0 будем считать начальным состоянием процесса, описываемое рас- |
|
пределением вероятностей P(ξ(t0) j), |
j 1,2, ,N. Условные ве- |
роятности (вероятности перехода) |
|
63
P(ξ(tm n ) k/ξ(tm) j) πjk (n) |
(2.62) |
показывают вероятность перехода из состояния xj j в момент вре-
мени tm в состояние xk k за n шагов (n 1,2, , j, k 1,2, , N). Если вероятности перехода (2.62) не зависит от момента времени tm , а зависит только от n,то такая марковская цепь называется однородной. Вероятности перехода однородной цепи Маркова образуют матрицу π(n):
|
|
π |
11 |
(n) |
π |
12 |
(n) |
|
|
|
π |
(n) |
π |
(n) |
|||
π(n) |
|
21 |
22 |
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
π |
(n) |
π |
||||
|
|
N1 |
N2 |
(n) |
||||
|
|
|
|
|
|
|||
π |
1N |
(n) |
|
|
|
|
|
π2N (n) |
|||
|
|
|
. |
|
|
||
πNN (n) |
|
||
|
|||
Вероятности перехода удовлетворяют условию нормировки
N
πjk (n) 1.
k 1
Для условных вероятностей (2.62) справедливо уравнение Марко-
ва
N |
|
|
πjk (n m) πj i (n) πik (m) , |
n 0,m 0, |
(2.63) |
i 1 |
|
|
или в матричной форме |
|
|
π(n m) π(n) π(m), |
(2.64) |
|
которое называется также уравнением Колмогорова-Чепмена. Уравнение Маркова позволяет вычислить условные вероятности
перехода πjk (n m) в состояния (j, k) 0 j, k N за n m испытаний.
Вероятность того, что случайный процесс будет находиться в состоянии k через m n испытаний равна
N |
|
|
πk (m n) πi (m) πik (n) , |
n 0,m 0 , |
(2.65) |
i 1
которое также называется уравнением Маркова [11]. В частности, если m 0, получим
64
P(ξ(tn ) k) πk (n)
N |
|
|
|
|
πi (0) πik (n) , |
k 1,2, ,N, |
n 0, |
(2.66) |
|
i 1 |
|
|
|
|
т.е. зная распределение |
вероятности |
πi(0) P(ξ(t0) i), |
||
i 1,2, ,N состояния случайного процесса в момент времени t0 и вероятности перехода πij(n), можно найти распределение вероятно-
сти состояния случайного процесса в момент времени tn. Рассмотрим более подробно (2.64). Положим m 1, n 1, 2, . То-
гда имеем
π(2) π(1) π(1) π2(1);
π(3) π(2) π(1) π3(1);
Продолжая эту процедуру, определим для произвольного n матрицу вероятности переходов за n испытаний как степень матрицы вероятности переходов за одно испытание
π(n) πn(1). |
(2.67) |
Перепишем формулу (2.66), используя (2.67) в матричной форме |
|
π(n) πT (0) πn (1), |
|
где πT (0) - транспонированный вектор распределения вероятно- |
|
сти состояния случайного процесса в момент времени t0. |
|
Если за конечное число n шагов процесс из состояния xi |
может |
попасть в состояние xk с вероятностью πjk (n) 0, то состояние xk
достижимо из состояния xi.
Два состояния xi и xk называются сообщающимися, если они достижимы друг из друга. Если два состояния не сообщаются, то либо πjk (n) 0, либо πkk (n) 0, либо оба условия выполняются одно-
временно [3].
Исходя из этих определений, все состояния можно разбить на классы эквивалентности по принадлежности к сообщающимся состояниям. Например, пусть процесс может находиться в пяти состояниях, и матрица переходных вероятностей имеет вид
65
0.3 |
0.7 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
0.4 |
0 |
0 |
0 |
|
|
π |
0 |
|
|
π 0 |
0 |
0 |
1 |
0 |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
0 |
π2 |
|
0 |
0 |
0.5 |
0 |
0.5 |
|
|
||||
|
|
|
|
|
|
|||||
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Матрица π распадается на два класса состояний: {1, 2} и {3, 4, 5}.Внутри класса состояния сообщающиеся, но классы между собой не сообщаются. В зависимости от реализации начального состояния переходные вероятности случайного процесса описываются либо подматрицей π1, либо подматрицей π2.
Цепь Маркова называется возвратной, если случайный процесс, выходящий из некоторого состояния xi, с вероятностью 1 возвращается в это же состояние xi когда-нибудь. В противном случае цепь называется невозвратной [4].
Множество возвратных сообщающихся состояний называется эргодическим. Если цепь состоит из единственного эргодического множества, она называется эргодической. При увеличении числа шагов n большего, чем n0, может случиться, что переходные вероятности не будут зависеть от начального состояния, т.е.
|
|
π |
1 |
|
|
|
|
π |
|
N |
|
πik (n n |
|
|
|
||
0) πk |
|
2 |
, |
πk 1. |
|
|
|
|
|
k 1 |
|
|
|
π |
|
|
|
|
|
|
N |
|
|
Цепь, удовлетворяющая этим условиям, называется регулярной эргодической цепью или стационарной цепью.
Распределение πk , k 1,2, ,N находится как решение системы линейных уравнений [3]
N |
|
πk i ik , |
k 1,2, ,N |
i 1 |
|
для некоторого n n0. |
|
66

Полученное распределение вероятности πk , k 1,2, ,K говорит о том, что распределение не зависит от начальных условий и исследуемая система переходит в стационарный режим
Если в матрице переходных вероятностей через n шагов содержится элемент, удовлетворяющий условию πik (n) δik, где δik - символ Кронекера, то состояние xi называется поглощающим.
Марковские процессы используются при решении практических задач, таких как, обнаружение сигналов, исследовании модели процесса рождения и гибели, в теории очередей, теории массового обслуживания.
2.7.5 Процесс Пуассона. Дробовой эффект
Под дробовым эффектом понимают «небольшое беспорядочное отклонение тока электровакуумных приборов и полупроводниковых приборов от среднего значения, вызванное неравномерностью электронной эмиссии или инжекцией носителей заряда в полупроводниковых приборах» [12].Предполагается, что демпферный (депрессия) эффект отсутствует. Рассмотрим дробовой эффект в электронных лампах[6]. Положим, T - время наблюдения, разделим интервал наблюдения на N интервалов длиной τ T/ N. Число N выберем таким большим, что вероятность вылета более одного электрона с катода была бы такой малой величиной, которой можно пренебречь. Тогда за время с катода вылетает один электрон с вероятностью p и не вылетает с вероятностью q 1 p. Положим, за время T с катода вылетело n электронов. Тогда величина тока в единицу времени рав-
на IT ne, где e - заряд электрона. (e 1.6 10-19 К). Среднее значе- T
ние тока равно
Iср M(IT) |
M(n) e |
|
pNe |
n1 e |
(2.68) |
T |
|
||||
|
|
T |
|
||
Величина n1 pN - среднее число электронов, вылетающих с ка- T
тода в единицу времени. Из этого соотношения получим
|
n1 |
N |
τ. Как видим, с уменьшением |
уменьшается и ве- |
|
p |
|
|
n1 |
||
|
|
||||
|
T |
|
|
||
роятность вылета электрона.
67

Интенсивность флюктуаций тока (дисперсия тока) равна
|
D(n) e2 |
|
pqNe2 |
|
e2 n1 |
|
n1 T |
|||
D(IT) |
|
|
|
|
|
|
|
(1 |
|
) |
T |
2 |
T |
2 |
T |
|
|||||
|
|
|
|
N |
||||||
С увеличением числа разбиений N (N ) дисперсия стремится к величине
D(IT ) |
e |
2 n1 |
|
eIср |
(2 69) |
|
T |
T |
|||
|
|
|
|
Введем относительное квадратичное отклонение
D(IT ) |
|
e |
(2.70) |
|
M(IT ) 2 |
T Iср |
|||
|
|
Из выражений (2.69) и (2.70) видно, что с увеличением времени наблюдения T дисперсия (флюктуации) и относительное квадратичное отклонение уменьшаются. За время T среднее число электронов, вылетевших с катода, равно n n1 T и будем считать это число электронов постоянным, не зависящим от N, т.е. с ростом N величина n не меняется. Тогда вероятность вылета одного электрона в каждом
временном интервале τ будет равна p1 n . Определим вероятность
N
PN(n) вылета n электронов во всех N интервалах:
P (n) Cn |
pn (1 p )N n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
N |
N |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N n |
|
|
|
|
|||||||||
|
N(N 1) (N (n 1)) |
n |
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
N |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
n |
n N(N 1) (N (n 1)) |
|
|
|
|
n |
|
|
|
N n |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Nn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
n |
n |
|
1 |
|
|
n 1 |
|
|
|
n |
|
|
|
|
N |
|
|
n |
|
n |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
. |
|||||||||||||||
|
|
|
N |
|
|
|
N |
N |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
n! |
|
N |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Определим вероятность PN(n) при N . Тогда, используя замену k N/n, имеем
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
k |
|
n |
|
|
|
|
|
|
|
|
|
|
nn |
|
n |
|
|
nn |
|
1 |
|
|
|
nn |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
n |
. |
||||||||||||||||||||
P(n) |
|
lim 1 |
|
|
|
|
|
|
|
|
lim |
|
1 |
|
|
|
|
|
|
|
e |
|
|
|||||
|
|
|
|
|
|
|
k |
|
|
|
||||||||||||||||||
|
|
n! N |
N |
|
|
n! k |
|
|
|
|
|
|
n! |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68

Таким образом, если известно среднее количество электронов n, вылетевших с катода за время T, то вероятность вылета n электронов за время T подчинено закону Пуассона
P(n) |
n |
n |
e |
n |
(2.71) |
|
|
||||
|
n! |
|
|||
Из вывода формулы (2.71) видно, что закон Пуассона применим к процессам, для которых вероятность появления интересующего события близка к нулю или единице и известно среднее количество событий n за время наблюдения T. Характерной особенностью закона Пуассона является равенство математического ожидания числа событий и дисперсии числа событий. Действительно,
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|||||
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||||||
M(n) n |
|
e |
|
|
|
|
e |
|
|
|
|
|
|
|
e |
|
e |
|
|
|
, |
||||||||||
|
n |
n |
n |
|
|
|
n |
n |
n |
n |
|||||||||||||||||||||
|
|
|
(n 1)! |
||||||||||||||||||||||||||||
n 0 |
|
n! |
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
M(n2) n2 |
|
e |
|
|
|
|
(1 |
|
|
|
|
|
|
||||||||||||||||||
|
n |
|
n |
n), |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
n 0 |
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
D(n) M(n2) (M(n))2 |
|
n |
. |
|
|
|
|||||||||||||||||||||||
3.Преобразование случайных процессов
влинейных инерционных цепях
Радиотехнические цепи можно разделить на линейные и нелинейные цепи, которые в свою очередь подразделяются на инерционные и неинерционные. Работа цепи может быть описана некоторым оператором. Оператор L, преобразующий входной процесс x(t) в выходной процесс y(t), называется линейным, если выполняется следующее условие
L(αx1(t) βx2(t)) αL(αx1(t)) βL(x2(t))
где α и β - константы.
Примерами линейных операторов являются дифференцирование, интегрирование, суммирования и т.д.
Если значение сигнала на выходе цепи в момент времени t определяется только лишь значением входного сигнала в тот же момент времени t, такая цепь называется неинерционной или системой без памяти. Если же значение сигнала на выходе цепи в момент времени
69

t определяется значением входного сигнала в момент времени t и реакцией цепи на сигналы, поданные в более ранние моменты вре-
мени, такая цепь называется инерционной или системой с памятью.
Инерционность цепи характеризуется постоянной времени цепи. Анализ радиотехнических цепей с точки зрения прохождения слу-
чайных процессов заключается в определении вероятностных характеристик на выходе цепи, если известны соответствующие характеристики на входе цепи и описание самой цепи.
Наиболее сложными для анализа являются нелинейные инерционные цепи. Для них нет общих методов анализа. В каждом частном случае нелинейного преобразования применяют тот метод, который позволяет решить задачу.
При анализе нелинейных неинерционных цепей, если не удается найти обратное преобразование, часто применяют кусочно-линейную аппроксимацию функции, описывающей работу цепи. Затем рассчитывают характеристики выходного сигнала на отдельных интервалах аппроксимации.
Определение функции распределения вероятности или плотности распределения вероятности при анализе линейных инерционных цепей довольно трудная задача. Поэтому ограничимся расчетами числовых характеристик на выходе линейной инерционной цепи. При этом применяются или аппарат дифференциальных уравнений, или импульсные характеристики, или передаточные функции (метод частотных характеристик).
Аппарат дифференциальных уравнений используется, когда анализируют как динамический (нестационарный) режим работы цепи, так и установившийся (стационарный) режим, начальные условия – произвольные.
Импульсными характеристиками удобно пользоваться, когда анализируют как динамический, так и установившийся режимы, но при нулевых начальных условиях.
Передаточные функции используются при анализе установившегося (стационарного) режима работы цепи.
(t) |
|
|
|
d |
(t) |
Применение дифференциальных урав- |
|||
|
|
|
|
|
|
|
|
|
нений. Пусть исследуемая цепь описывает- |
|
|
|
|
|
dt |
|
|||
|
|
|
|
|
|
ся известным дифференциальным уравне- |
|||
|
|
|
|
|
|
|
|
|
нием с постоянными коэффициентами, а на |
|
|
Рис. 3.1 |
|
||||||
|
|
|
вход цепи подается случайный сигнал ξ(t), |
||||||
70

(Рис.3.1). Тогда входной сигнал и выходной сигналы η(t) связаны соотношением
|
|
|
k |
|
djξ(t) |
|
|
|
m |
|
|
diη(t) |
|
|
|
(3.2) |
||||
a0 ξ(t) |
|
ai |
|
|
|
|
b0 |
η(t) |
|
bi |
dti |
|
|
|
||||||
|
|
|
|
dtj |
|
|
|
|
|
|
|
|||||||||
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
с начальными условиями |
|
|
|
|
dm 1η(t0) |
|
|
|
||||||||||||
η(t |
|
|
) C |
|
, |
dη(t0) |
C |
, , |
C |
|
. |
|||||||||
|
|
|
|
|
|
|||||||||||||||
|
0 |
|
|
|
0 |
|
|
dt |
1 |
|
|
|
|
dtm 1 |
|
m 1 |
|
|||
Предполагается, что условия дифференцируемости и интегрируемости случайных процессов выполнены. Применим оператор математического ожидания к обеим частям равенства (3.2)
|
|
|
k |
|
|
|
djMξ(t) |
|
|
m |
|
|
|
|
diMη(t) |
|||||
a0 Mξ(t) |
|
ai |
|
|
|
b0 η(t) |
|
bi |
|
|
. |
|||||||||
|
dtj |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dti |
|||||||
|
|
|
j 1 |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t) |
C |
|
|
|
|
(t) |
(t) |
R |
|
|
|
|
(t) |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.2
В результате получили обыкновенное дифференциальное уравнение с постоянными коэффициентами относительно Mη(t).
Рассмотрим примеры: прохождение случайного процессаξ(t) через интегрирующую и дифференцирующую цепи, (Рис.3.2).
Дифференциальные уравнения, описывающие интегрирующую и дифференцирующую цепи, соответственно имеют вид
1 |
ξ(t) |
dη(t) |
|
1 |
η(t), η(0) 0, |
(3.3) |
|||||
RС |
|
|
|
|
|||||||
|
|
|
dt |
|
|
RC |
|
||||
dξ(t) |
|
dη(t) |
|
1 |
|
η(t), η(0) 0. |
|
||||
|
|
|
|
|
|
||||||
dt |
|
|
dt |
RC |
|
||||||
Рассмотрим более подробно интегрирующую цепь. Решение уравнения (3.3) имеет вид
71
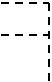
t |
|
|
η(t) αe α t ξ(x)eα xdx, где |
α 1/(RС). |
(3.4) |
0 |
|
|
Положим, M(ξ(t)) mξ. Вычислим математическое ожидание:
t |
|
M(η(t)) αe αt M(ξ(x))eα xdx mξ (1 e α t ) |
(3.5) |
0 |
|
Как видно из (3.5), математическое ожидание случайного процесса η(t) зависит от времени, т.е. процесс на выходе интегрирующей цепи – нестационарный даже если процесс на входе – стационарный. Но если время наблюдения t намного больше постоянной времени
цепиτ RC, |
то величиной |
e αt можно пренебречь и, |
в результате, |
|||||||||
получим |
|
|
|
M(η(t)) M(ξ(t)) mξ. |
|
|
(3.6) |
|||||
|
|
|
|
|
|
|
||||||
Вычислим корреляционную функцию процесса η(t): |
|
|
||||||||||
|
Bη(t1,t2) M(η(t1),η(t2)) |
|
|
|
|
|
|
|||||
|
|
|
|
t1 t2 |
|
|
|
|
|
|
|
|
|
α2 e α(t1 t2) M(ξ(x1)ξ(x2))eα(x1 x2)dx1 dx2 . |
|||||||||||
|
|
0 0 |
|
|
|
|
|
|
|
|
||
Если процесс ξ(t) - стационарный, то |
|
|
|
|
|
|
||||||
|
|
|
|
B (t1,t2) |
|
|
|
|
|
|
||
|
x2 |
|
|
|
t1t2 |
|
|
|
|
|
|
|
|
|
|
2 |
e (t1 t2) B(x2 |
x1)e (x1 x2)dx1 dx2. |
|||||||
t2 |
|
|||||||||||
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
Если процесс ξ(t) |
- белый шум с нулевым |
|||||||
|
|
|
математическим ожиданием, то |
|
|
|
||||||
|
|
x1 |
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
N0 |
α2 |
α(t t |
|
) |
|
||
|
|
|
|
|
|
|||||||
|
t1 |
|
|
|
Bη(t1,t2) |
|
|
e |
1 |
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
||
Рис. 3.3 |
t1 t2 |
|
|
|
δ(x2 x1)e |
α(x1 |
x2)dx1 dx2 . |
||
|
||||
|
0 0 |
|
|
При вычислении двойного интеграла необходимо учитывать свойства δ-функции и области интегрирования (0,t1) ,(0,t2), которые могут не совпадать.
72
