
Случайный процесс
.pdf
с коэффициентами ковариации
Rij |
M( (ti) m i ) ( (tj) m j) |
|
, |
|
(2.13) |
||
i |
j |
|
|||||
|
|
|
|
|
|||
математическим |
ожиданием |
mξi Mξ(ti ) |
|
и |
дисперсией |
||
σξ2i Dξ(ti), |
|
|
|
|
|
|
|
Di j - алгебраическое дополнение к элементу |
Rij |
ковариационной |
|||||
матрицы R.
Введем матрицу K с элементами Ki j i j Ri j, тогда совмест-
ная плотность распределения вероятности (2.6) запишется как
|
|
|
|
|
1 |
|
|
|
||
wξ (x1, ,xm, t1, ,tm) |
|
|
|
|
||||||
|
|
|
||||||||
2π n / 2 DetK |
||||||||||
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
1 |
(X Mξ(t))), |
(2.14) |
||||
exp( |
||||||||||
(X |
Mξ (t))K |
|
||||||||
2 |
|
|
|
|
|
|
|
|
||
где X (x1, ,xn ) (x(t1), ,x(tn )) |
- транспонированный вектор |
|
значений случайного процесса в дискретные |
моменты времени |
|
t1, ,tn , |
|
|
|
, ,mξn ) |
- транспонирован- |
Mξ (t) Mξ(t1), ,Mξ(tn ) (mξ1 |
||
ный вектор значений математического ожидания в дискретные моменты времени t1, ,tn ,
DetK - определитель матрицы K.
В частности, одномерная и двумерная плотности распределения вероятности имеют вид
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x mξ(t) 2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
wξ (x, t) |
|
|
|
|
|
e |
2σξ2 |
(t) |
, |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2π σξ (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
wξ (x1,x2,t1,t2) |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2πσξ1 σξ 2 1 r2 |
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
(x1 |
m |
ξ1) |
2 |
|
|
(x1 mξ1) (x2 |
mξ2) |
|
(x2 m |
ξ2) |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||||
exp |
|
|
|
|
|
|
|
|
|
|
|
2r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2(1 r |
|
|
σ2 |
|
|
|
|
|
|
σξ1 |
|
|
|
|
σξ2 |
σ |
2 |
|
|
||||||||||||
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
ξ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ2 |
|
|
|
|
|
где mξi mξ (ti), σξi σξ (ti), i 1, 2, r R12 R21 r(t1,t2).
43

Положим, процесс ξ(t) - стационарный хотя бы в широком смысле. Тогда коэффициент корреляции равен r r(t2 t1) и двумерная плотность распределения вероятности примет вид
wξ (x1, x2, t2 t1) w |
ξ (x1, x2, τ) |
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
2πσ2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 r2 |
|
|
||||||||
|
|
|
1 |
|
|
(x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
m) |
2r(x |
|
m)(x |
|
m) (x |
|
m) |
|
|||||||||
exp |
|
2 |
|
2 |
|
1 |
|
1 |
2 |
2 |
|
. (2.15) |
|||||||||||
|
2σ |
(1 r |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если значения стационарного случайного процесса не коррелированны, то корреляционный момент равен нулю и плотность распределения вероятности равна
wξ (x1, ,xn, t1, ,tn )
|
1 |
|
|
|
1 |
|
n |
|
n |
|
|
|
|
|
(xi mξ ) |
2 |
wξ (xi,ti). (2.16) |
||
|
|
|
exp |
|
|
|
|
||
2 |
n / 2 |
2σ |
2 |
||||||
|
(2πσξ ) |
|
|
|
ξ i 1 |
|
i 1 |
||
Если нормальный случайный процесс стационарен в широком смысле, то он будет стационарным и в узком смысле. Покажем это. Из формулы (2.11) получим
wξ (x1, ,xn , t1, ,tn )
|
(2 )n/2 |
n |
D |
|
2 |
2 |
|
n |
n |
|
|
|
D |
|
|||||||
|
1 |
|
|
exp |
1 |
|
|
|
Di j(xi m ) (xj m ) . (2.17) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
i 1 |
j 1 |
|
||
Как видно из (2.6) и (2.17) совместная плотность распределения вероятности wξ (x1, ,xn , t1, ,tn ) зависит от нормированной ко-
вариационной матрицы R. Для стационарного процесса в широком смысле она будет равна
|
|
1 |
R(t1 t2) |
R(t1 |
tn ) |
|
||
|
|
|
t1) |
1 |
R(t2 |
|
|
|
R |
R(t2 |
tn ) |
(2.18) |
|||||
|
|
|
|
|
|
. |
||
|
|
|
|
|
||||
|
|
|
t1) |
R(tn t2) |
|
1 |
|
|
|
R(tn |
|
|
|||||
44
Если сдвинуть все точки отсчёта по времени на одну и ту же величину , (t1 , ,tn ), то элементы нормированной ковариаци-
онной матрицы не изменятся, и многомерная плотность распределения не будет зависеть от сдвига . Отсюда следует, если нормальный случайный процесс стационарен в широком смысле, то он будет стационарным и в узком смысле.
Как видно из выше изложенного, нормальный случайный процесс содержит в качестве параметров математическое ожидание и ковариационную матрицу.
2.4 Каноническое разложение случайного процесса
Анализ случайных процессов при их прохождении через радиотехнические цепи бывает сложным из-за математических трудностей. На практике пользуются методами, упрощающими вычислительный процесс. Одним из этих методов является каноническое разложение случайного процесса.
Вводится элементарный случайный процесс ξ0(t) Vφ(t) , где V - случайная величина, φ(t) - не случайная функция времени,
называемая координатной функцией. Определим математическое ожидание и корреляционную функцию процесса ξ0(t):
Mξ0(t) mv φ(t), Bξ0 |
(t1,t2) M(ξ0(t1)ξ0(t2)) M(V2)φ(t1)φ(t2), |
|
ковариационная функция равна |
|
|
o |
o |
2) mv2 ) φ(t1)φ(t2). |
B o (t1,t2) M(ξ0(t1)ξ0(t2)) (M(V |
||
ξ0 |
|
|
Как видно из этих выражений, в общем виде элементарный случайный процесс не является стационарным хотя бы в широком смысле.
Представим случайный процесс ξ(t) через элементарные случайные процессы
N |
|
ξ(t) mξ (t) Vi φi(t), |
(2.19) |
i 1 |
|
где mξ (t) - не случайная функция, Vi - коэффициенты разложения – некоррелированные случайные величины с математическим ожида-
нием, равным нулю и дисперсией σ2vi :
45
0 |
|
|
при j i , |
|
|
|
|
|
(2.20) |
M(Vi Vj) D(V ) σ2 |
при j i . |
|||
|
i |
vi |
|
|
|
|
|
|
|
Множество координатных функций может быть как конечным, так и бесконечным. Представление случайного процесса в виде (2.19) с ограничениями (2.20) называется каноническим разложением слу-
о
чайного процесса. Для центрированного процесса ξ(t) ξ(t) mξ (t)
имеем
о |
N |
|
ξ(t) Vi φi(t). |
(2.21) |
|
i 1
Возможно интегральное представление
(t) m (t) V( ) (t, ) d , |
(2.22) |
где V(τ) - белый шум с математическим ожиданием M(V(τ)) 0, φ(t,τ) - неслучайная функция времени t и параметра τ.
Такое представление случайного процесса называется интеграль-
ным каноническим разложением.
Будем полагать в дальнейшем в этом разделе, что процесс ξ(t) -
o
центрированный, т.е. ξ(t) ξ (t), и выразим корреляционную функцию процесса ξ(t), используя каноническое разложение:
|
N |
N |
|
|
|
Vi φi(t1) Vj φj(t2) |
|
|
|
Bξ(t1,t2) M ξ(t1)ξ(t2) M |
|
|||
i 1 |
i 1 |
|
|
|
N |
N |
N |
φi(t1)φi(t2) |
|
M Vi Vj φi(t1)φj(t2) M Vi2 |
|
|||
i 1 |
j 1 |
i 1 |
|
|
|
|
N |
|
|
|
|
D Vi φi(t1)φi(t2) . |
(2.23) |
|
|
|
i 1 |
|
|
Разложение (2.23) называется каноническим разложением ковариационной функции. Дисперсия процесса ξ(t), выраженная через координатные функции, имеет вид
46
N |
φ i2(t1) . |
|
D(ξ) Bξ (t1 t2) D Vi |
(2.24) |
i 1
Доказано [7], если ковариационная функция случайного процесса ξ(t) имеет вид (2.23), то случайный процесс ξ(t) может быть представим в виде (2.21). На практике часто применяют это утверждение. Выбор координатных функций φi(t) зависит от свойств случайного процесса ξ(t) и набора известных случайных величин V1, V2 , , VN. Более подробно теория и практика канонического разложения случайной функции изложена в [7].
Рассмотрим стационарный случайный процесс ξ(t) в интервале (0, Tн). Корреляционная функция Bξ (τ) может быть представима разложением в ряд Фурье на интервале ( Tн τ Tн):
|
|
|
|
|
|
|
|
|
|
|
Bξ (τ) Bξ (t2 |
t1) D0 Di |
сos ωiτ , |
|
|||||||
|
|
|
|
i 1 |
|
|
|
|
||
|
|
|
|
|
π |
|
|
|||
D0 Di |
сos(ωi (t2 t1)), ωi iω0 i |
. |
(2.24) |
|||||||
|
||||||||||
i 1 |
|
|
|
|
|
Tн |
|
|||
Коэффициенты разложения определяются как |
|
|
|
|
||||||
|
|
|
|
1 |
Tн |
|
|
|
|
|
|
|
|
D0 |
Bξ (τ) dτ, |
|
|
|
(2.25) |
||
|
|
|
2T |
|
|
|
||||
|
|
|
|
н |
T |
|
|
|
|
|
|
|
|
Tн |
|
н |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
Di |
Bξ (τ) сosωiτdτ, i 1,2, , |
(2.26) |
||||||||
T |
||||||||||
|
|
н T |
|
|
|
|
|
|
||
|
|
|
н |
|
|
|
|
|
|
|
Перепишем выражение (2.24) в виде
Bξ (t2 t1) D0 Di сos(ωi (t2 t1))
|
i 1 |
|
|
D0 Di |
сosωit1 сosωit2 Di sinωit1 sinωit2 . (2.27) |
i 1 |
i 1 |
В результате получили разложение ковариационной функции случайного процесса ξ(t) по координатным функциям cosωit и sinωit на интервале ( Tн,Tн). Ввиду взаимной однозначности представле-
47
ния канонического разложения случайного процесса ξ(t) и его ковариационной функции имеем
|
|
|
ξ(t) U0 Ui cosωit Vi sinωit, |
(2.28) |
|
i 1 |
i 1 |
|
где U0, Ui, Vi - не коррелированные случайные величины с математическими ожиданиями и дисперсиями соответственно
M(U0) M( Ui) M(Vi) 0 ,
D(U0) D0, D( Ui ) D(Vi ) Di.
Представление (2.28) называется спектральным разложением случайного процесса ξ(t) на интервале (0,Tн). Наличие случайной величины U0 свидетельствует о том, что процесс ξ(t) не является эргодическим, так как нарушается условие эргодичности Слуцкого. Если коэффициент D0 в (2.28) будет равен нулю, то процесс ξ(t) будет эргодическим.
2.5 Квазидетерменированный случайный процесс
Случайный процесс ξ(t, A, , ) называется квазидетерменированным, если он описывается неслучайной функцией времени, содержащий в качестве параметра одну или несколько случайных величин с известными совместными плотностями распределения вероятности.
Случайность проявляется в том, что в момент начала отсчета случайные параметры принимают одно из своих возможных значений и в дальнейшем не изменяются во время наблюдения процесса, т.е. процесс в дальнейшем будет детерминированным. Многомерная плотность распределения вероятности зависит от распределения вероятности в момент t t1. Выразим многомерную плотность распределения вероятности квазидетерменированного процесса через одномерную плотность и условную плотности распределения вероятности:
wξ (y1, , yn , t1, tn )
wξ (y1, t1) wξ (y2, , yn , t2, tn / y1, t1) (2.29)
48
Положим, что найдена одномерная плотность распределения wξ (y1, t1). Ввиду того, что значения случайных величин в моменты
времени t2, tn известны и неизменны, то можно использовать - функцию для описания условной плотности распределения wξ (y2, , yn, t2, tn / y1, t1):
|
n |
|
wξ (y2, , yn, t2, tn / y1, t1) δ(yi Q(ti / y1, t1)), |
||
где Q(ti / y1, t1) |
i 2 |
|
- функция, описывающая процесс ξ(t) |
в моменты |
|
времени t t2 при условии, что значение процесса в момент t t1 |
||
известно. |
|
|
Пример 2.1. |
Случайный процессξ(t) Aсos( t ) |
содержит |
случайные величины амплитуду A, частоту |
и фазу , не завися- |
|
щие от времени. Для простоты будем считать |
амплитуду A случай- |
|
ной величиной |
с известной плотностью распределения wA(x), |
|
x1 x x2, а |
частоту и фазу будем считать известными, т.е. |
|
ω, 0, ξ(t) Acosωt. Случайный процесс принимает значе- |
||
ния y(t) xcosωt. В момент времени |
|
t t1имеем y(t1) xcosωt1, и |
||||||||||||||||||||||||||||||
амплитуда сигнала будет равна |
|
x |
|
y(t1) |
. Одномерная плотность |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosωt1 |
|
|
|
|
|
|
|
|
|
|||||
распределения wξ(y1, t1) будет равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
w |
(y , t |
1 |
) w |
A |
( |
y1 |
|
) |
|
dx |
|
w |
A |
( |
y1 |
) |
|
1 |
|
|
. |
|||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
ξ 1 |
|
|
cos ωt |
1 |
|
|
|
|
dy |
|
|
|
cos ωt |
1 |
|
|
cos ωt |
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Функция Q(ti / y1, t1) равна: |
|
y(t1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Q(t |
|
/ y , t |
|
) |
|
|
|
|
cosωt |
|
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
cosωt1 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
i |
1 |
|
|
1 |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
||||||
Таким образом, многомерная плотность распределения примет вид w(y1, ,yn ,t1, ,tn )
|
y(t1) |
1 |
|
|
n |
y(t1) |
||||
|
|
|
δ(yi |
|||||||
wA ( |
|
) |
|
|
|
|
|
|
cosωti ). |
|
cosωt1 |
|
|
cosωt1 |
|
|
cosωt1 |
||||
|
|
|||||||||
|
|
|
|
|
|
|
|
i 2 |
|
|
|
|
|
|
|
|
|
|
|
||
2.6 Узкополосный случайный процесс По свойствам спектральной плотности мощности случайные про-
49
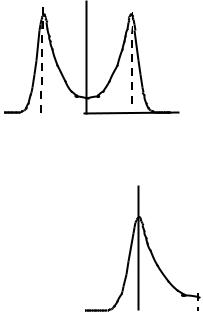
цессы могут быть разделены на широкополосные и узкополосные.
Случайный процесс ξ(t) называется узкополосным, если его спектральная плотность мощности сосредоточена вблизи какой-либо частоты, (Рис 2.1). Другими словами, узкополосный процесс характеризуется полосой частот ω0, в пределах которой сосредоточена основная мощность процесса по отношению к частоте ω0, т.е. признаком узкополосности процесса является соотношение
ω ω0.
Определим ковариационную функцию процесса, исходя из определения. Считаем, что спектральная плотность мощности F(ω) известна
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B(τ) |
|
|
F(ω)exp( jωτ)dω. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перейдем к полосе частот в преде- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
- 0 |
|
|
0 |
|
0 |
|
|
|
лах (0, ) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
F( ) |
|
|
|
|
|
|
B(τ) |
|
F0(ω)сosωτ dω |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сделаем зеркальное отображение спек- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
тральной плотности мощности по от- |
||||||||||||
|
|
-∞ |
|
|
|
|
|
|
|
|
|
ношению к точке ω0 и переместим на- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
чало координат в точку ω0 |
при |
|
||||||||||||
|
|
|
|
|
|
|
0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
помощи преобразования ν ω0 ω, |
|||||||||||||||
|
|
|
|
Рис. 2.1 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(Рис. 2.1). Это преобразование позво- |
||||||||||||
ляет рассматривать спектральную плотность мощности в области |
|||||||||||||||||||||||||
низких частот. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
В результате получим |
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
B(τ) |
F0(ν)сos(ω0 ν)τ dν |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2π |
|
|
|
||||||||||||||
|
|
|
|
ω0 |
|
|
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
F (ν)сosντdν |
|
сosω |
|
τ |
|
F (ν)sinντdν sinω |
|
τ . |
|||||||||||||
|
|
|
0 |
|
0 |
||||||||||||||||||||
|
|
2π |
0 |
|
|
|
|
|
|
2π |
0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
50
Введем обозначения |
|
|
|
|
|
|
|
|||
|
ω0 |
|
|
|
|
|
ω0 |
|
|
|
ac(τ) 2π1 F0(ν)cosντ dν; |
as(τ) 2π1 F0(ν)sin ντ dν. |
(2.30) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
Функции ac(τ) и as(τ) - медленно меняющиеся функции времени, |
||||||||||
так как их спектры принадлежат низкочастотной области. |
|
|||||||||
В новых обозначениях имеем |
|
|
|
|
||||||
B(τ) ac(τ) cosω0τ as(τ) sinω0τ a(τ) cos(ω0τ φ(τ)), |
(2.31) |
|||||||||
где ac(τ) a(τ) cosφ(τ) , |
as(τ) a(τ) sinφ(τ),. |
|
|
|
||||||
|
aс(τ) |
2 |
as(τ) |
2 |
|
a |
s |
(τ) |
|
|
a(τ) |
, |
|
|
|
||||||
|
|
φ(τ) arctan |
|
. |
|
|||||
|
|
|
|
|
|
|
aс |
(τ) |
|
|
Как видно из (2.30) и (2.31), корреляционная функция узкополос- |
||||||||||
ного процесса является гармоническим колебанием с частотой ω0, |
||||||||||
модулированным низкочастотным сигналом a(τ), фаза гармониче- |
||||||||||
F( ) |
|
ского колебания φ(τ) зависит от τ. |
|
|||||||
|
|
|
|
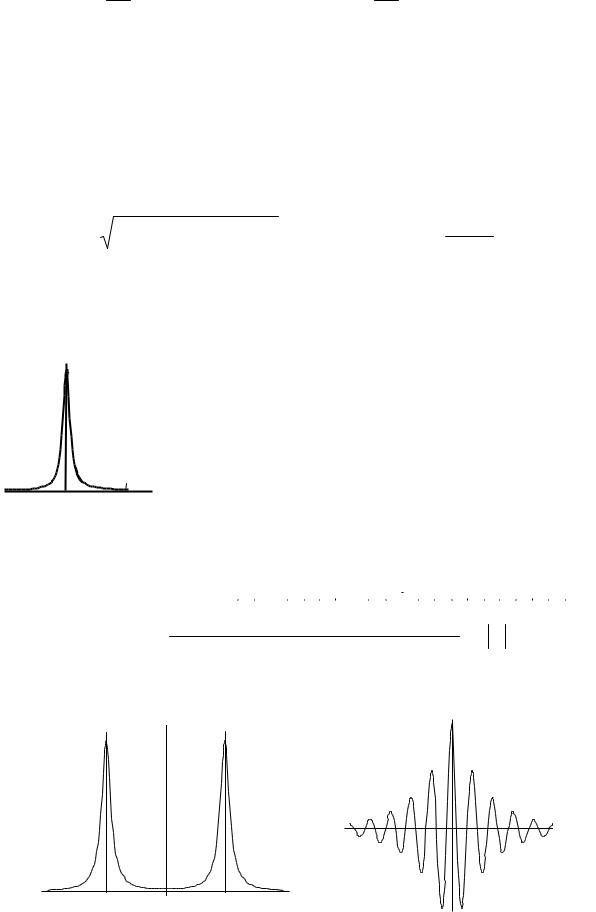
На практике обычно спектральная плотность |
||||||
|
|
|
мощности F(ν) бывает симметричной функци- |
|||||||
|
|
|
ей (Рис. 2.2). В этом случае, если пренебречь |
|||||||
|
|
|
мощностью процесса в области (ω0, ), синус- |
|||||||
0 |
0 |
|
ная составляющая as(τ) обратится в нуль и по- |
|||||||
Рис. 2.2 |
|
|
лучим простое выражение B(τ) ac(τ) сosω0τ. |
|||||||
|
|
|
|
В частности, если спектральная плотность |
||||||
мощности определяется как (Рис 2.3а , f0 50 Гц, |
30 1/Сек) |
|||||||||
|
|
|
|
2α(α2 ω2 ω02) |
|
|
|
|||
|
F(ω) (α2 (ω ω0)2) (α2 (ω ω0)2), |
ω , |
|
|||||||
|
F( ) |
|
|
|
|
|
B( ) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
51 |
|
|
|
|||
|
Рис. 2.3а |
|
|
|
|
|
|
|||
|
|
|
|
Рис. 2.3б |
|
|||||
корреляционная функция случайного процесса имеет вид
B(τ) e α |
|
τ |
|
cosω |
0 |
τ, |
|
|
|||||
которая изображена на Рис. 2.3б. |
|
|||||
|
|
|||||
Представление корреляционной функции в виде (2.31) позволяет записать модель узкополосного процесса в виде
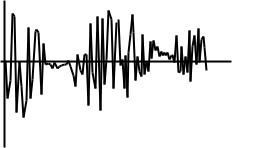
ξ(t) A(t)сos(ω0 t (t)), |
(2.32) |
где A(t) - огибающая узкополосного случайного процесса, является также случайным процессом, (t) - случайная фаза узкополосного случайного процесса.
Представим случайный процесс (2.32) в виде
ξ(t) A(t)сos (t)сosω0 t A(t)sin (t)sinω0t |
|
Ac(t)cosω0 t As(t)sinω0 t, |
(2.33) |
y(t)
Рис. 2.4
где |
Ac(t) A(t)cos (t), |
|
As(t) A(t)sin (t) |
(2.34) |
|
|
Одна из возможных реализаций уз- |
||
t |
кополосного |
случайного |
процесса |
представлена на Рис.2.4. |
|
||
|
|
||
|
Составляющие Ac(t) и |
As(t) яв- |
|
|
ляются медленно меняющимися функ- |
||
|
циями по сравнению с |
функциями |
|
сosω0t и sinω0t.
Рассмотрим плотность распределение вероятности огибающей A(t) и фазы (t) узкополосного процесса. Положим косинусная Ac(t) и синусная As(t) составляющие являются стационарными случайными процессами хотя бы в широком смысле, взаимно независимы и распределены по нормальному закону с соответствующи-
ми |
математическими |
ожиданиями (mc, ms ) |
и |
|
дисперсиями |
|||||||||||||||||||
σс2 σs2 σ2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
x |
c |
m |
c |
2 |
|
x |
s |
m |
s |
2 |
|
||||
w |
(x |
c |
,x |
s |
) |
|
|
exp |
|
|
|
|
|
|
|
|
|
|
|
, (2.35) |
||||
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|||||||||||
|
Ac,As |
|
|
2πσ |
|
|
|
|
2σ |
|
|
|
|
|
2σ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
xc(t) x(t)cosφ(t) f1, |
|
|
|
xs(t) x(t)sinφ(t) f2. |
|||||||||||||||||||
52
