
Случайный процесс
.pdf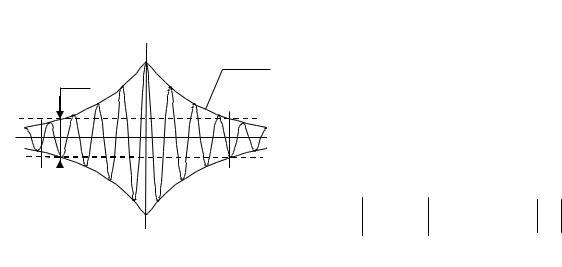
6. На практике необходимо знать интервал времени , в пределах которого нельзя пренебречь зависимостями между значениями случайного процесса. Этот интервал называется интервалом корреляции. Реализации, отстоящие по времени больше, чем интервал корреляции, считаются некоррелированными. Интервал корреляции может быть определен несколькими способами.
1) Площадь под кривой нормированной корреляционной функции Rξ (τ) равна площади прямоугольника с основанием, равным 2 τ, и
высотой, равной единице (Рис. 1.9)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bξ (τ) dτ |
|
|
|
|
|
|
|
(1.12) |
||
|
|
τ |
|
|
|
|
|
|
|
|
|||
|
|
|
2 Bξ (0) |
|
|
|
|
|
|
|
|
|
|
2)Введем |
R*(τ) |
- |
огибающую нормированной корреляционной |
||||||||||
|
R( ) |
|
функции и ρ - допустимый коэф- |
||||||||||
|
* |
фициент |
|
корреляции, |
|
0 ρ 1, |
|||||||
|
|
|
выбранный |
из практических |
со- |
||||||||
2 ρ |
|
|
R ( ) |
ображений. Будем считать, (Рис. |
|||||||||
|
|
|
|||||||||||
|
|
|
|
1.10), |
значения |
процесса |
ξ(t) |
||||||
|
|
|
коррелированными на |
интервале |
|||||||||
|
|
|
|
времени |
τ, где |
τ выбрано из |
|||||||
- 0 |
|
|
0 |
решения равенства |
|
|
|
|
|||||
|
|
|
|
|
R*(τ |
0 |
) ρ: |
τ τ |
0 |
. |
|
||
Рис.1.10 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
Существуют и другие методы |
|||||||||||
|
|
|
|
определения интервала |
|
корреля- |
|||||||
ции.
Рассмотрим частный случай, когда время корреляции τ принимает дискретные значения
τ t2 t1 k t. Установим связь между значениями коэффициента корреляции Rξ(τ) B0ξ(τ)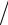 B0ξ(0) случайного процесса ξ(t) и коэф-
B0ξ(0) случайного процесса ξ(t) и коэф-
фициентом корреляции Rij системы случайных величин ξ1,ξ1, ,ξn ,
распределенных по одному и тому же закону с одинаковыми матема-
тическими ожиданиями m и одинаковыми дисперсиями σ2. Коэффициент корреляции Rij является элементом корреляци-
онной матрицы
13

|
|
1 |
R12 |
R1n |
|
|
||
|
|
|
1 |
|
|
|
|
|
R |
R21 |
R2n |
(1.13) |
|||||
|
|
|
|
|
|
|||
|
|
|
|
|||||
|
|
|
Rn2 |
|
1 |
|
|
|
и вычисляется как |
Rn1 |
|
|
|||||
|
M (ξi m)(ξj m) |
|
|
|||||
|
|
|
|
|||||
Rij |
|
|
|
|
. |
|
(1.14) |
|
|
σ2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
Рассмотрим случайный процесс ξ(t) в дискретные моменты времени ti и пусть i 0,1, ,n 1. Так как ковариационная функция процесса ξ(t) рассматривается в дискретные моменты времени и на конечном интервале времени, равном n t, коэффициент корреляции случайного процесса ξ(t) удобно представить через корреляционную
матрицу
R(Δt)
|
|
1 |
|
R( t) |
R(2 t) |
R((n 1) t) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R( t) |
|
1 |
R( t) |
|
R((n 2) t) |
(1.15) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
R((n 2) t) |
R((n 3) t) |
|
1 |
|
|
|||
|
R((n 1) t) |
|
|
|||||||||
где |
R(k t) |
M[(ξ(t2) m)(ξ(t1) m)] |
, |
t2 |
t1 |
k. |
|
|
||||
|
σ2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
корреляционных матриц R и |
|||||
Сравнивая элементы Rij и |
R(k t) |
|
||||||||||
R( t), видно, что Rij R( i j t), т.е. значения коэффициента кор-
реляции случайного процесса ξ(t) в дискретные моменты времени совпадают со значениями коэффициента корреляции системы случайных величин ξ1,ξ1, ,ξn , если τ i j t.
1.4. Характеристическая функция случайного процесса
Свойства случайного процесса можно описать не только плотностью распределения вероятности и функцией распределения вероятности, но и с помощью характеристической функции.
Рассмотрим случайную величину ξ, имеющую плотность распре-
14

деления вероятности wξ(x) для непрерывной случайной величины и распределение вероятности P(ξ xk) pk , k 1,2, для дискрет-
ной случайной величины. Характеристической функцией θξ(v)слу-
чайной величины |
ejvξ |
|
называется математическое ожидание слу- |
||||||
чайной величины ejvξ: |
|
|
|
||||||
|
|
|
|
|
|
ξ |
|
|
|
|
|
|
|
|
|
w |
(x) ejvx dx для непрерывных сл. в. |
||
|
|
|
|
|
|
|
|||
θ |
|
(v) M(e |
jvξ |
|
|
|
|
|
(1.16) |
|
|
) |
|
|
|||||
|
ξ |
|
|
pk |
ejvxk для дискретных сл.в., |
||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где v - произвольный вещественный параметр, j 
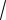 1. Обратное преобразование имеет вид
1. Обратное преобразование имеет вид
|
21π |
|
wξ (x) |
θξ (v) e jv x dv . |
Приведем некоторые свойства характеристической функции случайной величины.
1. θξ(v) 1. Действительно,
|
|
|
|
|
|
|
θξ(v) |
|
|
wξ(x) ejvx dx |
|
wξ(x) ejvx dx |
wξ(x) dx 1. |
|
||||||
|
||||||
|
|
|
|
|
|
|
2. θξ (0) 1, следует из определения характеристической функции.
|
|
|
3. θξ (v) |
wξ (x) cos(vx)dx j wξ (x) sin(vx)dx. |
|
|
|
|
4. θξ ( v) θξ (v) следует из пункта 3, где θξ (v) - функция , ком-
плексно сопряжённая функции θξ (v).
5. lim θξ (v) 0. Доказательство этого свойства приведено в [5]
v
6. Если плотность распределения вероятности wξ (x) симметрич-
ная функция, то характеристической функции θξ (v) - действительная четная функция
15
|
|
(v) |
w (x) cos vxdx. |
7. Если характеристическая функция θξ (v) - действительная чет-
ная функция, то плотность распределения вероятности wξ (x) - сим-
метричная функция.
Одним из удобств применения характеристической функции является легкость нахождения моментов распределения вероятности. Продифференцируем θξ (v):
dkθξ (v) |
|
|
|
xk wξ (x) ejvx dx . |
|
||
|
jk |
(1.17) |
|
dvk |
|||
|
|
|
|
Из этого выражения получим моменты k-го порядка:
|
k |
1 |
|
k |
θξ (v) |
|
|
||
Mξ |
d |
|
|
mξ k. |
|||||
|
|
|
|
|
|
|
|
||
|
jk |
dvk |
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
v 0 |
|
|
Если существуют моменты любого порядка, то разложение характеристической функции в ряд Тейлора в точке v 0 имеет вид
θξ (v) 1 |
|
mξk |
(jv)k |
(1.18) |
k 1 |
|
|||
|
k! |
|
||
На практике часто приходится сталкиваться с поиском функции и плотности распределения вероятности суммы независимых случайных величин ξi с известными характеристическими функциями θξi (v). Согласно определению (1.16) характеристическая функция
суммы независимых случайных величин равна произведению характеристических функций, т.е.
n |
n |
θξ (v) M(ejvξ ) M(ejv in 1ξi ) M(ejvξi ) θξi (v). (1.19) |
|
i 1 |
i 1 |
Формула (1.15) позволяет вычислить плотность распределения вероятности суммы независимых случайных величин.
Другой функцией, которая характеризует моменты случайной величины, является кумулянтная функция. Кумулянтной функцией случайной величины ξ называется логарифм характеристической функции
16
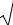
ψ(v) lnθξ (v). |
(1.20) |
Кумулянтная функция может быть разложена ряд по степеням v в точке v0 0. Для этого рассмотрим разложение функции ln(1 z) в ряд Тейлора в точке z0 0:
|
z2 |
|
z3 |
|
z4 |
|
k 1 zk |
|
|
ln(1 z) z |
|
|
|
|
|
k 1( 1) |
|
|
. (1.21) |
2 |
3 |
4 |
|
k |
|||||
Сделаем подстановку z θξ (v) 1 и получим, используя (1.18) и (1.21),
|
mξk |
|
|
|
1 |
|
|
mξk |
|
2 |
|
||
ψξ (v) |
|
|
(jv) |
k |
|
|
|
|
|
|
(jv) |
k |
|
|
|
|
|
|
|||||||||
k 1 k! |
|
2 |
|
k 1 k! |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
1 |
|
mξk |
|
3 |
|
1 |
|
|
mξk |
|
4 |
|
|||||
|
|
|
|
|
|
|
(jv) |
k |
|
|
|
|
|
|
(jv) |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
k 1 k! |
|
|
|
4 |
|
|
k 1 k! |
|
|
|
||||
Возведя в соответствующие степени выражения в круглых скобках и собрав все члены с одинаковыми степенями относительно членов jv, получим степенной ряд вида
ψ(v) |
χk |
(jv)k , |
(1.22) |
|
|||
k 1 k! |
|
||
где коэффициенты разложения χk , называемые кумулянтами (семиинвариантами), являются полиномами от моментов mξk , k 1,2,3,
В частности
o
χ1 mξ1, χ2 mξ2 m2ξ1 M(ξ)2 Dξ,
χ |
|
m |
|
3m |
|
m |
|
2m |
3 |
o |
3, |
χ |
|
o |
4 |
o |
2 ) |
2 (1.23) |
3 |
ξ3 |
ξ1 |
ξ2 |
M(ξ) |
4 |
M(ξ) |
3(M(ξ) |
|||||||||||
|
|
|
|
|
ξ1 |
|
|
|
|
|
|
|
|
Пример 1. Пусть случайная величина ξ распределена по нормаль-
ному закону с математическим ожиданием mξ и дисперсией σξ2, N m , 2 :
1 |
|
|
|
(x mξ )2 |
|
|
||||
|
|
|
|
|||||||
w(x) |
|
|
|
|
exp |
|
|
, |
x |
. |
|
|
|
|
|
2 |
|||||
|
|
2π σ |
ξ |
|
2σ |
|
|
|
||
|
|
|
|
|||||||
|
|
|
|
|
|
ξ |
|
|
|
|
Характеристическая функция случайной величины ξ имеет вид
17

|
1 |
2 |
2 |
|
|
jvmξ |
|
σξ v |
|
|
|
|
||
θξ (v) e |
2 |
|
, |
|
|
|
|
||
а кумулянтная функция –
ψξ (v) jvmξ 1σξ2 v2. 2
Пример 2. Рассмотрим сумму трех независимых нормально распределенных случайных величин ξ ξ1 ξ2 ξ3, математические ожидания и дисперсии которых соответственно равны mξ1, mξ2 , mξ3,
σξ21, σξ22, σξ23. Определим плотность распределения вероятности wξ (x).
Характеристические функции случайных величин ξi равны соответственно
|
1 |
2 |
2 |
|
|
jvmξi |
|
σξi v |
|
|
|
|
||
θξi (v) e |
2 |
|
|
|
|
|
|
|
|
По формуле (1.19) вычислим характеристическую функцию случайной величины ξ
|
|
3 |
|
1 |
2 |
2 |
|
|
3 |
v2 |
3 |
2 |
θξ (v) exp |
i 1 |
(jvmξi |
|
σξi v |
|
) |
exp jv i 1mξi |
|
i 1 |
σξi . |
||
2 |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Введем обозначения mξ 3i 1mξi, σ2ξ 3i 1σ2ξi .
Тогда характеристическая функция суммы случайных величин равна
|
1 |
2 |
2 |
|
|
jvmξ |
|
σξ v |
|
|
|
|
||
θξ (v) e |
2 |
|
. |
|
|
|
|
||
Но полученная формула представляет характеристическую функцию нормально распределенной случайной величины с параметрами mξ,σ2ξ .
Для многомерных случайных величин ξ1, ξn можно также записать характеристическую функцию
|
|
|
|
n |
|
|
θ |
(v , ,v |
|
|
j vi ξi |
|
|
n |
) M e i 1 |
|
||||
|
ξ 1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18

|
|
n |
|
x |
|
|
|
|
|
j v |
|
|
|
||
wξ (x1, ,xn ) e i 1 |
i |
|
i |
dx1 dxn |
(1.24) |
||
|
|
|
|
|
|
|
|
Соответственно можно записать совместную плотность распределения вероятности
|
|
|
|
|
n |
|
x |
|
|
|
|
1 |
|
|
j v |
|
|
||
wξ (x1, ,xn ) |
|
θξ (v1, ,vn ) e |
i 1 |
i |
|
i |
dv1 dvn (1.25) |
||
2 |
π n |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Определение и свойства характеристической функции перенесем на случайный процесс
θξ (v,t) M(ejvξ(t)) wξ (x,t) ejvx dx
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
θ |
(v , ,v |
|
,t |
|
, ,t |
|
) M |
|
j vi ξ(ti) |
|
||||
n |
1 |
n |
|
e i 1 |
|
|
|
|
||||||
|
ξ 1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
j v |
|
|
|
||
wξ (x1, ,xn ,t1, ,tn ) e i 1 |
i |
|
i |
dx1 dxn . |
||||||||||
(1.26)
(1.27)
Приведенные формулы позволяют исследовать свойства случайного процесса.
1.5. Дифференцирование и интегрирование случайного процесса
Понятие дифференцируемости и интегрируемости связано с непрерывностью функции. Для детерминированных функций функция f(t) непрерывна в точке t t0, если существует предел
lim f(t) f(t ). Однако такой критерий непрерывности для случай-
t t0 0
ного процесса непригоден, так как возможна не одна реализация, а целое множество реализаций для любого t.
Случайный процесс ξ(t) называется непрерывным в точке t, если при любом ε 0 можно найти такое δ 0, что
M |
ξ(t T) ξ(t) |
|
2 ε |
при |
|
T |
|
δ или |
|
|
|
19

lim M |
ξ(t T) ξ(t) |
|
2 0. |
(1.28) |
|
||||
T 0 |
|
|
|
|
|
|
Случайный процесс ξ(t), непрерывный во всех точках t ξ, где
ξ - область, в которой существует случайный процесс, называется непрерывным в области ξ .
Рассмотрим, как влияет понятие непрерывности на математическое ожидание и ковариационную функцию.
|
|
|
|
2 |
|
|
|
|
o |
o |
|
2 |
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
M |
(t T) (t) |
M |
(t T) (t) m (t T) m (t) |
|
|
|||||||||
|
|
o |
o |
|
|
2 |
|
mξ (t T) mξ (t) |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
M |
ξ(t T) ξ(t) |
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как видно, из этого равенства и определения непрерывности, следует непрерывность центрированного случайного процесса и непрерывность математического ожидания.
Положим, ξ(t) - непрерывный случайный процесс и рассмотрим разность
|
|
|
|
o |
|
o |
o |
o |
B0 (T t1,T t2) B0 (t1,t2) M( (T t1) (T t2) (t1) (t2)) |
||||||||
o |
o |
|
o |
o |
o |
o |
o |
o |
M( (T t1) (T t2) (t1) (T t2) (t1) (T t2) (t1) (t2)) |
||||||||
|
o |
o |
o |
|
o |
o |
o |
|
M((( (T t1) (t1)) (T t2)) M( (t1) (T t2) (t2)). |
|
|||||||
Но
o |
o |
o |
|
|
o |
o |
|
2 |
|
|
o |
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
, |
||||||
M((ξ(T t1) ξ(t1))ξ(T t2)) |
M |
|
ξ(T t1) ξ(t1) |
|
|
M |
|
ξ(T t2) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
o |
|
o |
|
o |
|
)) |
|
|
o |
|
) |
|
|
|
|
|
|
|
|||||||
M(ξ(t |
1 |
)(ξ(T t |
2 |
) ξ(t |
2 |
M |
|
ξ(t |
2 |
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
o |
|
o |
|
) |
|
|
|
|
|
|||||
|
M |
|
ξ(T t |
2 |
) ξ(t |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
При уменьшении T в подкоренных выражениях значения корней стремятся к нулю. То есть из непрерывности случайного процесса в точке следует непрерывность ковариационной функции B0ξ (t1,t2).
Верно и обратное утверждение: из непрерывности ковариационной функции следует непрерывность случайного процесса ξ(t).
20
Дифференцирование случайного процесса. Случайный процесс
ξ(t) дифференцируем в точке t в среднеквадратическом смысле, если существует такая случайная функция η(t) - производная в среднеквадратическом процесса ξ(t) в точке t, что
lim M |
|
(t T) (t) |
(t) |
|
2 |
|
dξ(t) |
|
|
|
|
|
|
|
|||||
|
|
0, |
η(t) ξ'(t) |
. |
(1.29) |
||||
|
|
|
|
||||||
T 0 |
|
T |
|
|
|
dt |
|
||
Как видно из этой формулы, для существования производной в точке t требуется непрерывность случайного процесса в точке t. Из дифференцируемости в среднеквадратическом следует дифференцируемость по вероятности
|
|
ξ(t T) ξ(t) |
|
|
|
|
ξ(t T) ξ(t) |
||
lim P |
|
|
ξ (t) |
ε |
0, |
ξ (t) lim |
|
(1.30) |
|
|
T |
|
|||||||
T 0 |
|
|
|
|
|
T 0 |
T |
||
Математическое ожидание случайного процесса |
|
|
равно |
|
|||||||||||||||||||
ξ (t) |
|
|
|||||||||||||||||||||
|
|
|
ξ(t T) ξ(t) |
|
|
|
|
mξ (t T) mξ (t) |
m (t). |
(1.31) |
|||||||||||||
M(ξ (t)) lim M |
|
|
|
|
|
lim |
|
|
|
|
|
|
|||||||||||
|
|
|
T |
T |
|
|
|
|
|||||||||||||||
|
|
T 0 |
|
|
|
|
|
|
T 0 |
|
|
|
|
|
|
ξ |
|
||||||
Если процесс ξ(t) - стационарный, то mξ (t) 0. |
|
|
|
|
|
|
|||||||||||||||||
Корреляционная функция производной: |
|
|
|
|
|
|
B |
(t1,t2 ) |
|
||||||||||||||
|
|
|
|
(t |
1 |
T) (t |
1 |
) (t |
2 |
T) (t |
2 |
) |
|
|
|
|
|||||||
B |
' t1,t2 |
lim M |
|
|
|
|
|
|
|
|
lim |
|
|
T |
, |
||||||||
|
|
T |
|
|
|
|
|
|
T |
|
|
|
|
T2 |
|||||||||
|
|
T 0 |
|
|
|
|
|
|
|
|
|
|
|
|
T 0 |
|
|
|
|||||
где ξT (t) ξ(t T) ξ(t). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для анализа B (t ,t ) вычислим B t ,t и произведем разложе-
ξ 1 2 ξT 1 2
ние её в ряд Тейлора, ограничившись вторыми производными.
BξT t1,t2 M (ξ(t1 T) ξ(t1))(ξ(t2 T) ξ(t2)) M ξ(t1 T)ξ(t2 T)
M(ξ(t1)ξ(t2 T)) M(ξ(t1 T)ξ(t2)) M(ξ(t1)ξ(t2))
Bξ t1 T,t2 T Bξ t1,t2 T Bξ t1 T,t2 Bξ t1,t2
|
|
|
|
|
|
|
|
B |
ξ |
|
B |
|
|
|
T |
2 |
|
|
2B |
ξ |
|
|
2B |
ξ |
|
2B |
|
|
|
||||||
B |
|
(t |
|
,t |
|
) T |
|
|
|
|
|
|
ξ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
ξ |
|
|||||||
ξ |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
t |
|
|
t |
|
|
|
|
|
|
2 |
|
t |
|
t |
|
|
2 |
|
|||||||||||||||||
|
|
|
|
1 |
|
2 |
2 |
|
t |
|
|
1 |
2 |
|
t |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|||||||||
21
B |
|
|
(t |
|
|
,t |
|
|
) T |
|
B |
ξ |
|
|
T |
2 |
|
|
2B |
ξ |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ξ |
1 |
2 |
|
t |
2 |
|
2 |
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
B |
|
|
(t |
|
|
,t |
|
|
) T |
B |
ξ |
|
T |
2 |
|
|
|
2 B |
ξ |
B |
|
(t |
|
,t |
|
) o(T |
3 |
) |
|||||||||||||
ξ |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
ξ |
1 |
2 |
|||||||||||||||||||||||||
|
t |
1 |
|
|
2 |
|
|
|
|
t |
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Из этих выражений получим
|
|
2B |
ξ |
t |
1 |
,t |
2 |
|
|
|
Bξ (t1,t2) |
|
|
|
|
|
. |
(1.32) |
|||
|
|
|
|
|
|
|||||
|
t |
t |
2 |
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
Таким образом, условием дифференцируемости случайного процесса является существование и непрерывность второй смешанной производной случайного процесса. Для стационарного случайного процесса можно получить
|
|
|
|
2B |
ξ |
τ |
|
B |
ξ |
(τ) |
|
|
|
. |
|
|
|
|
|
||||
|
|
|
τ2 |
||||
|
|
|
|
||||
Интегрирование случайного процесса. Положим, случайный процесс
ξ(t) задан в области ξ. Разобьем эту область на интервалы точками
и рассмотрим сумму
n
k 1g(vk ,t) ξ(vk ) (vk vk 1),
где g(vk ,t) - некоторая известная весовая функция. В частности,
можно потребовать g(vk ,t) g(t) и |
ξ |
g(t) dt 1. |
Положим также, что существует некоторый случайный процесс η(t). Случайный процесс ξ(t) будет интегрируемым в среднеквадратическом смысле, если существует случайный процесс η(t) такой, что
|
|
|
|
n |
|
|
|
|
|||
l.i.m. |
|
|
g(vk ,t) ξ(vk ) (vk vk 1) η(t) |
|
|
M |
|
|
|||
max(vk vk 1) |
|
|
|
k 1 |
|
|
|
|
|
0.
(l.i.m. – limit in the mean – предел в среднем)
Случайный процесс η(t) будет называться интегралом от случайного процесса ξ(t) с весовой функцией g(v,t) и обозначаться как
22
