
Случайный процесс
.pdf
Ввиду того, что процессы Ac(t) и As(t) - стационарные и рассматриваются одномерные плотности распределения вероятности, в дальнейшем обозначим x(t) x, φ(t) φ.
Согласно правилам преобразования координат выразим совместную плотность огибающей и фазы как
wA, (x,φ) wAc,As (f1,f2) J ,
где якобиан преобразования равен J x. После соответствующих подстановок получим
|
|
|
x |
|
|
|
|
1 |
|
x |
|
|
|
|
2 |
x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
w |
A, |
(x,φ) |
2 |
exp |
|
|
|
2 |
c |
cosφ m |
c |
|
s |
sinφ m |
s |
|
. |
|||||
|
|
2πσ |
|
|
2σ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Произведем упрощение показателя экспоненты при помощи подстановок
mc mcosβ, |
ms msinβ, |
mc2 ms2 m2, tgβ ms .
mc
В результате получим совместную плотность вероятности
|
|
|
x |
|
|
|
|
1 |
|
x |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. (2.36) |
|
w |
A, |
(x,φ) |
2 |
exp |
|
|
|
2 |
|
2xmcos(φ β) m |
|
|
|||
|
|
2πσ |
|
|
2σ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проинтегрировав по φ, получим одномерную плотность распределения вероятности огибающей узкополосного процесса
|
|
|
|
|
x |
e |
x2 m2 |
|
|
1 |
|
π |
|
x mcos(φ β) |
|
|
||||||||||
|
|
|
|
2σ2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
wA(x) |
|
|
|
|
|
e |
σ2 |
dφ |
= |
|||||||||||||||||
|
σ2 |
|
2π |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
x2 m2 |
|
|
|
|
π |
|
|
|
|
|||||||
|
|
|
|
x |
|
|
|
xm |
|
|
|
|
||||||||||||||
|
|
|
|
|
2σ |
2 |
|
|
|
|
x 0, |
|
(2.37) |
|||||||||||||
|
|
|
|
|
|
e |
|
|
|
I |
0 |
|
|
|
, |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
σ2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
π |
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где I0 |
(z) |
|
|
|
|
ezcos(φ β)dφ |
|
- модифицированная функция Бес- |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
π
селя первого рода нулевого порядка [8].
Плотность распределения вероятности вида (2.37) называется плотностью распределения Райса.
53

Используя совместную плотность распределения вероятности огибающей и фазы wA, (x,φ), проинтегрировав её по x в интервале
(0, ), где величина сos θ φ 0 (для того, чтобы интеграл сходился), получим плотность распределения вероятности фазы
|
|
1 |
|
e |
m2 |
|
|
w (φ) |
|
|
2σ2 |
|
|||
|
|
|
|
||||
|
|
|
|
|
|||
2 |
|
2π |
|
|
|||
|
|
|
|
|
|
m2 сos2(θ φ) |
||
|
|
|
|
|
mсos(β φ) |
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
2σ2 |
||||
|
|
|
e |
|||||
π |
|
|||||||
|
|
|
σ |
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
mCos(β φ) |
||||||
1 Erf |
|
|
|
|
, (2.38) |
||
|
|
|
|||||
|
|
2σ |
|
|
|||
|
|
|
|||||
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
z |
|
|
где Erf z |
|
e t2 |
dt. |
||
|
|
|
|||
π |
|||||
|
0 |
|
|||
Если составляющие Ac(t) и As(t) имеют математические ожидания, равные нулю, mc ms 0 , то плотность распределения вероятности огибающей будет равна
|
x |
|
x2 |
|
|||
|
2σ2 |
|
|
||||
wA(x) |
|
|
e |
, |
(2.39) |
||
σ |
2 |
||||||
|
|
|
|
|
|||
которая называется распределением Релея.
Фаза в этом случае распределена равномерно в интервале π,π . Математическое ожидание и дисперсия распределения Релея рав-
ны соответственно
M A σ |
π |
D A σ2 |
|
|
π |
||
|
, |
|
2 |
|
. |
||
|
2 |
||||||
2 |
|
|
|
|
|
||
2.7 Марковские процессы
Наиболее общей характеристикой случайного процесса является многомерная функция распределения
P(x(t1) x1, x(t2) x2, ,x(tk ) xk )
P(x(t1) x1) P(x(t2) x2 / x(t1) x1), (2.40),P(x(tk ) xk / x(tk 1) xk 1, ,x(t1) x1)
54
Wξ (x1,t1)Wξ (x2,t2 / x1,t1), ,
,Wξ (xi,ti / xi 1,ti 1, ,x1,t1), ,Wξ (xk ,tk / xk 1,tk 1, ,x1,t1).
Как видно, функция распределения в произвольный момент времени ti зависит от значений случайного процесса во все предыдущие моменты времени. Однако на практике существуют процессы, у которых значения процесса в какой-то момент времени ti зависят только от предшествующего момента ti 1. Такие процессы изучались Марковым А.А. и в его честь были названы марковскими. Многомерная функция распределения вероятности марковского процесса имеет вид
k
wξ (x1,x2, xk ,,t1,t2, ,tk ) wξ (x1,t1) wξ (xi,ti / xi 1,ti 1). (2.41)
i 2
Из формулы (2.41) видно для описания марковского процесса достаточно знать одномерную и условные функции распределения вероятности.
В зависимости от состояния пространства значений и времени марковские процессы подразделяются на четыре вида [1], [9] по комбинациям пространства значений (непрерывное, дискретное) случайного процесса и времени (непрерывное, дискретное).
- непрерывный марковский процесс – пространство значений - непрерывно, время – непрерывно. Описывается при помощи функции (2.41) и плотности распределения вероятности (2.42)
k
wξ (x1,x2, ,xk , t1,t2, ,tk ) wξ (x1,t1) wξ (xi,ti / xi 1,ti 1), (2.42)
i 2
- марковская последовательность – пространство значений - непрерывно, время – дискретно. Описывается при помощи функции и плотности распределения вероятности (2.42), но моменты времени
t1,t2 , ,tk принадлежат дискретному множеству,
-дискретный марковский процесс - пространство значений - дискретно, время – непрерывно. Описывается при помощи функции распределения вероятности и условными вероятностями перехода из одного состояния в другое
P(ξ(t1) x1,ξ(t2) x2, ,ξ(tm ) xm )
m |
|
P(ξ(t1) x1) P(ξ(ti) xi /P(ξ(ti 1) xi 1), |
(2.43) |
i 1 |
|
55
где x1,x2,, ,xm - произвольные дискретные значения, принимаемые случайным процессом из некоторого дискретного множества
Xв моменты времени t1,t2, ,tm.
-цепь Маркова - пространство значений - дискретно, время – дис-
кретно. Описывается при помощи функции распределения вероятности и условными вероятностями перехода из одного состояния в другое в дискретные моменты времени
P(ξ(t1) x1,ξ(t2) x2, ,ξ(tk ) xk )
k
P(ξ(t1) x1) P(ξ(ti) xi /P(ξ(ti 1) xi 1),
i 2 |
|
k |
|
P(ξ(t1) x1) P(ξ(ti) xi /P(ξ(ti 1) xi 1), |
(2.44) |
i 2
где {x1,x2, ,xi 1,xi, ,xk} - произвольные дискретные значения, принимаемые случайным процессом из некоторого дискретного множества в дискретные моменты времени {t1,t2, ,ti 1,ti, ,tk}.
Одним из примеров марковских процессов является блуждание точки, отображающий некоторый физический процесс, между границами, которые могут быть как поглощающими, так и отражающими.
2.7.1 Непрерывный марковский процесс
Запишем формулу (2.42) в виде
wξ (x1,x2, ,xk , t1,t2, ,tk ) |
(2.45) |
wξ(x1,t1)wξ (x2,t2 / x1,t1)wξ (x3,t3 / x2,t2) wξ(xk,tk / xk 1,tk 1) |
|
Условные плотности вероятности wξ (xi,ti /xi 1,ti 1) |
называют |
плотностью вероятности перехода из состояния xi 1 в состояние xi за интервал времени (ti 1,ti ). Из (2.45) следует, что двумерная плотность распределения wξ (xi 1,xi,ti 1,ti) в соответствующие момен-
ты времени полностью описывают марковский процесс.
Исходя из общих свойств плотности распределения вероятности, отметим:
|
|
wξ (xi,ti / xi 1,ti 1) 0, |
wξ (xi,ti / xi 1,ti 1) dxi 1, |
|
|
56

tk |
tj |
ti |
|
|
xk |
xj |
xi |
lim wξ (xi,ti /xi 1 |
,ti 1) δ(xi xi 1) |
|
Рис. 2.5 |
|
ti ti 1 |
|
|
|
. |
|
Рассмотрим три момента времени tk tj ti, (Рис.2.5), и соответст-
вующие им состояния xk ,xj,xi. Условная плотность распределения вероятности перехода процесса из состояния xk в состояние xi оп-
ределяется обобщенным уравнением Маркова
wξ (xi,ti / xk ,tk ) wξ (xi,ti /xj,tj) wξ (xj,tj /xk ,tk )dxj, (2.46)
В литературе можно встретить название уравнение (2.46) – уравнение Смолуховского, уравнение Колмогорова-Чепмена.
Если условная плотность вероятности wξ(xi,ti /xk,tk ) зависит от разности моментов времени ti tk τ, то есть,
wξ (xi,ti /xk,tk ) wξ (xi,τ/xk ),
то такой процесс называется однородным во времени (стационарным) марковским процессом.
Колмогоровым А.Н. было получено дифференциальное уравнение, позволяющее найти условную плотность распределения вероятности при определённых допущениях.
2.7.2. Уравнения Колмогорова-Фоккера-Планка
Ввиду того, что в дальнейшем необходимо будет переходить к  пределам, обозначим
пределам, обозначим
t- t |
t |
T |
tk t t, t j t, ti T, |
x |
z |
y |
ξ(t t) x, ξ(t) z, ξ(T) y, |
|
Рис. 2.6 |
|
(Рис. 2.6), [1], [10]. |
|
|
Обобщенные уравнения Маркова в |
|
|
|
|
|
|
|
|
этих обозначениях примет вид |
wξ (y,T/ x,t t) wξ (y,T/z,t) wξ (z,t /x,t t) dz
Предполагаем, что рассматриваемый процесс ξ(t) непрерывный, т.е. с малой вероятностью процесс ξ(t) может получить заметные
57

приращения за малый промежуток времени. Непрерывность марковского процесса понимается в усиленном виде:
lim |
1 |
P( |
|
ξ(t) ξ(t t) |
|
δ/ξ(t t) x) |
|
w(z,t/x,t t)dz 0 (2.47) |
||
|
|
|||||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
||
0 |
t |
|
||||||||
t |
|
|
||||||||
z x δ
для любого постоянного δ 0.
Сделаем предположения - для любого постоянного δ 0 существуют пределы
|
|
|
|
|
|
|
|
|
lim |
1 |
|
|
|
(z x)w(z,t/x,t t)dz a(x,t) |
(2.48) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
t 0 t |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
z x |
δ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
lim |
|
|
|
|
(z x)2 w(z,t /x,t t)dz b(x,t) |
(2.49) |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
t 0 t |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z x |
δ |
|
|
|
|
|
|||
|
Используя свойство функции распределения, запишем |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wξ (y,T/ x,t t) wξ (y,T/ x,t t) wξ (z,t /x,t t)dz. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учтем условие (2.47) и рассмотрим отношение |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
wξ (y,T/x,t t) wξ (y,T/x,t) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
wξ (y,T/ z,t) wξ (z,t / x,t t)dz |
|
|
|
|
|
||||||||||||||
|
t |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
wξ (y,T / x,t) wξ (z,t / x,t t)dz |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
(wξ(y,T/z,t) wξ (y,T/x,t)) wξ (z,t/x,t t)dz |
|
|
||||||||||||||||
|
|
t |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
wξ (y,T/z,t) wξ (y,T/ x,t) wξ (z,t /x,t t)dz |
|
|
|||||||||||||||
|
|
t |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
z x |
δ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
wξ (y,T/z,t) wξ (y,T/x,t) wξ (z,t/x,t t)dz. |
(2.50) |
|
|||||||||||||
|
|
t |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
z x δ
58

Разложим функцию wξ (y,T/z,t) в ряд Тейлора в точке z x и
ограничимся первыми тремя членами разложения:
|
|
|
|
|
1 |
|
kwξ (y,T / z,t) |
|
|
|
wξ (y,T / z,t) wξ (y,T / z,t) |
|
|
|
z x k |
|
|||||
z x |
k! |
zk |
||||||||
|
|
|
|
|||||||
|
|
|
k 1 |
|
|
|
|
|
z x |
|
|
|
|
|
|
|
|
|
|||
wξ (y,T / x,t) z x wξ (y,T/ x,t)
x
z x 2 |
1 |
|
2wξ (y,T/ x,t) |
o z-x 2 . |
|
x2 |
|||
2! |
|
|||
После подстановки разложения функции wξ (y,T/z,t) в (2.50) имеем
|
|
wξ (y,T/x,t t) wξ (y,T/x,t) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
wξ(y,T/z,t) wξ (y,T/x,t) wξ(z,t/x,t t)dz |
|||||||||||||||||
|
t |
|
|||||||||||||||||||
|
|
|
|
|
|
|
z x |
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wξ(y,T/x,t) |
|
1 |
|
|
|
|
z x wξ (z,t/x,t t)dz |
||||||||||||
|
|
|
x |
|
t |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2wξ (y,T/x,t) |
|
|
|
|
|
z x |
δ |
|
|
|
|||||||
|
1 |
|
1 |
|
|
|
z x 2 |
ο(z - x)2 |
wξ(z,t/x,t t)dz. (2.51) |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
x2 |
|
|
t |
|
δ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z x |
|
|
|
||
Перейдем к пределу при t 0. Первое слагаемое в последнем выражении в пределе равно нулю вследствие (2.47). Второе слагае-
мое, в силу (2.48), равно a(x,t) w(y,T/x,t), в третьем слагаемом
x
пренебрежем членами второго порядка малости и оно будет равно, в
|
|
1 |
|
2wξ |
(y,T/x,t) |
||||
силу (2.48), |
|
b(x,t) |
|
|
. Из этих вычислений заключаем, |
||||
2 |
|
|
|||||||
|
|
|
|
x2 |
|||||
что предел левой части (2.51) существует, т.е. |
|||||||||
lim |
wξ (y,T/x,t t) wξ (y,T/x,t) |
|
wξ (y,T/x,t) |
. |
|||||
|
|
||||||||
t 0 |
|
|
|
t |
|
|
|
t |
|
Объединяя все полученные результаты, запишем дифференциальное уравнение
|
w |
ξ (y,T/ x,t) |
|
w |
ξ (y,T/ x,t) |
1 |
|
2wξ |
(y,T/ x,t) |
||
|
|
|
a(x,t) |
|
|
|
|
b(x,t) |
|
|
, (2.52) |
|
t |
|
x |
|
|
|
|||||
|
|
|
|
2 |
|
|
x2 |
||||
которое называется первым уравнение Колмогорова.
59
Запишем без доказательства второе уравнение Колмогорова
|
wξ |
(y,T/ x,t) |
|
a(y,T)wξ (y,T/ x,t) |
|
1 2 b(y,t)wξ |
(y,T/ x,t) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(2.53) |
|
|
T |
|
|
|
y |
|
|
y |
2 |
|||||
|
|
|
|
|
|
2 |
|
|
|
||||||
где |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a(y,T) lim |
|
(z y) w(z,T/ y,T t)dz, |
|
|
(2.54) |
||||||||
|
|
t |
|
|
|||||||||||
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|||
|
|
b(y,T) lim |
1 |
|
(z y)2 w(z,T/ y,T t)dz. |
(2.55) |
|||||||||
|
|
t |
|||||||||||||
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|||
Первое уравнение Колмогорова называют уравнением обращенным в прошлое. Переменными будут x и t T, переменные y и T вводятся через начальное условие w(y,T/x,T) δ(y x).
Второе уравнение Колмогорова называют уравнением, обращенным в будущее. В этом случае переменными будут y и T t, а переменные x и t вводятся через начальное условие w(y,t/x,t) δ(y x) [1]. Второе уравнение Колмогорова называют также уравнением Фок-
кера-Планка.
Предполагается, что коэффициенты a(x,t), b(x,t), a(y,T), b(y,T) известны из физической постановки задачи и требуется найти условные плотности распределения. Оба уравнения Колмогорова принадлежат к параболическому типу дифференциальных уравнений.
Коэффициент a(x,t) характеризует среднюю скорость изменения процесса ξ(t), а коэффициент b(x,t) пропорционален скорости изменения дисперсии процесса ξ(t).
Рассмотрим частный случай второго уравнения Колмогорова - коэффициенты a(x,T) и b(x,T) не зависят ни от координаты x, ни от времени T, т.е. a(x,T) a, b(x,T) b. Тогда уравнение (2.53) будет иметь вид
wξ (y,T/ x,t) |
wξ (y,T/ x,t) |
1 |
|
|
2wξ (y,T/ x,t) |
(2.56) |
||
|
a |
|
|
|
b |
|
|
|
|
|
2 |
|
y2 |
||||
T |
y |
|
|
|
||||
60
Решением уравнения (2.56) будет
|
1 |
|
|
(y x a(T t)) |
2 |
|
|
|
|
|
|
|
. (2.57) |
||||
w(y,T/ x,t) |
|
|
еxp |
|
|
|
||
|
|
2πb(T t) |
|
|
2b(T t) |
|
|
|
|
|
|
|
|
|
|
||
Как видно из (2.57) значения координаты x диффузионного процесса ξ(t) подчинены нормальному закону с дисперсией Dξ(t) b(T t) и математическим ожиданием Mξ(t) x a(T t).
Величины a и b называются коэффициентами сноса и диффузии, соответственно. Они показывают изменение положения среднего значения величины x и величину разброса значения x около среднего значения со временем относительно начала отсчета (x,t).
6.7.3 Винеровский процесс
Винеровским процессом η(t) называется случайный процесс на выходе идеального интегратора (Рис. 2.7), когда на его вход подается нормальный белый шум ξ(t) с параметрами
|
|
|
|
Mξ(t) 0, |
Bξ (τ) |
N0 |
δ(τ), |
|
|
|
|
2 |
|||
(t) |
|
(t) |
|
|
|||
|
|
|
t |
|
|
|
|
|
|
|
|
η(t) ξ(τ)dτ. |
|
(2.58) |
|
|
|
|
|
|
|||
Рис. 2.7 0
Ввиду того, что операция интегрирования является линейной операцией, значения процесса η(t) будут распределены по нормальному закону с математическим ожиданием Mη(t) 0 и ковариационной функцией
t1 t2 |
|
N0 |
t1 t2 |
|
||
Bη(t1,t2) M(ξ(τ1)ξ(τ2))dτ1 dτ2 |
|
δ(τ2 |
τ1)dτ1 dτ2 . |
|||
2 |
||||||
0 0 |
|
|
0 |
0 |
|
|
В зависимости от того t1 t2 или t1 t2 будут разные значения ковариационной функции. Объединяя оба возможных значения, запишем
Bη(t1,t2) |
N0 |
min(t1 |
,t2). |
(2.59) |
|
2 |
|||||
|
|
|
|
61
Как видно из (2.59), значение ковариационной функции зависит от значений моментов отсчета.
Определим дисперсию случайного процесса η(t) в момент времени ti как
2 |
|
|
|
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
ση(ti) Dη(ti) lim Bη |
(ti,t j) |
|
|
ti, |
(i, j 1, 2, i j) |
|
|
|
||||||||||||||||||
2 |
|
|
|
|
||||||||||||||||||||||
|
tj ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
w |
(y,t) |
|
|
|
|
|
|
|
|
|
|
т.е. дисперсия процесса η(t) за- |
||||||||||||||
|
|
|
|
|
|
|
|
висит от момента отсчета. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
N0t=1 |
|
|
|
Таким |
образом, |
одномерная |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
плотность распределения будет |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
равна |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
N0 |
|
t 5 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
y |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
w (y,t) |
|
|
exp |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N0 t |
|
|
|
N0 t |
|
||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис. 2.8 |
|
|
|
|
|
|
|
|
Для |
сравнения |
|
|
построим |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
плотность |
|
|
распределения |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
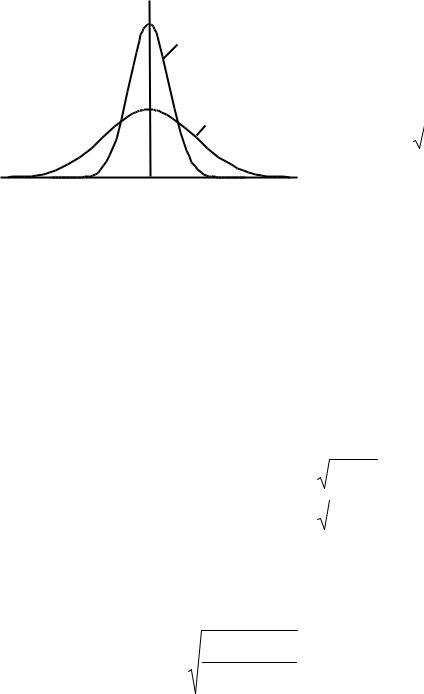
wη(y,t) для N0 t 1 и для |
N0 t 5, считая, что спектральная плот- |
|||||||||||||||||||||||||
ность мощности N0 /2 остается постоянной, а меняется время, Рис. 2.8. Как видно из рисунка, с увеличением времени наблюдения t плотность вероятности становится пологой, т.е. увеличивается разброс значений процесса около математического ожидания.
Запишем двумерную плотность распределения процесса η(t). Для этого вычислим нормированную ковариационную матрицу Rη. Так как Mη(t) 0, то элементы ковариационной матрицы имеют вид
|
|
|
|
|
|
|
|
Bη(ti,tj) |
|
ti |
/tj, |
при ti |
tj |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
R |
η |
(t |
i |
,t |
j |
) |
|
|
|
|
|
|
|
|
|
|
|
, |
(2.60) |
|
ση(ti)ση(tj) |
|
|
|
|
, |
при t |
|
t |
||||||||||
|
|
|
|
|
|
t |
j |
/t |
i |
i |
j |
|
|||||||
где ση2(ti), (i 1, |
|
|
|
|
|
|
|
|
|
|
|||||||||
2) |
- дисперсия случайного процесса η(t) |
в момент |
|||||||||||||||||
времени ti, (i 1, 2) относительно начала отсчета. Формулу (2.60) можно записать в другой форме
Rη(ti,tj)
min(ti,tj)
max(ti,t j)
Ковариационная матрица запишется как
62
