Билет 53

Функции, вычислимые по Тьюрингу.  Пусть  =(₁, ..., _n), n1- произвольный набор целых неотрицательных чисел. Слово 1^1+101^2+10...01^n+1 называется основным машинным кодом или просто кодом набора  в алфавите {0,1} и обозначается k(). Слово 1^+1 также является основным машинным кодом. Для ясности 1³ это 111. Определение. Функция f(x₁,...,x_n), n1, называется частичной числовой функцией, если переменные x_i принимают целые неотрицательные значения из натурального ряда N={0,1,2,…,m,…} и на наборе  функция определена, т.е. f()=f(₁,...,_n), и также принимаeт целые неотрицательные значения. Определение. Частичная числовая функция называется вычислимой по Тьюрингу, если существует МТ Т_f, обладающая следующими свойствами:  1) если функция f() определена, то результатом применения МТ к коду будет являться код целого неотрицательного числа. Т_f(k())=k(f()) 2) если f() не определенна, то либо МТ T_f не применима к слову k(), либо T_f(k()) не является кодом никакого целого неотрицательного числа. Предполагается, что в начальный момент времени головка МТ T_f обозревает самую левую крайнюю единицу слова k(). Если функция f вычислима по Тьюрингу с помощью МТ T_f , то говорят, что МТ вычисляет функцию. Кроме того, т.к. понятие вычислимой функции дано нами через понятие МТ, которое еще математически точно не определено, будем говорить об интуитивно вычисляемой функции. ^ Тезис Тьюринга: Всякий интуитивный алгоритм может быть реализован с помощью МТ. Тезис Черча-Тьюринга: Всякая интуитивно вычисляемая функция вычислима по Тьюрингу. ^ МТ как математическое понятие алгоритма. В каждой МТ имеются: три конечных множества A, Q, T, выделенные элементы a₀A, q₀,q₁Q и программа, представляющая собой отображение вида F: AQ\{q₀}A TQ. (7.3) Определение. МТ называется система вида 0, Q, q0, q1, T, >, где  - программа МТ. Какую бы МТ ни взяли, можно считать, что имеется алгоритм, исходным объектом, промежуточным и окончательным результатами которого являются слова в алфавите А. Предписанием, задающим этот алгоритм, является программа  - точное математическое понятие отображения. Т.о., с математической точки зрения МТ - это алгоритм переработки слов, заданных в алфавите этой машины. Применительно к МТ можно рассматривать все свойства, рассматриваемые применительно к интуитивному понятию алгоритма. В частности, результативность алгоритма и его конечность - это остановится ли МТ за конечное число тактов работы и в какое слово перерабатывается исходное. Чтобы доказать, что функция вычислима по Тьюрингу, необходимо построить МТ, вычисляющую данную функцию. Пример: 1) Построить МТ, вычисляющую функцию f(x,y)=x+y. В качестве внешнего алфавита возьмем  A={a0, 1} , где a0- пустой символ. Тогда в этом алфавите 0 - 1 1 - 11  2 – 111

3 - 1111, и т.д. Q={q0,q1,q2,q3,q4} X и Y будут записаны на ленте и разделены одной ячейкой, содержащей пустой символ. МТ обозревает самую левую крайнюю непустую ячейку. Программа, вычисляющая данную функцию будет иметь вид:  1q11Пq1

a0 q11Пq2 1q21Пq2 a0q2 a0Лq3 1q3 a0Лq4 1q4 a0Лq0  Можно показать, что все арифметические функции вычислимы по Тьюрингу.

БИЛЕТ 38

Логика высказываний.

Логика высказываний — это определённая совокупность формул, т.е. сложных высказываний, записанных на специально сконструированном искусственном языке. Язык логики высказываний включает:

1. неограниченное множество переменных: А, В, С, …, А1 , В1 , С1 , …, представляющих высказывания;

2. особые символы для логических связок: & — «и», v — «или», V — «либо, либо», ? — «если, то», ? — «если и только если», ~ — «неверно, что»»

3. скобки, играющие роль знаков препинания обычного языка. Чтобы использовать меньшее количество скобок, условимся, что операция отрицания выполняется первой, затем идут конъюнкция и дизъюнкция, и только после этого импликация и эквивалентность.

Формулам логики высказываний, образованным из переменных и связок, в естественном языке соответствуют предложения. К примеру, если А есть высказывание «Сейчас день», В — высказывание «Сейчас светло» и С — высказывание «Сейчас холодно», то формула:

А ? В v С , или со всеми скобками: (А ? (В v С)) ,

представляет высказывание «Если сейчас день, то сейчас светло или холодно». Формула:

В & С ? А , или ((В & С) ? А) ,

представляет высказывание «Если сейчас светло и холодно, то сейчас день». Формула:

~ В ? ~ А , или ((~ В) ? (~ А)) ,

представляет высказывание «Если неверно, что сейчас светло, то неверно, что сейчас день» и т.п. Подставляя вместо переменных другие конкретные (истинные или ложные) высказывания, получим другие переводы указанных формул на обычный язык.

Формула, которой не соответствует осмысленное предложение, построена неправильно.

Таковы, в частности, формулы:

(А ?), ( & В), (A v ВС), ( ~ & ) и т.п.

Каждой формуле логики высказываний соответствует таблица истинности, показывающая, при каких подстановках конкретных высказываний в данную формулу она даёт истинное сложное высказывание, а при каких ложное. Например, формула (~ В ? ~ А) даст ложное высказывание, только если вместо В подставить ложное высказывание, а вместо А — истинное.

Всегда истинная формула логики высказываний, или тавтология, — это формула, дающая истинное высказывание при любых подстановках, в неё конкретных (т.е. истинных или ложных) высказываний.

Иными словами, внутренняя структура тавтологии гарантирует, что она всегда превратится в истинное высказывание, какими бы конкретными высказываниями мы ни заменяли входящие в неё переменные.

Всегда ложная формула, или логическое противоречие, всегда превращается влажное высказывание при подстановке конкретных высказываний вместо её переменных.

БИЛЕТ 42

Графы. Основные определения.

Графом называется совокупность двух множеств: вершин и ребер , между элементами которых определено отношение инцидентности – каждое ребро инцидентно ровно двум вершинам , которые оно соединяет. При этом вершина и ребро называются инцидентными друг другу, а вершины 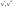, являющиеся для ребра концевыми точками, называются смежными. Именно отношение инцидентности является самым важным элементом графа, т. к. определяет способ объединения множеств и в единый графический объект.

Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой; в этом случае оно называется направленным, или ориентированным, или дугой, и изображается стрелкой, направленной от одной вершины (начала) к другой (концу). Граф, содержащий дуги, называется ориентированным, или орграфом. Граф, содержащий только ребра, называется неориентированным, или н-графом.

Ребра, инцидентные одной и той же паре вершин, называются кратными. Граф, содержащий кратные ребра, называется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей.

Вершина, не инцидентная ни одному ребру, называется изолированной. Граф может состоять только из изолированных вершин. В этом случае он называется нуль-графом.

Граф без петель и кратных ребер называется полным, если каждая пара вершин соединена ребром.

Дополнением графа называется граф , имеющий те же вершины, что и граф , и содержащий только те ребра, которые нужно добавить к графу , чтобы получить полный граф.

Каждому неориентированному графу соответствует ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя дугами, инцидентными тем же вершинам и имеющим противоположные направления.

Локальной степенью (или просто степенью) вершины н-графа называется количество ребер , инцидентных вершине . В н-графе сумма степеней всех вершин равна удвоенному числу ребер графа, т. е. четна, если считать, что петля дает вклад 2 в степень вершины:

.

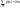Сумма степеней вершин любого графа равна удвоенному числу его ребер. Отсюда следует, что в н-графе число вершин нечетной степени четно.