БИЛЕТ 1
Элементы и множества.
Под множеством интуитивно понимают совокупность определенных, вполне различимых объектов, рассматриваемых как единое целое.
Отдельные объекты, из которых состоит множество, называются элементами множества.
Из определения следует, что элементы множества должны быть:
· вполне различимыми;
· иметь общее свойство.
Будем обозначать множества большими буквами латинского алфавита, а элементы – малыми буквами с индексами или без.
Отношение принадлежности элемента a множеству A обозначается а ϵ А.
Множество B называется подмножеством множества A, если всякий элемент B принадлежит A. Такое отношение обозначается как
В с А. Если В с А и В ≠ А, то В с А. В этом случае говорят, что B есть собственное подмножество A.
Ø - пустое множество;
U – универсальное множество.
Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным. Число элементов в конечном множестве A называется его мощностью и обозначается |A|.
Множества, равномощные множеству натуральных чисел N, называются счетными.
Множества, равномощные множеству вещественных чисел R, называются континуальными.
Если все рассматриваемые в ходе данного рассуждения множества являются подмножествами некоторого множества U , то такое множество называется универсальным.
Основоположником теории множеств Г. Кантором были сформулированы несколько интуитивных принципов, играющих роль аксиом. Нас интересуют два таких принципа.
Принцип объемности. Множества A и B считаются равными (A=B), если они состоят из одних и тех же элементов.
Принцип абстракции. Любая форма P(x) определяет некоторое множество A, а именно множество тех и только тех элементов a ϵ A, для которых P(a), – истинное предложение.
БИЛЕТ 2
Способы задания множеств
-
Перечислительный
А1={3,6,9,…}
-
С помощью характеристического предиката (высказывания)
M = {x : P(x)}
M = {x | P(X)}
A2 = {x : x2-6x+5=0}
A3 = {(x,y) : x,y-вещественные, x2+y2≤1}
-
Порождающие процедуры
-
1 ϵ А4
-
Если х ϵ А4, то 2*х ϵ А4
А4={1,2,4,8,16,…}
-
Решающие процедуры
Ответ: да/нет.
-
Использование характеристического вектора
U={a1,a2,a3,…an}
XA={X1,X2,X3,…XN}
БИЛЕТ 3
Сравнее множеств.
А – подмножество множества В, если каждый элемент множества А является элементом множества В.
А с В, А=В. А с В, В с А.
А с В, елси А с В, А ≠ В.
А с В, если А not c B.
Ø с А.
А с U. (универсальное множество)
Если А с В и В с С, то А с С.
Если множество А – конечное, то |A| - мощность (количество элементов). А и В имеют одинаковую мощность, если существует взаимно-однозначное соответствие.
Множество называется бесконечным, если оно имеет одинаковую мощность с множеством натуральных чисел.
Вещественное множество не является счетным.
БИЛЕТ 4
Операции над множествами.
-
Объединение С=А
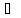 В
В
С = {x | x ϵ A OR x ϵ B}
![]()
-
Пересечение С=А
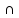 В
В
С = {x | x ϵ A AND x ϵ B}
![]()
-
Разность С = А \ В
C = {x | x ϵ A AND x ∉ B}
![]()
-
Симметрическая разность С= А
 В
В
C = {x | (x ϵ А AND x ∉ B) OR (x ϵ B AND x ∉ A)}
![]()
-
Дополнение С = Ᾱ
Ᾱ = U \ A.
![]()
БИЛЕТ 5
Диаграммы Венна.
Диаграммы Венна – геометрические представления множеств. Построение диаграмм заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов или других замкнутых фигур, представляющих множества.
Точки внутри фигур обозначают элементы множества.
БИЛЕТ 6
Булеан
Множество всех подмножеств множества А называется булеаном и обзначается 2А.
2А={Х|Х с А}
Теорема. Для конечного множества А |2A|= 2|A|.
Доказательство.
Индукция по А. Если |A|=0, то А = Ø и 2ᴓ=Ø => |2ᴓ|=|{ᴓ}=1=20=2|ᴓ|.
Индукционный
переход: Пусть V
A
|A|<k
=> |2A|=2|A|.
Рассмотрим А={a1,a2,…,ak}, |A|=k. Положим: А1={Х с 2А | ak ϵ X} и А2={Х с 2А | ak ϵ X}
БИЛЕТ 7
Свойства операций над множествами
-
Коммутативность
A
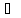 B = B
B = B
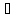 A
A
A
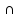 B = B
B = B
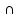 A
A
-
Ассоциативность
(A
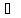 B)
B)
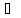 C = A
C = A
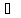 (B
(B
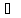 C)
C)
(A
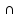 B)
B)
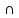 C = A
C = A
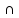 (B
(B
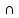 C)
C)
-
Дистрибутивность
(A
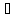 B)
B)
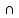 C = (A
C = (A
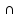 С)
С)
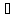 (C
(C
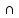 B)
B)
(A
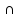 B)
B)
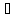 C = (A
C = (A
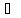 С)
С)
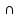 (C
(C
 B)
B)
-
A
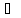 Ᾱ = U
Ᾱ = U -
A
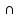 Ᾱ = Ø
Ᾱ = Ø -
Законы нуля и единицы
A
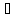 Ø = A
Ø = A
A
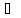 U = U
U = U
A
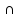 Ø = Ø
Ø = Ø
A
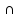 U
= A
U
= A
-
Законы Де-Моргана
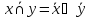
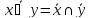
БИЛЕТ 8
Пусть M1 и M2 – два множества. Прямым (декартовым) произведением двух множеств (M1 и M2 ) называется множество всех упорядоченных пар, в котором первый элемент каждой пары принадлежит M1, а второй принадлежит M2 :
M1 х M2 ={(a,b) | a ϵ M1,b ϵ M2}.
БИЛЕТ 9
Между элементами множеств могут устанавливаться различные взаимосвязи, обычно называемые отношениями.
Имеем А1, А2,…,Аn. Рассматриваем их декартовое произведение А1 х А2 х … х Аn.
А
= {(a1, …,an) : a1
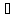 A1, …, an
A1, …, an
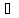 An}.
An}.
n-местные отношения – есть R с A1x A2 x … x An.
Пример трехместных отношений: (a,b,c),c=a+b
Пример.
(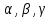 )
)
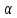 -
человек;
-
человек;
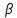 – отец
(
– отец
(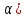
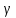 -
мать (
-
мать (
Выражаем через бинарные отношения (декомпозицией):
A1 x A2 x …x An = (A1 x … x An-1) x An.
БИЛЕТ 10
Бинарные отношения. Основные определения.
Бинарным, или двухместным, отношением R называется подмножество упорядоченных пар (а,b)€R прямого произведения M1 х M2 , т. е. R с M1 х M2 . Говорят, что отношение R задано на M1 х M2 .
Часто все элементы принадлежат одному множеству M , т. е. R с M х M , или R с M2 . Так, на множестве студентов группы могут быть заданы такие бинарные отношения, как «жить в одной комнате общежития», «быть моложе», «быть земляком» и т. д. Тогда говорят, что отношение R задано на множестве M . Наравне с обозначением (а,b) ϵ R, R c M2 в литературе используется обозначение аRb, R c M2 .
В общем случае могут рассматриваться n -местные отношения, например отношения между тройками элементов (тернарные) и т. д.
Пример. Равенство x2 + y2 = z2 задает тернарное отношение на множестве целых чисел. Отношение является множеством, включающим все тройки чисел (x, y, z), удовлетворяющие данному равенству. Пусть R c A х B определено в соответствии с рис., из которого следует, что в отношении R задействованы не все, а лишь некоторые
элементы исходных множеств A и B .
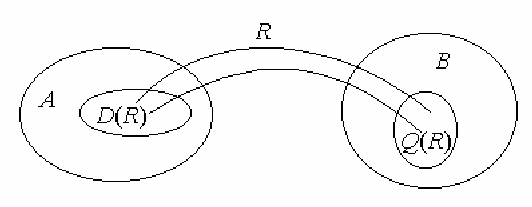
Тогда подмножество D(R) ={a | (a,b) ϵ R} называется областью определения отношения R, а подмножество Q(R) ={b | (a,b) ϵ R} – областью значений этого отношения.
БИЛЕТ 11
Способы задания бинарных отношений
Отношения, определенные на конечных множествах, могут задаваться:
1. Списком (перечислением) пар, для которых это отношение вы- полняется. Например, R ={(a,b), (a,c), (b,d)}.
2. Матрицей – бинарному отношению R c M1 x M2 , где M1 ={a1 ,a2 ,...,an }, M2 ={b1,b2,...,bm }, соответствует матрица размера n х m , в которой элемент cij , стоящий на пересечении i–й строки и j-го столбца, равен 1, если между аi и bj имеет место отношение R , или 0,если нет:
cij=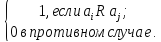
3. Направленным графом, т. е. структурой, состоящей из вершин и дуг (направленных ребер). Элементы множеств отображаются в виде вершин графа, а отношения – в виде дуг, соединяющих эти вершины. Два первых способа одинаково применимы как для отношений, за- данных на разных множествах, так и для отношений на одном множестве. Третий способ больше подходит для отношений на одном множестве, т. к. позволяет получить более компактный граф.
Пример. Пусть M ={1,2,3,4,5,6}. Задать в явном виде (списком), описанием характеристических свойств, матрицей и графом отношение R с M2 , если R означает – «быть строго меньше».
1. С использованием распознающей процедуры можно записать R={(a,b)|a,b ϵ M, a <b}.
2. Списком R ={(1,2),(1,3),(1,4),(1,5),(1,6).(2,3),...}.
3. Матрица данного отношения имет вид
R 1 2 3 4 5 6
1 0 1 1 1 1 1
2 0 0 1 1 1 1
3 0 0 0 1 1 1
4 0 0 0 0 1 1
5 0 0 0 0 0 1
6 0 0 0 0 0 0
Граф имеет вид
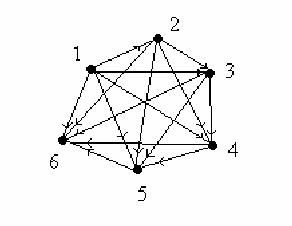
Билет 12
Свойства бинарных отношений
Пусть R – отношение на множестве M , R с M2 , т. е. множество отражается само в себя. Для отношений этого типа могут быть определены следующие свойства:
1. R – рефлексивно, если имеет место aRa для любого a ϵ M . Например, отношение R={(a,b)/a≤b}рефлексивно.
2. R – антирефлексивно, если ни для какого a ϵ M не выполняется aRa. Например, отношение «быть сыном».
3. R – симметрично, если aRb влечет bRa. Например, отношение «жить в одном городе» симметрично.
4. R – антисимметрично, если aRb и bRa влекут a = b, т. е. ни для каких различающихся элементов a и b (a≠b) не выполняется одновременно aRb и bRa. Например, отношение «быть начальником» антисимметрично.
5. R – транзитивно, если aRb и bRc влекут aRc. Например, отношение «быть моложе» транзитивно. Для отношений, заданных на прямом произведении различных множеств, т. е. при R с M1*M2 , свойства рефлексивности, симметричности и транзитивности не определяются.
Пример. Каковы свойства отношения «Быть не больше» (R1 ={(a,b) / a≤b}), заданного на множестве натуральных чисел N?
Рефлексивно, т. к. a ≤ a для всех a ϵ N .
Антисимметрично, поскольку если a≤b и b≤a, то a=b.
Транзитивно, т. к. если a≤b и b≤c, то a≤c.
Пример. Пусть A ={±,⊕,х,*} и пусть R с A х A определено в виде R={(±,±),(±,⊕), (±,*),
(⊕,±), (*,±),(*,*),(х,*),(х,х)}. Каковы свойства отношения?
R не является рефлексивным, т. к. ⊕ ϵ A, но (⊕, ⊕) ∉ R.
R не является симметричным, поскольку (х,*) ϵ R , но (*,х) ∉ R.
R не является антисимметричным, поскольку (⊕, ±) ϵ R и(±,⊕) ϵ R, но ±≠⊕.
R
не является транзитивным, т. к. (⊕,±)
ϵ R и (±,*) ϵ R, но(⊕,*)
 R.
R.
БИЛЕТ 13
Разбиения и отношения эквивалентности.
Отношением эквивалентности (или просто эквивалентностью) называют бинарное отношение на множестве, если оно рефлексивно, симметрично, транзитивно. Например, отношение «жить в одном городе» на множестве людей – эквивалентность.
Отношение эквивалентности имеет важную особенность: эквивалентность R разбивает множество M , на котором оно задано, на непересекающиеся подмножества так, что элементы одного и того же подмножества находятся в отношении R , а между элементами разных подмножеств оно отсутствует. В этом случае говорят, что отношение R задает разбиение на множестве R , или систему классов эквивалентности по отношению R . Мощность этой системы называется индексом разбиения.
БИЛЕТ 14
Оношения порядка.
Оношение порядка – антисимметричное тразитивное отношение.
Отношением нестрогого порядка (или нестрогим порядком) называют бинарное отношение на множестве, если оно рефлексивно, антисимметрично, транзитивно, и отношением строгого порядка (строгим порядком), – если оно антирефлексивно, антисимметрично, транзитивно. Оба эти отношения называются отношениями порядка.
Например, отношение «быть не старше» на множестве людей, «быть не больше» на множестве натуральных чисел – нестрогий порядок. Отношения «быть моложе», «быть прямым потомком» на множестве людей – строгий порядок.
Элементы a,b сравнимы по отношению порядка R на M , если выполняется aRb или bRa .
Множество M , на котором задано отношение порядка R , может быть:
·полностью упорядоченным множеством, если любые два элемента этого множества сравнимы по отношению порядка R;
·частично упорядоченным множеством, если сравнимы лишь некоторые элементы этого множества.
БИЛЕТ 15
Комбинаторные конфигурации. Выборки.
Рассматриваем конфигурации на языке отображения.
Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:
Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
Выборка объема r из элементов – набор элементов ai1, ai2, … air из множества U={a1,a2,…,an}.
Типы выборок: все элементы разны; допускаются одинаковые.
Выборки бывают упорядоченные и неупорядоченные. Упорядоченные выборки называются размещениями, неупорядоченные – сочетаниями. Неупорядоченная – выборка, порядок следования элементов в которой не существенен. Упорядоченная – выборка, порядок следования элементов в которой задан, и и две выборки с разным порядком следования элементов считаются различными.
БИЛЕТ 16
Основные правила комбинаторики.
Основными правилами комбинаторики являются правило суммы и правило произведения.
Правило суммы (∑). Если объект А может быть выбран М способами, а объект В другими N способами, то выбор «либо А, либо В» может быть выполнен M+N способами.
х ϵ А и х ϵ В. Сколько вариантов для выбора элементов х? число=|A|+|B|.
Правило произведения (П). Если объект А может быть выбран М способами и после каждого из таких выборов объект В, в свою очередь, может быть выбран N способами, то выбор «А и В» в указанном порядке может быть выполнен MN способами.
Выбираем х ϵ А и у ϵ В (не зависит, что сперва), А и В могут быть как одинаковыми, так и разными. Число способов=|A|*|B|.
(x,y) ϵ A x B. A x B – декартово произведение. А х В = {(x,y)|x ϵ A, y ϵ B}. Число элементов в декартовом произведении равно: |A x B| = |A|*|B|.
Декартово произведение: А1 х А2 х А3 х … х Аn ={(x1, … , xn) | xi ϵ Ai}.
БИЛЕТ 17
Размещения.
Размещения – упорядоченные независимые выборки.
U(n,r) – число n элементов по r упорядоченных с допустимыми повторениями.
U ϵ A. |A|= n. Перестановки – все элементы разные.
В комбинаторике размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.
В отличие от сочетаний, размещения учитывают порядок следования предметов. Так, например, наборы (2,1,3) и (3,2,1) являются различными, хотя состоят из одних и тех же элементов {1, 2, 3} (то есть совпадают как сочетания).
Количество
размещений из n по k,
обозначаемое ![]() ,
равно убывающему факториалу:
,
равно убывающему факториалу:
![]()
При k=n количество размещений равно количеству перестановок порядка n:
![]()
По правилу
умножения количество размещений с
повторениями из n по k,
обозначаемое ![]() ,
равно:
,
равно:
![]()
БИЛЕТ 18
Сочетания.
Если элементы неупорядоченной выборки попарно различны, то она называется сочетанием без повторений, сочетанием с повторениями, если в выборке элементы могут повторяться.
В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данного множества, содержащего n различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Так, например, наборы (3-элементные сочетания, подмножества, k=3) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n=6) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
В общем случае число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-й диагонали и n-й строки треугольника Паскаля.[1]
Число
сочетаний из n по k равно биномиальному
коэффициенту:
![]()
Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.
Число сочетаний с повторениями из n по k равно биномиальному коэффициенту:
![]()
БИЛЕТ 19
Булевы функции. Способы задания булевых функций.
Логические, переключательные.
Джорж Буль (ввел понятие в 1864г).
B={0,1}.
0 – ложь (false), 1 – истина (true).
f(x1,…,xn) – функции алгебры логики, если аргументы функции и сама функция принимает значение из В.
Способы задания булевых функций.
-
Табличный

Лексографический порядок: меньше -> больше.
-
Векторный способ.
Zf(x1,x2,x3) = (f(0,0,…,0),f(0,0,…,1),…,f(1,1,…,1))
-
Задание областью истинности.
Задаем множество:
Nf={(α1,α2,…,αn) : (α1,α2,…,αn)=1}
Пример. Nf={(011),(101),(110),(111)} или Nf={3,5,6,7}
-
Формулы.
-
И другие.
БИЛЕТ 20
Количество булевых функций от n переменных. Фиктивные и существенные переменные.
Обозначения: P2 – множество всех булевых функций; P2n – множество булевых функций от переменных x1,x2,…,xn.
T1.
P2(n)=|P2n|=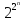
[Каждой
функции P2n
можно поставить в соответствие вектор
β=(β1,β2,…,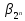 ).
С другой стороны каждому двоичному
вектору 2n
соответствует булева функция
).
С другой стороны каждому двоичному
вектору 2n
соответствует булева функция
N=2n
P2(n)=2N=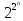 ]
]
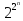 растет
очень быстро:
растет
очень быстро:
P2(1)=4
P2(2)=16
P2(3)=256
Фиктивные и существенные переменные.
Опр. Если задана булева функция f=f(x1,…,xn), то xi , 1≤i≤n, называют фиктивной, если f(x1,…,xi-1,0,xi+1,…, xn)≡ f(x1,…,xi-1,1,xi+1,…, xn).
Если функция не является фиктивной, ее называют существенной.
xi – существенная, если существует (α1,…,αn) :
f(α1,…,αi-1,0,αi+1,…,αn) ≠ f(α1,…,αi-1,1,αi+1,…,αn).
Пример. f(x,y) = cosx+sin2y+cos2y
g(x)=cosx+1. Одно и тоже.
Булевы функции рассматриваем с точностью до фиктивных переменных.
Опр. f=g, если функцию g можно получить из функции f добавлением или изъятием фиктивных переменных.
БИЛЕТ 21
Элементарные булевы функции.
![]()
g1(0)=0
g1(1)=0
g3(x)=x
g4-инверсия, отрицание.
![]()
f1 – конъюнкция, логическое умножение, “И”
f2 – дизъюнкция, логическое сложение, “ИЛИ”
f3 – сложение по модулю 2, исключение или, «либо-либо».
f4 - импликация
f5 - эквивалентность
f6 – штрих Шеффера, «функция не “И”»
f7 – стрелка Вебба, «не “ИЛИ”».
БИЛЕТ 50
Неформализованное понятие алгоритма
Термин пошел от фамилии азиатского ученого Ал-Хорезмы.
Под алгоритмом принято понимать конечную совокупность инструкций (команд), согласно которой работает исполнитель алгоритма.
Для алгоритма характерны следующие свойства:
-
Пошаговость;
-
Дискретность (точность, четкость);
-
Элементарность каждого шага;
-
Детерминированность каждого шага (такт);
-
Направленность;
-
Должны быть четко указаны форматы входных и выходных данных;
-
Начальная (стартовая) команда и команда остановки должны выполняться.
Долгое время это неформальное понятие алгоритма удовлетворяло потребности.
В начале 20в.появилась необходимость уточнения (формализации) данного понятия. Практически одновременно появилось несколько формализаций. Одной из них было понятие «Машины Тьюринга».
БИЛЕТ 22
Булевы формулы. Представление булевых функций формулами. Эквивалентность формул.
*учебник*
{
Формулы, содержащие только операции конъюнкции, дизъюнкции и отрицания называются булевыми.
Следующие две теоремы, приведенные без доказательств, устанавливают правила перехода от одного базиса к другому.
Теорема 1 Всякая логическая формула может быть представлена булевой
формулой.
Теорема 2 Если все функции функционально полной системы ∑* представимы формулами над ∑ , то ∑ также функционально полна. Таким образом, чтобы перейти в записи логической формулы от одного базиса к другому, нужно просто заменить все операции первого базиса через операции второго базиса.
}
*лекции*
Опр. Пусть задано множество А булевых функций A={f1,f2,…}. Введем понятие булевых формул на базисе А.
Определение индуктивности.
-
Функция fi ϵ A является формулой в базисе А.
-
fi(х1,..,хn) ϵ A.
Выражения: F1, F2, …, Fn.
Fj-любой символ переменной, либо формула в базисе А. Тогда выражение fi(F1, …, Fn) – формула в базисе А.
Каждой формуле соответствует булева функция, которая вычисляется по формуле, по обычным правилам суперпозиции.
Базис Буля.
A0={x&y, x˅y, ̚x}
Базис Жегалкина.
А1={x*y,x⊕y, 0, 1}
Опр. Две формулы F и G называются эквивалентными, если им соответствует одна и та же булева функция: F=G.
БИЛЕТ 23.
Основные эквивалентности в алгебре-логики.
1. Ассоциативность:
x * (y * z ) = (x * y) * z
x ˅ (y ˅ z) = (x ˅ y) ˅ z
2. Коммутативность:
х1 * х2 = х2 * х1
х1 ˅ х2 = х2 ˅ х1
3. Дистрибутивность:
x * (y ˅ z) = x * y ˅ x * z .
x ˅ (y * z) = (x ˅ y) * (x ˅ z)
(x⊕y) * z = (x*z) ⊕ (y*z)
4. Идемпотентность:
x * x = x
x ˅ x = x.
5. Закон двойного отрицания:
 =
x .
=
x .
6. Законы нуля и единицы:
х * 1 = х
х * 0 = 0
х ˅ 1 = 1
х ˅ 0 = х
7. Законы де Моргана:
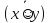 =
=
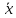 &
&

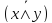 =
=
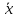 ˅
˅
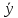
8. Закон противоречия:
А * Ᾱ = 0 .
9. Закон всеобщности:
А ˅ Ᾱ =1.
10. Законы связанные со сложением по модулю 2.
х ⊕ х = 0
х
⊕
1=
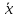
11.Законы позволяющие представить элементарные функции в классическом базисе.
x
⊕
y = (x
*
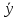 )
˄ (
)
˄ (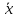 * y)
* y)
x
⊕
y
= (x
˅
y)
* (
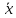 ˅ y)
˅ y)
x
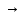 y =
y =
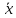 ˅ y
˅ y
x
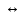 y = (x
y = (x
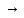 y) & (y
y) & (y
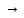 x)
x)
x
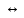 y = (x * y) ˅ (
y = (x * y) ˅ (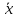 *
*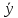 )
)
x
| y = ̚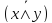
x
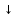 y
=
y
=

12) Законы полезные для упрощения
x ˅ (x * y) = x –закон поглощения
x & (x ˅ y) = x
x ˅ ( ̚ x * y) = x ˅ y
x & y + x & y = x – закон склеивания
Особенность данных эквивалентных соотношений в том, что:
·они не выводимы друг из друга. Убедиться в их справедливости можно путем построения таблиц истинности;
·этих соотношений достаточно для выполнения любых эквивалентных преобразований.
БИЛЕТ 24
Связь между алгеброй множеств и алгеброй логики.
Пусть
имеется система множеств x1,x2,…,xn,и
определены операции над множествами.
Мы можем рассматривать операции x
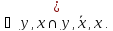 Вместо этих теоретико-множественных
операций мы можем рассматривать
логические операции.
Вместо этих теоретико-множественных
операций мы можем рассматривать
логические операции.
x
v
y,
x
˄
y,
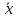 .
.
Составим 2 системы:
S1
= (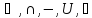 )
- алгебра множеств
)
- алгебра множеств
S2 = (v, ˄, - ,1, 0) - булева алгебра
S1 S2.
S2.
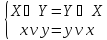
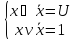
На примере закона Де Моргана.
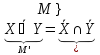 (1)
(1)
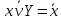 ˄
˄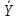 (2)
(2)
![]()
|
|
|
M’ |
M” |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X Y |
|
|
|
0 0 |
|
|
|
0 1 |
|
|
|
1 0 |
|
|
|
1 1 |
|
|
Связь между алгеброй множеств и алгеброй логики заключается в том, что есть 2 изоморфные системы.
БИЛЕТ 41
Основная теорема теории логического вывода.(продолжение билета 40)
(A
-> B) = v B
v B

A
&
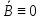 (доказательство от противного).
(доказательство от противного).
БИЛЕТ 25
Понятие двойственности. Принцип двойственности.
Опр.
Для заданной булевой функции
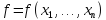 двойственной к ней называют:
двойственной к ней называют:
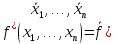 ).
).
Замечания.
-
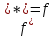
-
F=G
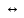 F*=G*
F*=G* -
x*=x
{
(x)*=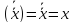
|
x |
f=x |
f* |
|
0 1 |
0 1 |
0 1 |
}
-
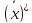 =
=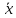
-
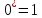
-

-
(x&y)*=x˅y
-
(x˅y)*=x&y
(&,˅,-,0,1)
(˅,&,-,1,0)
Пусть
задана булева функция
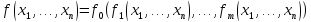 .
.
Замечание. В функциях fi, i=1,…,m некоторые переменные могут быть фиктивными.
Тогда
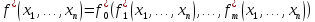
[
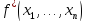 =
=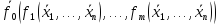 =
=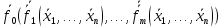 =
=
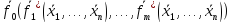 =
=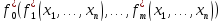
]
Следствие. Если задана булева функция формулой F в базисе Б0=(x&y,x˅y,-,0,1), то для получения двойственной функции достаточно сделать замену:
(&,˅,-,0,1)
(˅,&,-,1,0)
БИЛЕТ 26
Разложение булевых функций по переменным.
Т. о разложении булевой функции по переменным.
Для
любой булевой функции f=f(x1,…,xn)
и V
1≤k≤n
справедливо представление f(x1,…,xn)=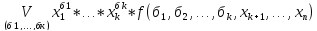 ,
где x1=x,
x0=
̚ x.
,
где x1=x,
x0=
̚ x.
Возьмем произвольный набор Z=(α1,…,αn) и подставим в левую и правую части формулы:
Л.Ч.=f(α1,…,αn)
П.Ч.=
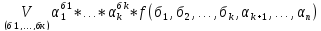 =
=
{
10=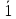 =0;
01=0;
11=1;
00=
=0;
01=0;
11=1;
00=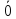 =1;
=1;
 }
}
=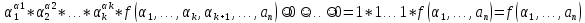
Правая часть совпала с левой.
Следствие1. Формула разложения булевой функции по переменным:
Положим k=1. Возьмем разложение по последней переменной.
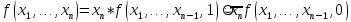
Следствие2. Разложение функции в совершенную дизъюнктивную нормальную формулу (СДНФ).
V
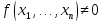 справедливо
справедливо
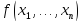 =
=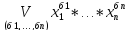 .
.
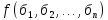 =1.
=1.
Возьмем в теореме случай k=n, т.е. разложение по всем переменным.
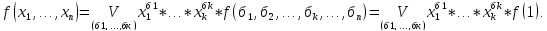
Следствие3. О представимости любой функции в классическом базисе.
Любую булеву функцию можно представить в виде формулы над базисом.
Б0={x&y,x˅y,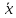 }
}
f≠0 СДНФ
f≡0
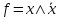
Замечание.
Для любой булевой функции
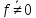 существует представление в виде СДНФ
и это представление является единственной.
существует представление в виде СДНФ
и это представление является единственной.
БИЛЕТ 27
Совершенные дизъюнктивные нормальные формы (СДНФ)[сумма произведений ˅&].
Система операций булевой алгебры полна, и переход от табличного задания любой логической функции к формуле булевой алгебры всегда возможен. Сформулируем очень важный для практики способ перехода от табличного задания логической функции к булевой формуле. Он
включает следующие действия:
·для каждого набора значений переменных x1, x2 ,..., xn , на котором функция f (x1, x2 ,..., xn ) равна 1, выписываются конъюнкции всех переменных;
·над теми переменными, которые на этом наборе равны 0, ставятся отрицания;
·все такие конъюнкции соединяются знаками дизъюнкции.
Полученная таким образом формула называется совершенной дизъюнктивной нормальной формой (СДНФ) логической функции.
Для каждой функции СДНФ единствена.
Таким образом, СДНФ функции f (x1, x2 ,..., xn ) представляет собой дизъюнкцию элементарных конъюнкций: D = K1 ˅ K2 ˅ ... ˅ Km, где все конъюнкции имеют одинаковое число сомножителей, равное числу логических переменных, а число конъюнкций равно числу наборов значений переменных x1, x2 ,..., xn , на которых функция f (x1, x2 ,..., xn) равна 1. Любые другие записи логической функции, вида D = K1 ˅ K2 ˅ ... ˅ Km, не отвечающие этим условиям, называются
дизъюнктивными нормальными формами (ДНФ) этой функции.
БИЛЕТ 28
Совершенные конъюнктивные нормальные формы (СКНФ)[произведение сумм &˅].
Утверждение. Для любой булевой функции f=f(x1,…,xn),f≠1 справедливо представление
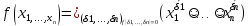
Имеем: f*≠ 0. Теперь построим СДНФ для f*.
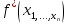 =
=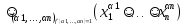
Возьмем двойственную от обеих частей уравнения.
 =
=
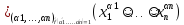 =
=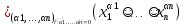 =
=
Делаем
замены:
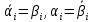 .
.
=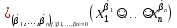 .
.
Замечание.
Для каждой булевой функции
 ≠
1 существует представление в виде СКНФ
и это представление является единственным.
≠
1 существует представление в виде СКНФ
и это представление является единственным.
БИЛЕТ 54
Тезис Тьюринга-Чёрча.
Класс функций, вычислимых алгоритмически (в интуитивном смысле слова), совпадает с классом функций вычислимых по Тьюрингу.
Доводы:
-
Все формализации понятия алгоритма и алгоритмически вычислимой функции оказались равнообъемными.
Примеры формализации: частично рекурсивные функции Чёрча, машины Комогорова-Успенского (мощнее машины Тьюринга), программы на алгоритмическом языке (Pascal).
-
Любая функция по Тьюрингу является алгоритмически вычислимой.
-
Все функции, которые признавались алгоритмически вычислимыми, оказались вычислимыми по Тьюрингу.
-
Деятельность тысяч программистов.
БИЛЕТ 29
Полиномы Жегалкина.
В алгебре логики обычно выделяют 3 кононические формы представления функции в виде формулы:
-
СДНФ
-
СКНФ
-
Полиномы Жегалкина
Моном
– формула вида 0,1,
 .
.
Полином Жегалкина:
P=M1⊕M2⊕…⊕Mk, Mi – моном.
Все мономы попарно различны.
Теорема. Любую булеву функцию можно представить в виде полинома Жегалкина и это представление является единственным.
[
I. Доказываем представимость функции в виде полинома Жегалкина.
Рассмотрим 2 случая
-
f ≡ 0, F=0
-
f ≠ 0, тогда
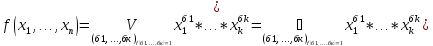 *)
*)
|
x y |
x ˅ y |
x
|
|
0 0 |
0 |
0 |
|
0 1 |
1 |
1 |
|
1 0 |
1 |
1 |
|
1 1 |
1 |
0 |
Можем заменить ˅ на ⊕, т.к. никакие два слагаемых в СДНФ≠1.
K1=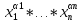 ; K2=
; K2=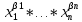
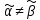
K1*K2 ≡ 0
Значит,
существует j
(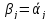 )
)
Сделаем
преобразования
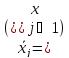
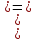
Раскрываем
скобки, приводим подобные по правилу
А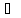 А=0.
А=0.
В
итоге получим полином Жегалкина
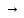 для каждой функции существует полином
Жегалкина.
для каждой функции существует полином
Жегалкина.


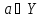
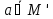
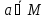
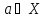
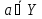
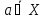
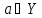
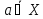
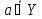
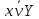
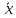 ˄
˄