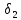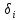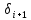II. Доказываем единственность.

Воспользуемся принципом Дирихле.

Подсчитаем количество полиномов Жегалкина.

. То есть 2ⁿ отличных от нуля.

Пустой моном=1.

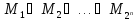
Образуем полином:

Мономов = N=2ⁿ

Полиномов = 2^N=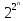

Если ничего не включили, то 0.

|]

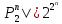БИЛЕТ 30

Понятие функциональной полноты системы булевых функций. Полнота системы {И, ИЛИ, НЕ}.

Определение. Множество функций алгебры логики А называется полной системой (в Р2), если любую функцию алгебры логики можно выразить формулой над А. Теорема. Система А = {v, &, ─} является полной.

Доказательство. Если функция алгебры логики f отлична от тождественного нуля, то f выражается в виде совершенной дизъюнктивной нормальной формы, в которую входят лишь дизъюнкция, конъюнкция и отрицание. Если же f≡ 0, то f = x*(─x). Теорема доказана.

БИЛЕТ 31

Замыкание и замкнутые классы.

1°. Понятие замкнутого класса.

Определение 1. Пусть A ⊆ P2. Тогда замыканием A называется множество всех функций алгебры логики, которые можно выразить формулами над A.

Обозначение: [A].

Имеют место следующие свойства:

1) [A] ⊇ A;

2) A ⊇ B ⇒ [A] ⊇ [B], причём, если в левой части импликации строгое вложение, то из него вовсе не следует строгое вложение в правой части — верно лишь A ⊃ B ⇒ [A] ⊇ [B];

3) [[A]] = [A].

Определение 2. Система функций алгебры логики A называется полной, если [A] = P2.

Определение 3. Пусть A ⊆ P2. Тогда система A называется замкнутым классом, если замыкание A совпадает с самим A: [A] = A.

2°. Примеры замкнутых классов.

Класс T₀ = {f (x₁, …, x_n) | f (0, …, 0) = 0}.

Классу T₀ принадлежат, например, функции 0, x, xy, x ∨ y, x ⊕ y.

Классу T₀ не принадлежат функции 1, x , x → y, x | y, x ↓ y, x ~ y.

Класс T₁ = {f (x₁, …, x_n) | f (1, 1, …, 1) = 1}.

Классу T₁ принадлежат функции 1, x, xy, x ∨ y, x → y, x ~ y.

Классу T₁ не принадлежат функции 0, x , x ⊕ y, x | y, x ↓ y.

Класс L линейных функций.

Определение 4. Функция алгебры логики f (x₁, …, x_n) называется линейной, если

f (x₁, …,x_n) = a₀ ⊕ a₁ x₁ ⊕ … ⊕ a_n x_n, где a_i ∈ {0, 1}.

Иными словами, в полиноме линейной функции нет слагаемых, содержащих конъюнкцию.

Классу L принадлежат функции 0, 1, x = x⊕1, x ~ y, x ⊕ y.

Классу L не принадлежат функции xy, x ∨ y, x → y, x | y, x ↓ y.

Класс S самодвойственных функций.

Определение 2. Функция алгебры логики f (x₁, …, x_n) называется самодвойственной, если f (x₁,…, x_n) = f* (x₁,…,x_n).

Иначе говоря, S = {f | f = f*}.

Определение 2. Функция алгебры логики f (x₁,…,x_n) называется монотонной, если для любых двух сравнимых наборов ~α и ~β выполняется импликация ~α≤ ~ β ⇒f(~α) ≤ f (~ β)

Класс M всех монотонных функций.

Классу M принадлежат функции 0 , 1 , x , xy , x ∨ y, m (x, y, z) = xy ∨ yz ∨ zx.

Классу M не принадлежат функции x , x | y , x ↓ y , x ⊕ y , x ~ y , x → y

БИЛЕТ 40

Логические высказывания и булевы функции.

Под высказыванием (суждением) понимают форму мысли, которая выражает соответствие или несоответствие ее действительности. Высказывание может быть истинным или ложным. Из одних высказываний можно получить другие с помощью логических связок (&, v). Каждому высказывании соответствует булева переменная, каждой логической связке – булева операция.

Высказывания могут быть истинными и ложными. Также есть логические связки.

А => B. Из А логически следует высказывание В, если всякий раз когда А истинно, В тоже истинно.

(А1, …, An) =>B. Логически следует В, если (А1, …, An) – истинно, и В тоже истинно.

A => B  (A -> B) 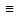1.

(А1, …, An)=> B ((А1 & …& An) -> B)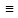1.

БИЛЕТ 36

Универсальные методы синтеза схем из функциональных элементов.

Теорема. Существует метод синтеза схем из функциональных элементов такой, что для любой булевой функции f(x1,…,xn) строится ее реализующая схема S, такая, что

L(S) ≤ 3*2ⁿ + n – 5 , отсюда:

Следствие. L(n) ≤ 3*2ⁿ + n – 5

Замечание.

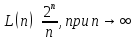
БИЛЕТ 32

Классы Поста.

Критерий Поста — одна из центральных теорем в теории булевых функций, устанавливающая необходимое и достаточное условие для того, чтобы некоторый набор булевых функций обладал достаточной выразительностью, чтобы представить любую булеву функцию. Впервые сформулирован американским математиком Эмилем Постом.

Булева функция — это функция типа , где , а  — арность. Количество различных функций арности  равно , общее же количество различных булевых функций бесконечно. Вместе с тем, очевидно, что многие функции могут быть выражены через другие с использованием оператора суперпозиции. Например, давно известно, что из дизъюнкции и отрицания можно, используя законы де Моргана, получить конъюнкцию. Кроме того, любая булева функция (за исключением тождественного нуля) может быть представлена в виде ДНФ, то есть, в терминах конъюнкции, дизъюнкции и отрицания. Возникает естественный вопрос: как определить, будет ли данный набор функций достаточным, чтобы представить любую булеву функцию? Такие наборы называются функционально полными. Теорема Поста даёт ответ на этот вопрос. Поскольку условие теоремы является необходимыми и достаточным, её называют также критерием.

Идея теоремы состоит в том, чтобы рассматривать множество всех булевых функций  как алгебру относительно операции суперпозиции. Сейчас она носит имя алгебра Поста. Эта алгебра содержит в качестве своих подалгебр множества функций, замкнутых относительно суперпозиции. Их называют ещё замкнутыми классами. Пусть  — некоторое подмножество .Замыканием  множества  называется минимальная подалгебра , содержащая . Иными словами, замыкание состоит из всех функций, которые являются суперпозициями . Очевидно, что  будет функционально полно тогда и только тогда, когда . Таким образом, вопрос, будет ли данный класс функционально полон, сводится к проверке того, совпадает ли его замыкание с .

БИЛЕТ 35

Реализация дешифратора в классе схем из функциональных элементов (схема для выборки элементов).

*учебник*

{

Дешифратором Qn порядка n называется схема из функциональных элементов с n входами x₁, x₂, …, x_n и 2ⁿ выходами z0, z₁,…,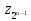 такая, что если |x1x2…xn| = i, то zi = 1 и zj = 0 при i ≠ j.

Заметим, что если i = (i₁, i₂, …, i_n)₂, то z_i(x₁,…,x_n ) = .

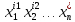Лемма. Существует дешифратор Qn с числом элементов, не превосходящим n2ⁿ⁺¹.

Доказательство. Для реализации каждой z_i достаточно взять ровно n–1 конъюнкций и не более n отрицаний, то есть всего менее, чем 2n функциональных элементов. Всего различных конъюнкций ровно 2ⁿ, и сложность дешифратора не превосходит n²ⁿ⁺¹.

}

*лекции*

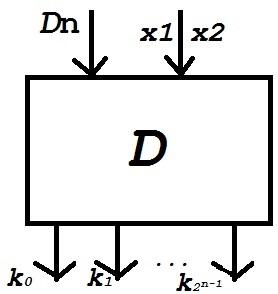
Kj=,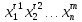

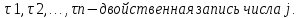
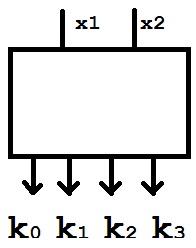
k₀ =

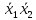
k1 =

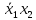
k2 =

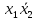
k3 =

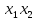
Тривиальные методы основаны на автономной реализации элементарных конъюнкций.

БИЛЕТ 45

Геометрическая реализация графов

*лекции*

{

Пусть 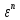– евклидовое n-мерное пространство. Геометрическим графом называют Г=(V,E), где V - множество вершин (точек в этом евклидовом пространстве), Е – множество ребер.

Геометрические графы не должны иметь самопересечений и взаимных пересечений.

Теорема. Любой конечный граф можно представить в виде геометрического графа в трехмерном евклидовом пространстве.

Доказательство.

Пусть G=(V,E) – трехмерный абстрактный граф.

Построим аналог:

V = {V₁,…,V_p}

E = {e₁,…e_q}

Г = (V’,E’) – изоморфность G.

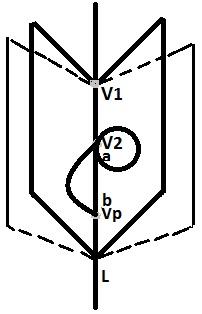
Через прямую L проводим q полуплоскостей (число q конечное). Для каждого ребра e_j выберем свою полуплоскость e_j = (а,b). Если a≠b, то проводим полуокружность. Если а=b, то в этой полуплоскости проводим окружность единичного радиуса, который касается прямой l в точке а. По построению видим, что Г – геометрический граф, потому что каждая линия лежит в своей полуплоскости, т.е. GГ.

}

БИЛЕТ 33

Критерий полноты.

Теорема 12 (теорема Поста). Система функций алгебры логики A = {f1, f2, …} является полной в P2 тогда и только тогда, когда она не содержится целиком ни в одном из следующих классов: T0, T1, S, L, M.

Доказательство. Необходимость. Пусть A — полная система, N — любой из классов T₀, T₁, S, L, M и пусть A ⊆ N. Тогда [A] ⊆ [N] = N ≠ P2 и [A] ≠ P2. Полученное противоречие завершает обоснование необходимости.

Достаточность. Пусть A ⊄ T₀, A ⊄ T₁, A ⊄ M, A ⊄ L, A ⊄ S. Тогда в A существуют функции f₀ ∉ T₀, f₁ ∉ T₁, f_m ∉ M,

f_l ∉ L, f_s ∉ S. Достаточно показать, что [A] ⊇ [f₀, f₁, f_m, f_l, f_s] = P2. Разобьём доказательство на три части: получение отрицания, констант и конъюнкции.

a) Получение ─x . Рассмотрим функцию f₀ (x₁, …, x_n) ∉ T0 и введём функцию φ₀(x) =f₀(x, x, …, x). Так как функция f₀ не сохраняет нуль, φ₀(0) = f (0, 0, …, 0) = 1. Возможны два случая: либо ϕ₀(x) = ─x , либо φ0 (x) ≡ 1. Рассмотрим функцию f₁(x₁, …, x_n) ∉ T₁ и аналогичным образом введём функцию φ₁(x) = f₁(x, x, …, x). Так как функция f₁ не сохраняет единицу, φ₁(1) = f (1, 1, …, 1) = 0. Возможны также два случая: либо ϕ₁( x) = ─x , либо φ1 (x) ≡ 0. Если хотя бы в одном случае получилось искомое отрицание, пункт завершён. Если же в обоих случаях получились константы,

то согласно лемме о немонотонной функции, подставляя в функцию f_m ∉ M вместо всех переменных константы и тождественные функции, можно получить отрицание.

Отрицание получено.

b) Получение констант 0 и 1. Имеем f_s ∉ S. Согласно лемме о несамодвойственной функции, подставляя вместо всех переменных функции f_s отрицание (которое получено в пункте a) и тождественную функцию, можно получить константы: [f_s, x ] ∋ [0, 1]. Константы получены.

c) Получение конъюнкции x · y. Имеем функцию f_l ∉ L. Согласно лемме о нелинейной функции, подставляя в функцию f_l вместо всех переменных константы и отрицания (которые были получены на предыдущих шагах доказательства), можно получить либо конъюнкцию, либо отрицание конъюнкции. Однако на первом этапе отрицание уже получено, следовательно, всегда можно получить конъюнкцию:

[f_l, 0, 1, ─x ] ∋ [xy, ─xy]. Конъюнкция получена.

В результате получено, что [f₀ , f₁ , f_m , f_l, f_s] ⊇ [ ─x,xy] = P₂ . Последнее равенство следует из пункта 2 теоремы 4. В силу леммы 2 достаточность доказана.

БИЛЕТ 34

Реализация булевых функций схемами из функциональных элементов.

*учебник*

{

Одно из основных приложений булевых функций лежит в области создания схем функциональных элементов или функциональных схем, которые можно реализовать в виде электронных устройств с конечным числом входов и выходов, причем на каждом входе и выходе может появляться только два значения. Такие устройства собраны из функциональных элементов, генерирующих основные булевы операции.

Соединяя функциональные элементы вместе, мы получаем функциональную схему. С ее помощью можно реализовать любую булеву функцию.

Сложностью схемы из функциональных элементов называется число функциональных элементов в схеме.

}

*лекции*

Дизъюнктор, инвектор.

СФЭ – схемы из функциональных элементов.

F=(f₁, f₂, …, f_m)

L(S) – сложность – количество функциональных элементов в схеме.

L(S) = minL(S) – наименьшее количество элементов, с помощью которых можно построить схему.

L_A(f) = L(S_A(f)) – сложность схемы.

L_A(n) = maxL_A(f), f ϵ 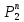. Макс.берется по всем переменным.

Функция Шеннона для А.

L(f) = minL(S)

L(n) = maxL(f)

L_A(n) L(n)

Пусть в СДНФ l (эль) слагаемых.

f = k₁˅k₂˅…˅k_l

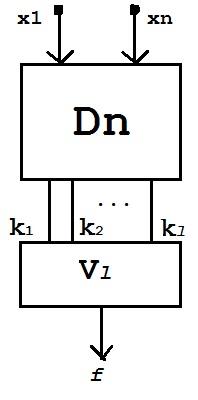
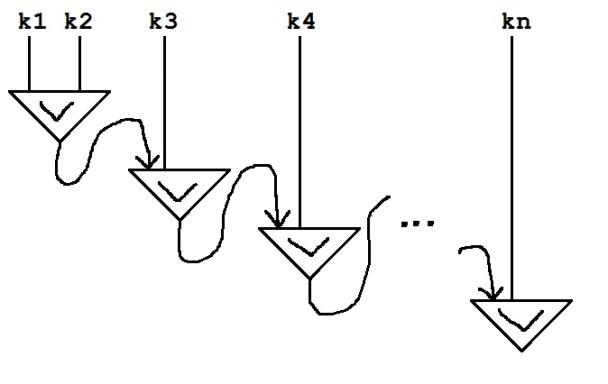
Обозначим полученную схему S, тогда

L(S) = L(Dn)+L(Vl)

L(Dn) = 2*2ⁿ + n – 4

l ≤ 2ⁿ

L(Vl)=l - 1≤ 2ⁿ – 1

L(S) ≤ (2*2ⁿ + n - 4) + (2ⁿ - 1) = 3*2ⁿ + n – 5.

БИЛЕТ 37

Реализация двоичного сумматора в классе схем из функциональных элементов.

*учебник*

{

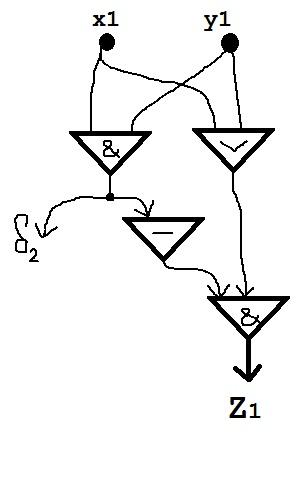
Определение. Сумматором S_n порядка n называется схема с 2n входами x₁, x₂, …, x_n, y₁, y₂, …, y_n и n + 1 выходом z₀, z₁, z₂, …, z_n такая, что |z| = |S_n(x,y)| = |x|+|y|.

Теорема. Существует схемный сумматор порядка n в базисе {˅, &, ̚ } с числом элементов 9n – 5. Доказательство. Построим искомый схемный сумматор. Для этого возьмём одну ячейку полусумматора, содержащую четыре элемента и n–1 ячейку сумматора, каждая из которых содержит девять элементов. Построим из этих частей сумматор.

}

*лекции*

Пусть имеются два числа, записанные в двоичном виде.

x =

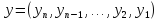
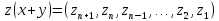
X1	Y1		Z1
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

xi	yi			zi
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	1	0
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

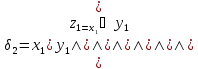
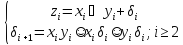
Блоки.

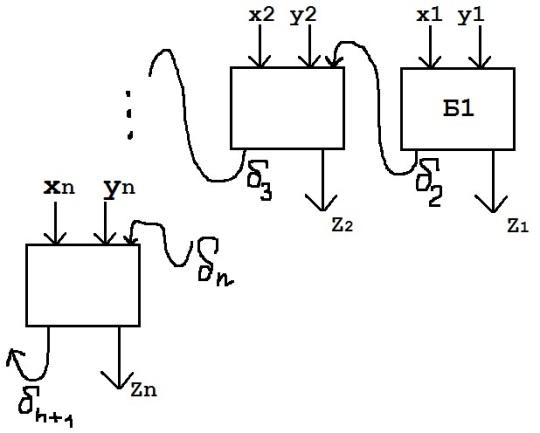
Блок Б1.

L(Б1)=4.

Бi, i

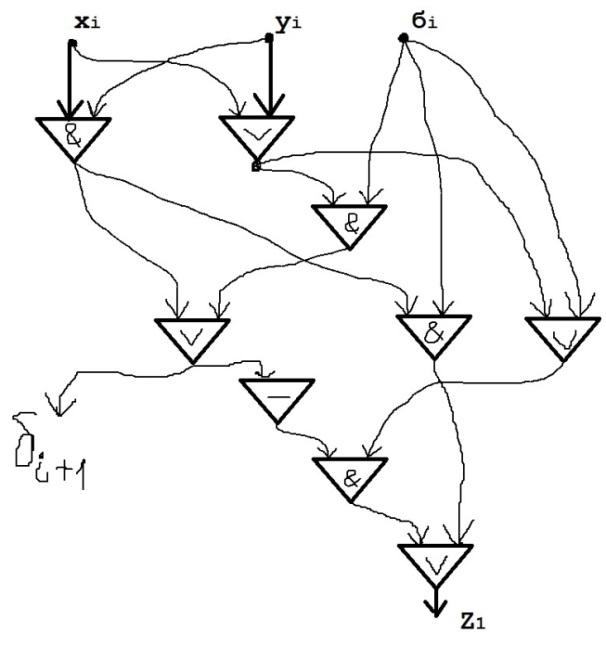
Сложность: L(Бi)=9.

L()=.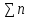

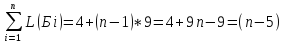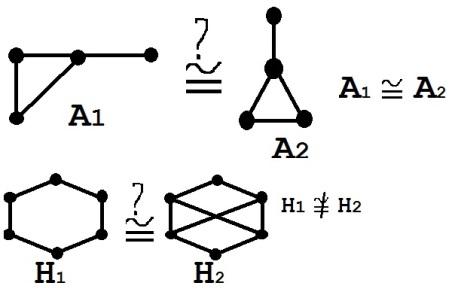
Теорема. Существует метод синтеза n-разрядного двоичного сумматора 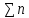такой, что L(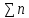)=9n-5.

БИЛЕТ 52

Примеры построения машин Тьюринга

Таблица управления машиной Тьюринга – распознавание симметрии.

qi\aj	0	1	˄	коммент.
q1	˄Rq2	˄Rq3	1Sq0
q20	0Rq2	1Rq2	˄Lq4
q3
q4	˄Lq5	˄Lq6	1Sq0
q5	0Lq5	1Lq5	˄Rq1
q6	˄Lq6	˄Lq6	0Sq0
q7	^Lq6	˄Lq5	1Sq0

БИЛЕТ 39

Логическое следствие.

Определение 1. Формула B называется логическим следствием формул A₁, A₂, …, A_n, если при любых значениях, входящих в них, элементарных высказываний формула B принимает значение истинно всякий раз, когда формулы A₁, A₂, …, A_n принимают значение истинно. Обозначается A₁, A₂, …, A_n ¦ B

Из определения логического следования вытекает:

Тавтология логически следует из любой формулы.

Из противоречия логически следует любая формула.

Теорема 1. Из A логически следует B тогда и только тогда, когда тавтологией является AB.

Теорема 2. A₁, A₂,…, A_n¦ B тогда и только тогда, когда является тавтологией

A₁&A₂& …& A_n B.

Теорема 3. Из формул A₁, A₂,…, A_n , B логически следует C тогда и только тогда, когда из формул A₁, A₂, …, A_n логически следует BC.

Следствие 1. Из A и B логически следует C тогда и только тогда, когда тавтологией является

A (BC).

Следствие 2. Из формул A₁, A₂, …, A_n логически следует B тогда и только тогда, когда тавтологией является

A₁ (A₂ … (A_nB)…).

Отношение логического следования играет в математике большую роль.

Если из A¦B, то A называется достаточным условием для B, а B - необходимым условием для A.

Если вместе с A¦B из B¦A, то A называется необходимым и достаточным условием для B, а B - необходимым и достаточным условием для A.

Определение. Формула  называется логическим следствием формул , если формула  превращается в истинное высказывание при всякой такой подстановке вместо всех ее пропозициональных переменных  конкретных высказываний, при которой в истинное высказывание превращаются все формулы . То, что формула  является логическим следствием формул , записывается так: . Формулы  называются посылками для логического следствия .

Таким образом, , если для любых высказываний  из

 следует .

Наконец можно и так сказать о логическом следствии. Составим таблицы истинности для формул . Предположим, что если в какой-то строке таблицы все формулы  принимают значение 1, то в этой строке непременно и формула  принимает значение 1. Это и будет означать, что  является логическим следствием формул .

Из сформулированного определения вытекает четкий алгоритм проверки формул на логическое следование (далее приводится в виде схемы). Рассмотрим его действие для случая, например, трех формул-посылок, зависящих от трех переменных:

Все эти формулы должны быть заданы таблицей своих значений:

БИЛЕТ 44

Изоморфизм графов. Необходимые условия изоморфизма графов.

*лекции*

Определение. Два графа G1=(V1,E1) и G2=(V2,E2) называются изоморфными, если существует взаимно-однозначное соответствие V1 и V2, сохраняющее отношение инцедентности.

Задачи в теории графов ставятся и решаются с точностью до изоморфизма графов.

Разновидности графов.

1. Ориентированный

Пример. Транспортные сети.

2. Мультиграфы – графы, в которых допускается несколько ребер одного направления.

3. Псевдографы – мультиграфы, в которых допускаются петли.

Степень – количество ребер инцедентных вершин.

Вершины степени 0 называются изолированными.

Вершина степени один называется висячей.

Маршрутом в графе G называется последовательность вершин и ребер.

M=(V0,e1,V1,e2,V2,…), где ei=(V_i-1,V_i) соединяет V_i-1 и Vi.

М=(V₀,V_k), где k-маршрута.

Граф называется связанным, если для любой пары вершин существует маршрут, соединяющий их.

БИЛЕТ 43

Способы задания графов.

*учебник*

{

Наиболее простым и естественным способом задания графа является графический. Однако таким образом можно задать только небольшие графы, к тому же он неудобен для автоматизированной обработки и передачи графической информации. Рассмотрим другие способы, используемые в теории графов.

В общем виде задать граф – значит описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер их достаточно занумеровать. Пусть – вершины графа ; – ребра. Отношение инцидентности может быть задано следующими способами:

1. Матрицей инцидентности размера . По вертикали и горизонтали указываются вершины и ребра соответственно, а на пересечении -й вершины и -го ребра, в случае неориентированного графа, проставляется 1, если они инцидентны, и 0 – в противоположном случае, т. е.

а в случае орграфа: –1, если вершина является началом дуги; 1 – если вершина является концом дуги и 0 – если вершины не инцидентны. Если некоторая вершина является для ребра и началом и концом (т. е. ребро – петля), проставляется любое другое число, например 2.

2. Списком ребер графа, представленным двумя столбцами: в левом перечисляются все ребра , в правом – инцидентные им вершины . Для н-графа порядок вершин произволен, для орграфа первым стоит номер начала дуги. При наличии в графе изолированных вершин они помещаются в конец списка.

3. Матрицей смежности – квадратной матрицей размера . По вертикали и горизонтали перечисляются все вершины, а на пересечении -й и -й вершин, в случае н-графа, проставляется число , равное числу ребер, соединяющих эти вершины. Для орграфа равно числу ребер с началом в -й вершине и концом в -й вершине.

}

*лекции*

Способы задания графов