1. Графический;

2. Перечислительный;

G = (V,E)

V = {V1,V2,V3,V4,V5}

E = {(V1,V2),(V2,V3),(V1,V4),(V2,V4)}

3. Матрица смежности;

Две вершины называются смежными, если они соединены некоторым ребром.

	V1	V2	V3	V4	V5
V1	0	1	0	1	0
V2	1	1	1	1	0
V3	0	1	0	0	0
V4	1	1	0	0	0
V5	0	0	0	0	0

4. Матрица инцеденций;

Строки – вершины, столбцы – ребра.

Пишем 1, если соответствующая вершина и ребро соединены, если нет, то 0.

	e1	e2	e3	e4
V1	1	0	1	0
V2	1	1	0	1
V3	0	1	0	0
V4	0	0	1	1
V5	0	0	0	0

5. Векторное задание;

e1 e2 e3 e4

V1 V2 V1 V2

V2 V3 V4 V4

6. Списки смежности;

V1: V2: V4;

V2: V1; V3; V4;

V3: V2;

V4: V1; V2;

V5: .

7. Структуры смежности

- компьютрное представление списков смежности.

БИЛЕТ 46

Планарные графы. Критерий планарности графов.

Говорят, что граф укладывается на плоскости, т. е. является планарным, или плоским, если его можно нарисовать так, что его ребра будут пересекаться лишь в концевых точках – вершинах. Изображение планарного графа на плоскости называется планарной укладкой. Определение планарности графов имеет большое практическое значение. Достаточно привести задачу разводки печатных плат, когда необходимо избежать пересечения проводников в местах, не предназначенных для соединений. Если изобразить места указанных соединений как вершины графа, то возникнет задача построения графа с непересекающимися ребрами. Важно отметить, что интерес представляет именно возможность построения графа с непересекающимися ребрами.

Графы Куратовского считаются основными непланарными графами потому, что играют решающую роль в исследовании планарности графов.

Рис. 3.21. Непланарные графы (графы Куратовского): a – граф ;

б – граф

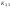
Теорема Понтрягина-Куратовского. Граф планарен тогда и только тогда, когда он не содержит в качестве подграфа графа или .

Утверждение: Полный граф K5 – не планарен.

Доказательство: допустим противное – граф K5 планарен и G есть его плоская укладка. Т.к. граф K5 и G изоморфны, то каждое ребро G есть 3-цикл. Положим n=3, p=5, q=10, получаем 10 ≤ 3*(5-2) / (3-2) = 9 ⇒ что противоречит условию ⇒ граф K5 – не планарен.

Утверждение: Граф K3,3 – не планарен.

Доказательство: допустим противное: граф K3,3 – планарен и имеет плоское изображение G, т.к. K3,3 и G изоморфны, то каждая грань в G есть 4-цикл. Подставляем в формулу следующие значения n=4, p=6, q=9, получаем 9 ≤ 4(6-2) / (4-2) = 8 ⇒ противоречие ⇒ K3,3 – не планарен.

БИЛЕТ 47

Деревья. Корневые деревья.

Деревом называется связный граф без циклов. Граф без циклов называется лесом.

Разновидности деревьев:

1.Корневые деревья. Выделение корня – разбиение дерева на ярусы и определение ориентации ребер от корня. Используется понятие сыновей и потомков.

2.Упорядоченные деревья. Для каждой вершины задается порядок среди смежных с ней вершин.

3.Бинарные деревья. У каждой вершины либо нет сыновей, либо 2 сына, либо 1.

Элементарные свойства деревьев:

1.Удаление висячей вершины в дереве приводит снова к дереву.

2.При добавлении любого ребра к дереву соединяющего вершину образуется цикл.

3.В любом не тривиальном дереве имеется по крайней мере 2 висячие вершины.

4.Для любого дерева T : q(T)=P(T)-1.

Из другого источника:

Определение 1. Любое дерево, в котором выделена одна вершина, называемая корнем,

называется корневым деревом.

Определение 2. 1) Граф, состоящий из одной вершины, которая выделена, называется

корневым деревом.

2) Пусть имеются корневые деревья D₁, D₂, …, D_m с корнями v₁, v₂, …, v_m, D_i = (V_i, E_i),

V_i∩ V_j= ∅ (i ≠ j). Тогда граф D = (V, E), полученный следующим образом:

V = V₁ ∪ V₂ ∪ … ∪ V_m ∪ {v} (v ∉ V_i, ∀_i ), E = E₁ ∪ E₂ ∪ … ∪ E_m ∪ {(v, v₁), (v, v₂), …,(v, v_m)}

и в котором выделена вершина v, называется корневым деревом.

3) Только те объекты являются корневыми деревьями, которые можно построить со-

гласно пунктам 1) и 2).

При таком определении D₁,D₂,…,D_m называются поддеревьями дерева D.

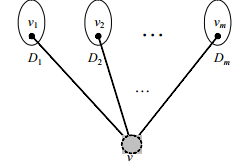
Определение 3. Упорядоченным корневым деревом называется корневое дерево, в котором

1) задан порядок поддеревьев и

2) каждое поддерево Di является упорядоченным поддеревом.

Дерево с одной вершиной также является упорядоченным поддеревом.

БИЛЕТ 48

Задачи о кратчайших путях в графах.

Алгори́тм Де́йкстры (англ. Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.

Неформальное объяснение

Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.

Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.

БИЛЕТ 49

Задача о минимальном остовном дереве.

Постановка задачи

Итак, имеется n городов, которые нужно объединить в единую телефонную сеть. Для этого достаточно проложить (n-1) телефонных линий между городами. Как соединить города так, чтобы суммарная стоимость соединений (телефонного кабеля) была минимальна?

В общем случае, задачу можно сформулировать так. Пусть дан связный, неориентированный граф с весами на ребрах G(V, E), в котором V — множество вершин (контактов), а E — множество их возможных попарных соединений (ребер). Пусть для каждого ребра (u,v) однозначно определено некоторое вещественное число w(u,v) — его вес (длина или стоимость соединения). w() называется весовой функцией. Задача состоит в нахождении такого связного ациклического подграфа T ⊂ G, содержащего все вершины, что суммарный вес его ребер будет минимален.

Так как T связен и не содержит циклов, он является деревом и называется остовным или покрывающим деревом (spanning tree). Остовное дерево T, у которого суммарный вес его ребер w(T) = ∑_(u,v)∈T w(u,v) минимален, называется минимальным остовным или минимальным покрывающим деревом (minimum spanning tree).

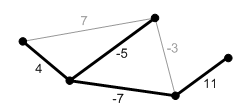
Рис.

Суммарный вес дерева = 37. Это минимальное остовное дерево не уникально: удалением ребра (c,d) и добавлением ребра (a,b) получается новое минимально остовное дерево.

Так как рассматриваются только деревья, можно считать все ребра положительными (достаточно добавить к весу всех ребер некоторую относительно большую положительную константу). В противном случае, если стоимость соединения между двумя вершинами равна отрицательному числу, можно несколько раз параллельно соединить их для уменьшения суммарного веса остовного подграфа.

Суммарный вес равен 3.

Суммарный вес равен 0.

Также считаем, что для любой пары ребер их весовые характеристики будут различны. Это гарантирует уникальность построенного минимального остовного дерева. Для примера, если все ребра имеют единичный вес, то любое остовное дерево будет минимальным (с суммарным весом v-1, где v – количество вершин в графе).

Все возможные минимальные остовные деревья для данного графа.

В данном случае, любой алгоритм построит одно из минимальных остовных деревьев. Один из вариантов разрешения неопределенности заключается в модификации алгоритма сравнения ребер по весу, например, так:

SHORTER-EDGE(i;j;k;l) 1: if w(i,j) < w(k,l) then return (i,j) 2: if w(i,j) > w(k,l) then return (k,l) 3: if min(i,j) < min(k,l) then return (i,j) 4: if min(i,j) > min(k,l) then return (k,l) 5: if max(i,j) < max(k,l) then return (i,j) 6: return (k,l)

БИЛЕТ 51

Машины Тьюринга.

Долгое время неформальное понятие алгоритма удовлетворяло потребности.

В начале 20в. появилась необходимость уточнения (формализации) понятия. Практически одновременно появилось несколько формализаций. Одной из них было понятие «Машины Тьюринга» (англ. математик Алан Тьюринг (1936-1037гг)) – М.

М состоит из составных частей

1. Пишущая читающая лента;

2. Пишущая читающая головка;

3. Устройство управления;

4. Программа.

Имеется конечный рабочий алфавит А.

А = {a₀, a₁, …, a_n-1}.

Символ а₀ = ˄ - квантовый (особый) символ, символ пробела.

Лента разбита на ячейки и бесконечна в обе стороны.

В каждый момент времени в каждой ячейке ленты записан ровно 1 символ из алфавита А. В каждый момент времени читающая головка обозревает ровно одну ячейку ленты. В каждый момент времени устройство управления находится ровно в одном из состояний (их всего Q).

Q = {q₀, q₁, …, q_n-1}, q₁ – начальное состояние, q₀ - стоп-состояние.

Программа состоит из команд, каждая команда имеет вид:

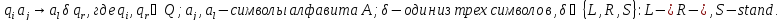
М работает по такту в дискретном времени: t = 1, 2, 3 … .

На каждом такте выполняется одна команда. Пусть в некоторый момент времени t УУ находится в состоянии q_i, а головка обозревает ячейку, в которой записан символ a_j, тогда выполняется q_ia_j … .

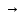Замечание. В программе не должно быть двух разных команд с одной и той же первой частью.

Выполнение команды заключается в том, что символ a_j стирается и на его место записывается a_l; головка сбивается на одну ячейку влево или вправо, либо остается на месте в зависимости от 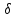; и к моменту времени t+1 УУ переходит в состоянии q_r функционирование М прекращается, когда УУ перейдет в стоп-состояние (q₀).

Машина Тьюринга M вычисляет словарную функцию

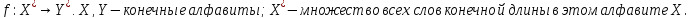
Берем x=x₁,x₂, …,x_n ϵ X*.

Пусть f(x)=y₁,y₂, …y_p , тогда M должна, начиная со стандартной начальной конфигурации со словом Х, перейти в заключительную стандартную конфигурацию со словом У.

Если f(x) не определена, то М не должна останавливаться.

Т.е. было

стало:

Т.

1) Говорят, что словарная функция 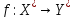вычислима по Тьюрингу, если существует машина Тьюринга, вычисляющая эту функцию (мы работаем не с числами, а с их изображением).

2) А – конечный алфавит, что связано с ограничением на выпускающую (разрешающую) способность.

3) Q – конечное (количество состояний).