
Мат. анализ, 1 часть; 1 семестр(1)
.pdf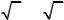
т.е.
f (x)~g(x) при x *.
Теорема доказана.
Теорема. Сумма бесконечно малых (бесконечно больших) различного порядка малости эквивалентна слагаемому низшего порядка малости (высшего порядка роста).
Доказательство. Пусть (x) |
и (x) б.м. (б.б.) при x *, причем o( ). Тогда |
|||||||
|
(x) (x) |
|
(x) |
|
|
(x) |
1. |
|
lim |
lim 1 |
|
1 lim |
|||||
(x) |
(x) |
|
||||||
x * |
x * |
|
x * (x) |
|||||
Следовательно,
(x) (x)~ (x) при x *.
Теорема доказана.
Нетрудно убедиться, что эта теорема справедлива для любого конечного числа слагаемых.
Пример. x3/2 2 x ~2 x |
при x 0 |
|
|
|
|
|
|
|
|
|
x являются |
|||||||||||||
Соотношения эквивалентности |
для многочлена |
|
при x 0 |
или при |
||||||||||||||||||||
следствиями доказанной теоремы. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Теорема. Предел отношения двух бесконечно малых (двух бесконечно больших) |
||||||||||||||||||||||||
функций не изменится при замене этих функций на эквивалентные, т.е. |
|
|
|
|||||||||||||||||||||
если f (x)~ f0(x) |
при x *, а g(x)~g0(x) при x *, то |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
lim |
f (x) |
lim |
f0(x) |
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Доказательство. |
|
x * g(x) |
x * g0(x) |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
f (x) |
lim |
f (x) |
|
g0 (x) |
|
f0(x) |
lim |
f (x) |
lim |
g0(x) |
lim |
f0(x) |
lim |
f0(x) |
. |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
x * g(x) |
x * f0(x) g(x) |
|
g0(x) x * f0(x) x * g(x) |
x * g0(x) |
x * g0(x) |
|||||||||||||||||||
Теорема доказана.
§6. Использование соотношений эквивалентности для вычисления пределов и асимптотического сравнения функций.
Последняя теорема, вместе с таблицей эквивалентных функций, является основой наиболее удобного и широко используемого метода вычисления пределов.
Пример. Найдем предел
lim |
ln(1 x2) (sin x)2 |
. |
|
|
|
|
|
|
|
5x4 x6 |
|
|
|
|
|
|
|
||
x 0 |
|
|
|
|
|
|
|
|
|
Поскольку при x 0 ln(1 x2)~x2 |
(ln(1 t)~t |
при t 0, |
t x2 ), sinx ~x, 5x4 x6 ~5x4 , |
||||||
то |
|
|
|
|
|
|
|
|
|
|
ln(1 x2) (sin x)2 |
|
x2 |
x2 |
1 |
|
|
|
|
lim |
|
lim |
|
|
|
|
. |
|
|
5x4 x6 |
|
|
|
|
|
||||
x 0 |
x 0 5x4 |
5 |
|
|
|
||||
Соотношения эквивалентности (табл. 1) удобно также использовать для асимптотического сравнения функций.
Пример. Предел
|
|
0 |
|
|
|
|
|
x2 |
|
|
|
|
|
ln(cosx) |
|
|
ln(1 (1 cosx)) |
1 cosx |
|
1 |
|
||||
|
0 |
. |
||||||||||
lim |
|
lim |
|
lim |
|
lim |
|
|
|
|||
x2 |
x2 |
|
|
|
||||||||
x 0 |
|
|
x 0 |
x 0 x2 |
x 0 2x2 |
2 |
|
|||||
41
Здесь использованы соотношения эквивалентности ln(1 t)~t при t 0 (t 1 cosx) и
1 cosx ~ |
x2 |
при x 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Пример. Предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
lim |
e |
x |
|
1 |
|
lim |
2/ x |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
x 1/ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Здесь использованы соотношения эквивалентности et |
1~t |
при t 0 |
(t |
, очевидно, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
что при x t 0) и tgt ~t при t 0 t |
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Пример. Предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
cos |
|
|
|
0 |
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
y |
|
1 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
lim |
|
|
2 |
|
|
lim |
|
|
|
|
|
|
|
|
|
lim |
2 |
|
|
lim |
|
. |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
x x |
|
|
|
|
y 0 |
|
|
|
|
|
|
y 0 |
y |
|
|
|
|
|
|
|
y 0 2y |
2 |
y 0 при |
x ), формула |
||||||||||||||||||||||||||||||||
Здесь использована замена переменной |
y x (x y , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
приведения |
cos |
|
|
|
|
sin и соотношение |
эквивалентности sint~t |
при t 0 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
t |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пример. Предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
limex2 ln(cosx) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
lim(cosx)x2 |
|
limeln(cosx)x2 |
e |
2 |
, |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
т.к. |
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ln(cosx) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
x 0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
(см. выше) и на основании теоремы о пределе сложной функции (внутренняя функция
y |
ln(cosx) |
, внешняя – |
g(y) ey ). Здесь использован тот факт, что любое |
|
x2 |
||||
|
|
|
положительное число a можно представить в виде a elna (т.к. экспонента и натуральный логарифм – взаимно-обратные функции).
Вообще, при x x0 |
|
0 , удобно использовать замену переменной y x x0 . |
|||||||||||||||||||||||||||||||||
Пример. Найдем порядок малости функции |
|
f (x) относительно функцииg(x), где |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
g(x) 1 |
1 |
|
|
1, x . |
||||||||||||||||||||||
f (x) 2ln 1 sin |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
|
x |
4 |
x |
3 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Видим, что при x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
1 |
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
f (x)~2sin |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
~ |
|
|
, а |
|
|
|
|
|
|
|
|
||||||||
|
2 |
x |
4 |
|
|
x |
2 |
x |
4 |
x |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
g(x)~ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поэтому порядок малости |
|
f (x) |
|
относительно g(x) |
при k |
. |
|||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
Действительно,
42

|
f (x) |
|
2 |
|
|
1 |
x |
3 |
|||
lim |
lim |
x2 |
|
lim |
2 |
|
. |
||||
|
|
|
|
|
|
2 |
|
||||
x g |
(x) |
x 12x3 |
x |
x |
|
|
|||||
|
|
|
|
|
|||||||
Очевидно, что этот предел не равен ни нулю, ни бесконечности только при 2 (при
3
2 он равен , а при 2 - нулю). 3 3
Вообще, как при вычислении пределов, так и при асимптотическом сравнении функций, эквивалентная функция обычно ищется в одном из указанных в приведенной ниже таблице видов, в зависимости от стремления аргумента и функции (везде подразумевается, что 0).
|
x 0 |
x |
x x0 |
f (x) 0 |
f (x)~Cx |
f (x)~C / x |
f (x)~C(x x0) |
f (x) |
f (x)~C / x |
f (x)~Cx |
f (x)~C /(x x0) |
Эквивалентная не всегда существует в таком виде, но если существует, то единственна.
Опр. Пусть б.м. (б.б.) |
функции f (x) и g(x) |
определены в некоторой проколотой |
|
|
представима в виде |
|
|
окрестности u (*). Если f (x) |
|
||
f (x) g(x) o(g(x)), x *, |
|
|
|
то g(x) называется главной частью функции |
f (x) |
при x *. Не трудно показать, что |
|
g(x) является главной частью функции f (x), |
тогда и только тогда, когда f (x)~g(x) |
||
(при рассматриваемом стремлении аргумента). |
|
|
|
Лекция 6
§ 1. Понятие непрерывности функции в точке.
Опр. Функция f(x), определенная в некоторой (не проколотой!) окрестности точки
x0 называется непрерывной в этой точке,если: |
|
|
|
|
|
|
|||
1) существует lim |
f (x) ; |
|
|
|
|
|
|
||
|
|
x x0 |
|
|
|
|
|
|
|
2) этот предел равен значению функции в точке x0 . |
|
|
|
|
|||||
Класс (множество) функций, непрерывных в точке |
x0 |
обозначается |
C(x0). |
||||||
Соответственно, факт непрерывности функции в |
точке |
x0 |
можно записать |
в виде: |
|||||
f (x) C(x0). Итак, по определению |
|
|
|
|
|
|
|||
|
|
|
{f (x) C(x )} df |
{lim |
f (x) f (x )}. |
|
|
||
|
|
|
0 |
x x0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Так функция |
y x2 |
является непрерывной в точке |
x 0 |
(как и во всех других |
|||||
точках вещественной оси), |
рис. 1. Действительно, при x достаточно близких к нулю, эта |
||||||||
функция будет сколь угодно близка к нулю, но y(0)=0. |
|
|
|
|
|||||
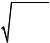
Функция, график которой представлен на рис. 2, не является непрерывной в точке |
|||||||||
x0 . Действительно, |
эта функция имеет различные пределы при x x0 и при |
x x0 |
|||||||
( f (x0 ) и |
f (x0 ), |
соответственно). Поэтому |
двустороннего |
предела при x x0 не |
|||||
существует. |
|
|
|
|
|
|
|
|
|
43
Рис. 1. График функции y x2 .
Рис. 2. Пример функции, не являющейся непрерывной.
Для понимания смысла непрерывности, полезна следующая иллюстрация: функция непрерывна, если ее график можно нарисовать, не отрывая ручки от листа.
С учетом определения предела, определение непрерывности функции можно дать в более развернутой (более подробной) форме:
Опр. Функция f (x), определенная в некоторой окрестности точки x0 называется непрерывной в этой точке, если в достаточно малой окрестности точки x0 значения этой функции сколь угодно близки к f (x0):
f (x) C(x0) df 0 0: x u (x0) | f (x) f (x0 )| .
С учетом теоремы о связи двустороннего предела с односторонними, определение непрерывности функции в точке можно дать также в следующей (равносильной предыдущим) форме.
Опр. Функция f(x), определенная в некоторой окрестности точки x0 называется непрерывной в этой точке, если:
44

1) существует |
lim |
f (x) ; |
|
|
|||
|
|
x x0 |
|
|
|
|
|
2) существует |
lim |
f (x) ; |
|
|
|||
|
|
x x0 |
|
|
|
|
|
3) lim |
f (x) |
lim |
f (x) |
f (x0 ) . |
|
||
x x0 |
|
|
x x0 |
|
|
|
|
Еще одну (эквивалентную предыдущим) формулировку определения |
|||||||
непрерывности можно дать в терминах приращений. |
|
||||||
Пусть функция |
f (x) |
определена в некоторой окрестности точки x0 . |
Выберем |
||||
какое-нибудь |
значение |
|
x |
из этой |
окрестности и назовем разность |
x x x0 |
|
приращением аргумента. Отметим, что приращение аргумента может быть как положительным, так и отрицательным. Соответствующую разность y f (x) f (x0)
назовем приращением функции (рис. 3).
Рис. 3. Иллюстрация понятия приращения функции.
Опр. Функция f (x) называется непрерывной в точке x0 если бесконечно малому
приращению аргумента в этой точке соответствует бесконечно малое приращение функции:
{f (x) C(x0)} df {lim y 0}.
x 0
Эквивалентность этой формулировки определения непрерывности самой первой формулировке, очевидна из того факта, что x 0 тогда и только тогда, когда x x0 , а
y 0 тогда и только тогда, когда f (x) f (x0).
Итак, в настоящем параграфе дано четыре равносильных формулировки определения непрерывности функции в точке.
§ 2. Понятие односторонней непрерывности.
Рассмотрим функцию y 
 x . Бессмысленно говорить о том непрерывна ли она в точке x=0, поскольку она определна только при x 0. Однако можно ввести понятие правосторонней непрерывности.
x . Бессмысленно говорить о том непрерывна ли она в точке x=0, поскольку она определна только при x 0. Однако можно ввести понятие правосторонней непрерывности.
Опр. Функция f (x), определенная в правосторонней окрестности точки x0
называется правосторонне-непрерывной в этой точке (непрерывной в точке x0 справа),
если существует предел данной функции при x x0 и он равен значению функции в точке x0 :
lim f (x) f (x0 ).
x x0
Нетрудно видеть, что функция y 
 x является правосторонне-непрерывной в точке x0 .
x является правосторонне-непрерывной в точке x0 .
Аналогично определяется левосторонняя непрерывность.
45
Опр. Функция f (x), определенная в левосторонней окрестности точки x0
называется левосторонне-непрерывной в этой точке (непрерывной в точке x0 слева), если существует предел данной функции при x x0 и он равен значению функции в точке x0 :
lim f (x) f (x0).
x x0
Теорема. Для того, чтобы функция f (x) была непрерывна в точке x0, необходимо и достаточно, чтобы она была непрерывна в этой точке, как слева, так и справа.
Справедливость этой теоремы очевидна из теоремы о связи двустороннего предела функции с односторонними.
§3. Арифметические операции над непрерывными функциями.
Теорема. Сумма функций, непрерывных в точке x0, есть функция непрерывная в этой точке.
Доказательство. Пусть функции f (x) и g(x), определенные в некоторой
окрестности точки x0 непрерывны в этой точке. По определению непрерывности (первая формулировка) это означает, что
lim f (x) f (x0) и lim g(x) g(x0). |
|
||
x x0 |
|
x x0 |
|
Значение функции (x) f (x) g(x) в точке x0 |
очевидно равно (x0) f (x0) g(x0). |
||
В силу теоремы о пределе суммы, существует |
|
||
lim (x) lim |
f (x) lim g(x) f (x0) g(x0) (x0), |
||
x x0 |
x x0 |
x x0 |
|
что и означает непрерывность функции (x) в точке x0 .
Теорема доказана.
Очевидно, что эта теорема справедлива для любого конечного числа слагаемых. Аналогично доказываются две следующие теоремы.
Теорема. Произведение функций, непрерывных в точке x0, есть функция непрерывная в этой точке.
Следствие. Произведение непрерывной функции на число – функция непрерывная. Действительно, число (т.е. постоянная) есть функция непрерывная на R .
Теорема. Частное двух функций непрерывных в точке x0 есть функция непрерывная в этой точке, при условии, что делитель (функция, стоящая в знаменателе) не равен нулю.
§4. Переход к пределу под знаком непрерывной функции. Непрерывность сложной функции (композиции функций).
Теорема. Пусть функция z g(y) непрерывна в точке y0 , а функция, y f (x)
имеет конечный предел при x x0 равный y0 :
lim f (x) y0 .
x x0
Тогда
lim g(f (x))
x x0
g(lim f (x))
x x0
Доказательство.
Поскольку g(y) непрерывна в точке y0,
46
lim g(y) g(y0).
y y0
По условию теоремы, существует также
lim f (x) y0 . Но, по теореме о пределе сложной функции, из этих двух фактов вытекает,
x x0
что
lim g(f (x)) g(y0) g |
lim f (x) |
|
. |
|
|
x x0 |
x x0 |
|
|
|
|
Теорема доказана. |
|
|
|
|
функции). Пусть функция y f (x) |
Теорема (о непрерывности сложной |
|||||
непрерывна в точке x0 , а функция g(y) |
непрерывна в точке y0 , причем y0 f (x0). Тогда |
||||
сложная функция F(x) g( f (x)) непрерывна в точке x0 . |
|||||
Доказательство. Поскольку функция f (x) |
непрерывна в точке x0 , |
||||
lim f (x) f (x0). |
|
|
|
|
|
x x0 |
|
|
|
|
|
Но, в силу предыдущей теоремы,
lim F(x) lim g(f (x)) g |
lim f (x) |
|
g(f (x0)) |
|
x x0 |
x x0 |
x x0 |
|
|
что и означает непрерывность функции F(x) g( f
F(x0),
(x)) в точке x0 .
Теорема доказана.
§5. Локальные свойства функции, непрерывной в точке.
Теорема. Если функция f (x) непрерывна в точке x0 и f (x0) 0, то существует окрестность u (x0 ), в которой знак функции совпадает с ее знаком в точке x0 .
Доказательство. . Поскольку функция f (x) непрерывна в точке x0 ,
lim f (x) f (x0).
x x0
В силу теоремы о сохранении функцией знака предела, существует окрестность u (x0 ), в которой знак функции совпадает со знаком f (x0).
Теорема доказана.
Данная теорема проиллюстрирована на рис. 4. Очевидно, что раз непрерывная функция положительна в точке x0 , то она останется положительной и в некоторой (хотя бы малой)
окрестности этой точки.
Рис. 4. Иллюстрация сохранения знака непрерывной функцией.
47

Теорема. Функция, непрерывна в точке x0, локально ограничена в этой точке. Справедливость этой теоремы вытекает из теоремы о локальной ограниченности функции, имеющей предел и определения непрерывности. Доказательство опустим.
Лекция 7
§1. Непрерывность функции на промежутке.
Опр. Функция f (x), определенная на интервале (a,b) называется непрерывной на этом интервале, если она непрерывна в каждой его точке.
Опр. Функция f (x), определенная на полуинтервале [a,b), называется непрерывной на этом полуинтервале, если она
1.непрерывна на интервале (a,b);
2.правосторонне непрерывна в точке a.
Опр. Функция f (x), определенная на полуинтервале (a,b], называется непрерывной на этом полуинтервале, если она
1.непрерывна на интервале (a,b);
2.левосторонне непрерывна в точке b .
Опр. Функция f (x), определенная на отрезке [a,b], называется непрерывной на этом отрезке, если она
1.непрерывна на интервале (a,b);
2.правосторонне непрерывна в точке a.
3.левосторонне непрерывна в точке b .
Пример. Функция y 
 1 x2 непрерывна на отрезке x [ 1,1].
1 x2 непрерывна на отрезке x [ 1,1].
Класс (множество) функций, непрерывных на промежутке X обозначается C(X). Соответственно, факт непрерывности функции на промежутке X можно записать в виде: f (x) C(X). Например, если функция непрерывна на интервале (a,b), то f (x) C(a,b).
§2. Непрерывность элементарных функций.
Справедлива следующая теорема.
Теорема. Основные элементарные функции непрерывны в области определения. Эта теорема доказывается для каждой из основных элементарных функций (степенной, показательной, логарифмической, тригонометрических и обратных тригонометрических) по отдельности, на основе определения непрерывности функции в точке.
В качестве примера, докажем, что функция y sin x непрерывна на R . Очевидно,
что она является непрерывной в точке x 0: limsin x sin0 0, т.е. при xдостаточно
x 0
близких к нулю, значения этой функции будут сколь угодно близки к нулю. Рассмотрим произвольную точку x0 R . Приращению x аргумента в этой точке отвечает приращение функции
48
y sin(x |
|
x) sin x |
2sin |
x |
cos(x |
|
x |
). |
|
|
|
|||||||
|
|
|
|
|
||||||||||||||
|
0 |
|
|
x |
|
|
0 |
2 |
0 |
2 |
|
|
|
|
||||
Функция 2cos(x |
|
) ограничена на R : |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|2cos(x |
x |
)| 2, |
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а функция sin |
x |
|
– б.м. при x 0, |
по теореме о пределе сложной функции и в силу |
||||||||||||||
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
того, что |
limsin x 0. |
По |
теореме |
о произведении |
б.м. |
функции на |
локально |
|||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ограниченную, y 0 |
при |
x 0, |
а последнее и означает непрерывность функции |
|||||||||||||||
y sin x в |
точке x0 . |
В |
силу произвольности выбора |
точки |
x0 , функция |
y sin x |
||||||||||||
непрерывна на R . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Как уже говорилось в лекции 2, элементарной функцией называется любая функция, полученная из основных элементарных функций и постоянных с помощью арифметических операций (сложения, умножения и деления), а также композиции (построения сложной функции).
Теорема. Элементарные функции непрерывны в области определения.
Справедливость этой теоремы очевидна из предыдущей теоремы и теорем о непрерывности суммы, произведения, отношения и композиции непрерывных функций. В качестве примера докажем непрерывность многочлена.
Многочлен Pn (x) c0 c1x ... cnxn определен на R . Покажем, что он непрерывен на
R . Очевидно, что постоянная y c |
есть непрерывная на R функция: для любого x R и |
для любого x |
|
y c c 0,
а следовательно при x 0 y 0.
(Впрочем, для того чтобы убедиться в непрерывности постоянной, достаточно изобразить
ее график). |
Функция y x тоже непрерывна на R : |
|
|
|
|
||||||||
y x, следовательно, при x 0 |
y 0. |
|
|
|
|
|
|||||||
Функция |
y x2 |
x x непрерывна |
на |
R , |
как |
произведение непрерывных |
функций. |
||||||
Следовательно, |
непрерывна |
и |
функция |
y x3 |
x2 x и |
т.д., вплоть |
до |
функции |
|||||
y xn xn 1 x. |
Функции |
y c |
|
xk |
(k 0,1,...,n) |
тоже |
непрерывны |
на |
R , как |
||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
произведения двух непрерывных функций. Наконец, |
многочлен Pn (x) непрерывен на R , |
||||||||||||
как сумма непрерывных функций. |
|
|
|
|
|
|
|
|
|
|
|||
Теорема о непрерывности элементарных функций играет важнейшую роль для вычисления пределов. Действительно, именно из нее по определению непрерывности
следует, что если элементарная |
функция |
y f (x) |
определена |
в точке |
x0 , то |
||||||||||||
lim |
f (x) f (x0), чем мы постоянно пользуемся при |
вычислении |
пределов, |
заменяя |
|||||||||||||
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
предел функции на ее значение в предельной точке (см. лекцию 3). Например, |
|
||||||||||||||||
|
lim |
tgx |
lim |
sin x |
lim |
sin x |
lim |
1 |
1 1 1. |
|
|
|
|
||||
|
|
xcosx |
|
|
|
|
|
|
|||||||||
|
x 0 x |
|
x 0 |
x 0 x |
x 0 cosx |
|
|
|
|
|
|
|
|||||
lim |
sin x |
1, |
как первый |
замечательный предел, |
а lim |
|
1 |
1, поскольку значение этой |
|||||||||
|
|
|
|||||||||||||||
x 0 |
x |
|
|
|
|
|
|
|
|
x 0 cosx |
|
|
|||||
функции в предельной точке равно единице.
49
§3. Классификация точек разрыва.
Опр. Пусть функция f (x) определена в некоторой проколотой окрестности точки
x0 . И пусть она непрерывна в любой точке этой окрестности, но не является непрерывной в самой точке x0 . В этом случае, точка x0 называется точкой разрыва функции f (x).
При классификации точек разрыва, будем отталкиваться от второй формулировки определения непрерывности функции в точке:
функция f (x) называется непрерывной в точке x0 , если существуют оба односторонних предела данной функции в этой точке, причем
lim |
|
f (x) |
lim |
f (x) f (x0 ) . |
x x0 |
|
x x0 |
|
|
Выделим несколько случаев нарушения указанных условий. |
||||
Опр. Если x0 – точка разрыва функции f (x), но существуют (конечные) пределы |
||||
lim |
|
f (x) |
f (x0 |
) и lim f (x) f (x0 ), |
x x0 |
|
|
x x0 |
|
точка x0 называется точкой разрыва первого рода.
Можно выделить два подкласса таких точек разрыва.
Опр. Если f (x0 ) f (x0 ), точка разрыва первого рода x0 называется точкой
конечного разрыва (точкой скачка). При этом разность f (x0 ) f (x0 ) называется
скачком функции в точке x0.
Пример точки конечного разрыва представлен на рис. 2 лекции 6.
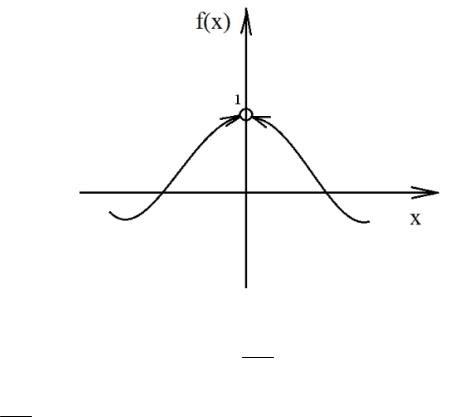
Опр. Если f (x0 ) f (x0 ) f (x0), в частности, если f (x0) не определено, точка разрыва первого рода x0 называется точкой устранимого разрыва.
Рис. 1. Пример точки устранимого разрыва.
Пример. Рассмотрим функцию f (x) sin x (рис. 1). Эта функция не определена в x
точке x 0. Но, как известно,
limsin x 1
x 0 x
50
