
Мат. анализ, 1 часть; 1 семестр(1)
.pdf
§8. Основные элементарные функции. Класс элементарных функций.
В курсе математического анализа 1-ого семестра мы ограничимся изучением отображений R→R. Важнейшими из этих отображений являются элементарные функции.
Для построения класса элементарных функций определим сначала основные
элементарные функции. К основным элементарным функциям относятся: |
|
||
Степенные функции: y x |
|
|
|
Показательные функции: y ax |
|
|
|
Логарифмические функции y loga x |
|
|
|
Тригонометрические функции y sin x , |
y cosx |
y tgx, y ctgx |
|
Обратные тригонометрические функции y arcsin x, y arccosx, y arctgx, |
y arcctgx |
||
Опр. Элементарной функцией называется функция, построенная из основных элементарных функций и постоянных с помощью операций сложения, умножения и деления, а также композиции (построения сложной функции).
1
Пример. Функции y 2e , y arctgx4 являются элементарными функциями. Отображения R→R не ограничиваются элементарными функциями.
Приведем также примеры функций, не являющихся элементарными. Пример. Функция y sign(x), определенная равенством
1, |
x 0; |
|
sign(x) |
|
, |
1, |
x 0 |
|
Рис.13. График функции y signx .
называемая сигнатурой (рис. 13). Она является отображением R→R, но не относится к классу элементарных функций.
Пример. Другим примером неэлементарной функции служит функция «целая часть» y [x] – отображение, ставящее в соответствие вещественному числу результат его округления до ближайшего целого в меньшую сторону. Так
[10.8]=10, а [ 2.7] 3.
§9. Понятие числовой последовательности.
Рассмотрим бесконечное упорядоченное множество вещественных чисел, элементы которого пронумерованы натуральными числами (индексами n 1,2,3,...):
{xn} x1,x2,...,xn,...
11

Такое множество называется числовой последовательностью, а его элементы xi – членами числовой последовательности (Рис. 14).
Примеры.
1) {3n}=3, 6, 9, 12, 15…
2) {2n}=2, 4, 8, 16…  3) {1}=1, 1, 1, 1, 1… Рис. 14. Числовая последовательность. 4) {
3) {1}=1, 1, 1, 1, 1… Рис. 14. Числовая последовательность. 4) {




 }=1, -1, 1, -1, 1…
}=1, -1, 1, -1, 1…
Отметим, что последовательность – частный вид функции, а именно – функция N→R, т.е. отображение с областью определения на множестве натуральных чисел и областью значений на множестве вещественных чисел: x=f(n).
Задать последовательность – значит указать правило, позволяющее по номеру n находить значение 
 . Обычно последовательность задается формулой вида xn f (n). Например,
. Обычно последовательность задается формулой вида xn f (n). Например,
x |
|
1 |
. Можно также задать последовательность с помощью рекуррентной формулы. |
|
2n |
||||
n |
|
|
Простейшая рекуррентная формула выражает каждый следующий член последовательности через предыдущий: xn 1 f (xn ). При этом нужно дополнительно задать первый член последовательности x1 . Например, условия
x1 1, xn 1 2xn, n 1,2,3,...
задают последовательность 1,2,4,8,… .
Понятие ограниченной (сверху или снизу) числовой последовательности вводится также как для числового множества (поскольку последовательность – частный случай множества).
Лекция 2
§1. Предел числовой последовательности.
Говорят, что числовая последовательность {xn} имеет предел, равный a:
lim xn a ,
n
если все члены этой последовательности с достаточно большими номерами сколь угодно близки к числу a.
В качестве примера, рассмотрим последовательность, представленную на рис. 1. Первый элемент последовательности x1 выбирается произвольно. Второй элемент x2
выбирается делением отрезка [x1,a] пополам. Третий элемент – делением отрезка [x2,a]
пополам и т.д.
Рис. 1. Предел числовой последовательности.
Дадим теперь точное определение предела.
12
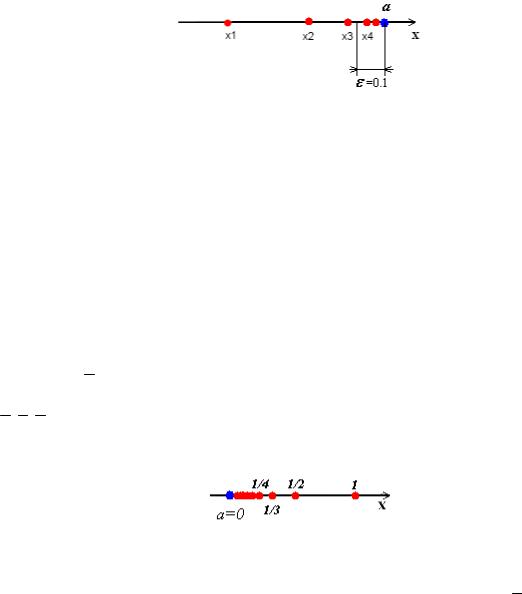
Опр. Число a называется пределом числовой последовательности {xn} при n ,
если для любого, сколь угодно малого, положительного числа найдется такое, достаточно большое, натуральное число N , что при n N выполняется неравенство
| xn a| :
{limxn a} df { 0 N : n N | xn a| }.
n
Рис. 2. Предел числовой последовательности. |
|
|
|
Так, на рис. 2 показано, что если выбрать 0.1, все |
члены рассмотренной |
выше |
|
последовательности с номерами n N 3 отличаются от |
a меньше, чем на |
(т.е. |
|
| xn a| ). Если же выбрать в сто раз меньше, чем показано на рис. 2, |
то, все-равно, |
||
найдется такое значение номера члена последовательности |
N (например, |
N 500), что |
|
все последующие члены отличаются от a меньше чем и на это . И.т.д. |
|
|
|
Если последовательность имеет предел a, то говорят, что она сходится (к |
a). В |
||
противном случае, говорят, что последовательность расходится. Для обозначения сходимости последовательности к числу a используется также формы записи
n
xn a, при n , или xn a.
Примеры.
1. lim 1 0. Действительно, рассматриваемая последовательность имеет вид
n n
1,1,1,1,.... Очевидно, что члены последовательности с достаточно большими номерами
2 3 4
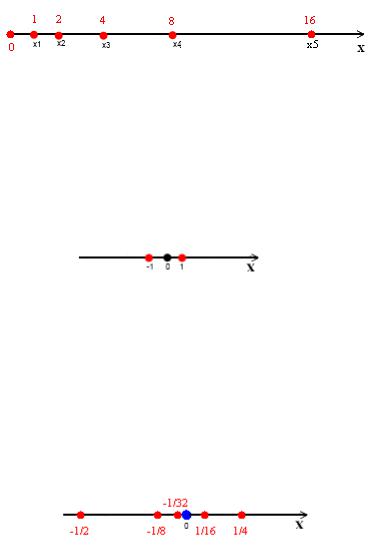
будут сколь угодно близки к нулю (рис. 3).
Рис. 3. Иллюстрация сходимости последовательности xn 1/n .
1
Более строго. Для любого, сколь угодно малого числа 0, при n N (напомню,
что квадратные скобки означают целую часть числа, например, [2.5] 2) выполняется
неравенство | xn | . Это и означает, что limxn 0. В таблице 1 приведены значения N
n
для трех различных значений .
Таблица 1.
|
0.1 |
|
0.01 |
|
0.001 |
N |
10 |
|
100 |
|
1000 |
Видим, что члены последовательности с номерами |
n 10 |
отличаются от предела a 0 |
|||
меньше чем на 0.1, члены последовательности с n 100 – меньше чем на 0.01 и т.д. Сколь
13
бы малым мы не задали 0, члены последовательности с достаточно большими номерами (большими некоторого номера N( )) будут отличаться от значения предела a 0 меньше чем на .
1 |
|
|
|
|
|
|
|
|
|
1 |
|
||
2. lim10 |
n |
1. |
Действительно, поскольку члены |
последовательности |
x |
при |
|||||||
n |
|||||||||||||
n |
|
|
n будут сколь угодно близки |
|
нулю, а 100 1, |
n |
|
||||||
достаточно больших |
|
к |
то |
члены |
|||||||||
|
|
|
x |
|
1 |
|
n |
|
|
|
|
||
последовательности |
n |
10 |
n |
при достаточно больших |
будут сколь угодно близки к |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
a 1 (позже будет доказана теорема о пределе сложной функции, придающая строгий смысл этим рассуждениям).
3. Последовательность xn 2n расходится. Действительно, эта последовательность имеет вид 2,4,8,16,32,.... Очевидно, что не существует такого числа a, что все члены последовательности с достаточно большими n сколь угодно близки к a (рис. 4).
Отметим, что для данной последовательности характерна следующая черта. Члены с достаточно большими n сколь угодно велики (при достаточно больших n члены последовательности будут больше любого, сколь угодно большого, наперед заданного числа ). В таких случаях говорят, что предел
последовательности равен плюс бесконечности: lim2n (частный случай расходимости
n
последовательности).
Рис. 4. Иллюстрация расходимости последовательности xn 2n .
4. Последовательность xn ( 1)n тоже расходится. Она имеет вид: 1,1, 1,1, 1,1,....
Члены последовательности «прыгают» то вправо, то влево от нуля, повторяя одну и ту же пару значений (рис. 5), и ни к какому a последовательность не сходится (не существует такого числа a, что все члены последовательности с достаточно большими n сколь угодно мало отличаются от a).
Рис.5.Последовательностьxn ( 1)n .
5. Нетрудно видеть, что lim( 1)n 2 n 0 (рис. 6). Члены последовательности имеют
|
|
|
|
|
|
|
|
|
|
n |
вид |
1 |
, |
1 |
, |
1 |
, |
1 |
, |
1 |
,.... Этот пример подобен примеру, представленному на рис. 1 (в |
|
|
|
|
|
||||||
2 |
4 |
8 |
16 |
32 |
|
|||||
случае a 0), но при этом члены последовательности «прыгают» то вправо, то влево относительно предела a 0. Пример подчеркивает существенность модуля в неравенстве | xn a| , фигурирующем в определении предела.
Рис. 6. Иллюстрация сходимости последовательности xn ( 1)n 2 n .
14

6. Покажем, что lim |
3n 1 |
|
3 |
. Будем отталкиваться от определения предела. |
|
|
|||
n 2n 4 |
2 |
|
||
Выберем любое, сколь угодно малое 0 и запишем неравенство | xn a| для данного случая:
3n 1 |
|
3 |
|
. |
(1) |
|
|
||||
2n 4 2 |
|
|
|
||
После приведения дробей под знаком модуля к общему знаменателю, получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|2n 4| |
|
|
|
|
|
|
|
|
|
|||||||||
откуда |2n 4| |
7 |
. |
Раскрывая |
модуль, видим, |
что |
при |
n |
7 |
2 действительно |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
выполняется неравенство (1). Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
N |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
|
(2) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда при n N справедливо неравенство (1). Таким образом, |
|
||||||||||||||||||||||||||||||
|
|
|
|
7 |
|
|
|
|
|
|
3n 1 |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
0 N |
|
|
|
2 : n N |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
2n 4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Последнее и означает, что lim |
3n 1 |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n 2n 4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Интересно исследовать зависимость N( ) |
на данном примере. Она выражается формулой |
||||||||||||||||||||||||||||||
(2). В таблице 2 приведены значения N для трех различных значений . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
0.01 |
|
|
|
0.001 |
|||||||||
N |
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
348 |
|
|
|
3498 |
|||||||||
|
§2. Основные свойства предела последовательности |
||||||||||||||||||||||||||||||
Теорема. |
|
Пусть |
xn c, n 1,2,3,..., |
|
|
|
|
|
где |
с – постоянная (т.е. члены |
|||||||||||||||||||||
последовательности не зависят от n. Тогда limx |
n |
c. |
|
|
|
|
|
|
|||||||||||||||||||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||
Зададим |
произвольное |
0 |
и |
выберем |
произвольное N |
||||||||||||||||||||||||||
(например, N 1) . |
Очевидно, |
что |
при |
n N |
|
| xn |
c| |c c| 0 , |
что и означает (в |
|||||||||||||||||||||||
соответствии с определением предела), что limxn c.
n
Теорема доказана.
Теорема. (О единственности предела). Если предел последовательности {xn}
существует, то он единственен.
Доказательство. Доказательство проведем от противного. Предположим, что существует два различных предела последовательности {xn}:
lim xn a и limxn b, причем a b.
n n
Пусть, для определенности, b>a. Выберем
b a 0. 2
15

Тогда по определению предела
N1 : n N1 | xn a|N2 : n N2 | xn b|
Обозначим через N наибольшее среди чисел N1 и N2 : N max{N1,N2}, тогда при n N
выполняются оба неравенства:
|
|
|
x a |
b a |
|
x |
|
a b |
|
|
||||
|
|
|
|
|
|
|
||||||||
| x |
|
a| |
|
|
n |
|
|
|
|
n |
|
|
|
|
n |
|
|
|
2 |
|
|
|
2 . |
||||||
|
|
|
|
|
|
|
|
|||||||
| xn b| |
x b |
b a |
x |
a b |
|
|||||||||
|
|
|||||||||||||
|
|
|
|
n |
|
2 |
|
|
n |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
Приходим к противоречию. Следовательно, наше предположение о существовании двух различных пределов было неверным и предел единственен.
Теорема доказана.
Теорема (необходимое условие сходимости последовательности). Всякая сходящаяся последовательность ограничена.
Доказательство. Итак, пусть последовательность {xn} сходится и ее предел равен
a: lim xn a . Зададим произвольное 0. По определению предела,
n
N 0: n N | xn a| => xn a => a xn a .
С другой стороны при n N имеется конечное множество элементов 
 . Наибольший из них обозначим M1 , а наименьший – m1 . Обозначим, далее, через M наибольшее из чисел
. Наибольший из них обозначим M1 , а наименьший – m1 . Обозначим, далее, через M наибольшее из чисел
M1 и a , а через m – наименьшее из чисел m1 и a :
M max{M1,a }, m min{m1,a }.
Имеем n: m xn M , т.е. последовательность {
 } ограничена и сверху и снизу, а
} ограничена и сверху и снизу, а
значит ограничена.
Теорема доказана.
Без доказательства сформулируем последнее из рассматриваемых здесь свойств предела последовательности.
Теорема (теорема Вейерштрасса или достаточное условие сходимости последовательности). Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится, причем ее предел равен ее точной верхней грани.
|
|
1 |
n |
||
§3. Предел последовательности xn |
1 |
|
|
. Гиперболические функции. |
|
n |
|||||
|
|
|
|
||
|
1 |
n |
||
Теорема. Существует предел последовательности a lim 1 |
|
|
, причем этот |
|
n |
||||
n |
|
|
||
предел удовлетворяет неравенству 2 a 3.
16
Рассматриваемый предел называется числом Эйлера или числом e:
|
1 n |
|
e lim 1 |
|
. |
|
||
n |
n |
|
Вычисление значения данного предела с точностью до третьего знака после запятой дает: e 2.718. Число e играет важную роль в математическом анализе и фигурирует во многих формулах и задачах. Показательная функция y ex с основанием e называется экспонентой, а логарифмическая функция по снованию e – натуральным логарифмом: y loge x ln x . Обычно, если речь идет о натуральном логарифме, слово «натуральный»
пропускается, т.е., если не указано основание логарифма, подразумевается, что логарифм натуральный. Экспонента и натуральный логарифм – взаимнообратные функции, т.е.
y ex x ln y .
Введем понятие гиперболических функций. Гиперболический синус определяется равенством:
shx ex e x . 2
Гиперболический косинус:
chx ex e x . 2
Гиперболический тангенс:
thx shx . chx
Гиперболический котангенс:
cthx chx . shx
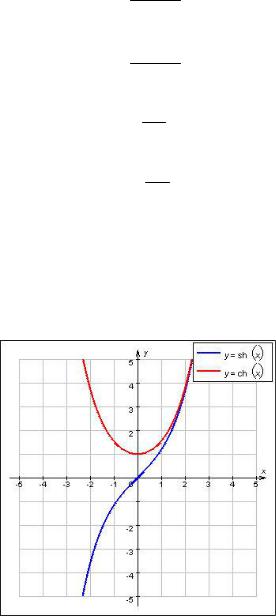
Нетрудно видеть, что shx - нечетная функция, аchx - четная. На рис. 7 представлены графики гиперболического синуса и гиперболический косинуса.
Выпишем без доказательства некоторые основные соотношения между гиперболическими функциями (их легко получить из определений этих функций):
ch2x sh2x 1 sh2x 2shx chx ch(2x) ch2x sh2x.
Рис. 7. Графики функций y shx и y chx.
17
Лекция 3
§1. Предел действительной функции одного действительного переменного (R R ).
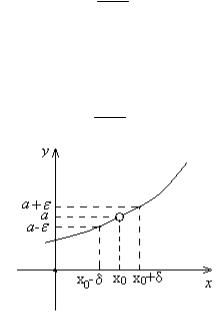
Говорят, что предел функции f (x) при x стремящемся к x0 равен a, если в достаточно малой окрестности точки x0 значения функции f (x) сколь угодно близки к числу a. Более строго определение предела формулируется следующим образом.
Опр. Число a называется пределом функции f (x) при x стремящемся к x0 , если для любого сколь угодно малого положительного числа существует такое достаточно
малое положительное число , |
что |
в |
проколотой |
окрестности |
|
|
|
точки |
x0 |
||||
u (x0 ) |
|
||||||||||||
выполняется неравенство | |
f (x) a| : |
|
|
|
|
|
|
|
|
||||
|
|
x x0 |
|
df |
|
|
|
0 |
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
a lim |
f (x) |
|
0 |
0: x u |
(x ) | f (x) a| |
|
|
|
|||
Число x0 |
называется предельной точкой. |
Отметим, что условие x |
|
|
|
очевидно, |
|||||||
u (x0), |
|||||||||||||
эквивалентно неравенству 0 | x x0 |
| . |
|
|
|
|
|
|
|
x |
||||
Геометрический смысл этого определения иллюстрируется рис. 1: если |
значения |
||||||||||||
попадают |
в интервал (x0 ,x0 ) |
|
или |
(x0,x0 ), то |
соответствующие |
значения |
y |
||||||
попадают в интервал (a ,a ). |
|
|
|
|
|
|
|
|
|
|
|||
Если элементарная функция |
|
f (x) |
определена в точке x0 , то ее предел при x x0 |
|
|||||||||
часто равен ее значению в этой точке (в этом случае функция называется непрерывной): |
|
||||||||||||
lim f (x) f (x0). |
|
|
|
|
|
|
|
|
|
|
|
||
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
limsin x 0, limcosx 1 и т.д. |
|
|
|
|
|
|
|
|
|||||
x 0 |
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
Однако, в общем случае, функция может быть не определена в точке x0 , но при этом иметь предел при x x0 . Чтобы подчеркнуть это, на рис. 1 точка (x0,a) изображена в виде пустого кружочка.
Пример. Рассмотрим функцию y sin x . Как известно, она не определена в точке x
x 0. Тем не менее, если вычислять значения этой функции в точках все более и более близких к нулю, можно убедиться, что эти значения все более и более близки к единице. Более того, значения этой функции будут сколь угодно мало отличаться от единицы при x достаточно близких к нулю. По определению, это означает, что
limsin x 1.
x 0 x
Рис. 1. Геометрический смысл определения предела.
18

Позже это равенство будет доказано аналитически, на основе определения предела (этот предел называется первым замечательным пределом).
Пример. Функция y x2 x 2 не определена при x 1. Вычислим предел этой функции при x 1.
lim x |
2 |
x 2 |
|
0 |
|
(x 1)(x 2) |
lim x 2 |
3 . |
||||
lim |
||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
x 1 |
|
x2 1 |
|
|
x 1 |
(x 1)(x 1) |
x 1 |
2 |
|
|||
Символ «0 » над знаком «равно» означает, что при подстановке в дробь под знаком
0
предела значения x 1, и числитель и знаменатель этой дроби принимают нулевое значение. Из-за этого предел не может быть вычислен непосредственно подстановкой
предельного значения аргумента, как в случае предела limsin x 0. В подобных случаях,
x 0
говорят о наличии неопределенности. В рассмотренном пределе имеет место
неопределенность « |
0 |
». В дальнейшем |
мы |
столкнемся |
с |
другими |
типами |
||||
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
неопределенностей. Известны следующие основные типы: |
|
|
|
||||||||
|
|
|
0 |
, |
|
,0 , ,1 ,00, 0 . |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|||
Опр. Число a называется пределом функции |
f (x)при x стремящемся к x0 |
справа |
|||||||||
(правосторонним пределом функции f (x)при |
x стремящемся к |
x0 ), |
если для любого |
||||||||
сколь угодно |
|
малого |
положительного числа |
существует |
такое достаточно малое |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
точки x0 |
положительное число , что в правосторонней проколотой окрестности u (x0 |
|||||||||||||||
выполняется неравенство | f (x) a| : |
|
|
|
|
|
|
|
|
|
||||||
|
|
x x0 |
|
df |
|
|
|
|
0 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a lim |
f (x) |
|
0 0: x |
u |
(x ) | f (x) a| |
|
|
|
||||||
|
|
(x0 ) |
эквивалентно |
неравенству |
x0 x x0 . |
Геометрический смысл |
|||||||||
Условие x u |
|||||||||||||||
этого определения иллюстрируется |
рис. |
2: если значения |
x |
попадают |
в |
интервал |
|||||||||
(x0,x0 ), то соответствующие значения y |
попадают в интервал (a,a ). |
|
|
|
|||||||||||
Рис. 2. Геометрический смысл определения предела функции при x x0 .
Аналогично определяется предел функции при x стремящемся к x0 слева.
19
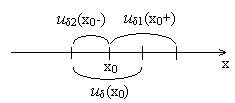
Пример. Рассмотрим функцию y xln x . Она |
определена только при x 0. |
Поэтому не имеет смысла говорить о ее пределе при x |
стремящемся к x0 . Тем не менее, |
если вычислять значения этой функции для положительных x, все более и более близких к нулю, то значения y будут также все более и более близки к нулю. Более того, y будет сколь угодно мало отличаться от нуля, если только x достаточно близко к нулю, т.е. доказать, что
lim xln x 0.
x 0
Позже это равенство будет доказано аналитически.
Пределы функции при x x0 и при x x0 будем называть односторонними
пределами, а предел при x x0 – двусторонним. Справедлива следующая теорема.
Теорема (о связи двустороннего предела функции с односторонними). Двусторонний предел функции при x x0 существует тогда и только тогда, когда
существуют оба соответствующих односторонних предела и они равны. При этом двусторонний предел равен односторонним.
Доказательство. Докажем эту теорему в два этапа. Сначала прямое утверждение, затем обратное.
1. Пусть существуют оба односторонних предела функции f (x) и они равны a. Покажем, что в этом случае существует также двусторонний предел функции и он тоже равен a. Зададим произвольное сколь угодно малое 0. Т.к.
lim |
f (x) a, |
для этого существует такое |
1 0, что |
|
(x0 ) |
выполняется |
||||
при x u |
||||||||||
x x0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
неравенство | |
f (x) a| . Т.к. lim |
f (x) a, |
для этого |
существует такое 2 0, что |
||||||
|
|
|
|
|
x x0 |
|
|
|
|
|
при |
|
(x0 |
) |
выполняется неравенство | f (x) a| . Обозначим через |
наименьшее |
|||||
x u 2 |
||||||||||
из чисел 1 |
и |
2 . Очевидно (рис. |
3), что неравенство | f (x) a| |
выполняется при |
||||||
|
|
Последнее и означает, что существует lim f (x) a . |
|
|
||||||
x u (x0). |
|
|
||||||||
|
|
|
|
|
|
|
x x0 |
|
|
|
2. Пусть существует двусторонний предел функции f (x) и он равен a. Покажем, что в этом случае существуют оба односторонних предела этой функции и они тоже равны a.
Зададим произвольное сколь угодно малое 0. Т.к. lim f (x) a , для этого
|
|
x x0 |
|
|
(x0) |
выполняется неравенство | f (x) a| . Но, |
|
существует такое 0, что при x u |
|||
|
|
|
|
следовательно, оно выполняется при x u |
(x0 ), так и при x u (x0 ). Первое означает, |
||
что существует lim f (x) a, а второе, что существует lim |
f (x) a. |
||
x x0 |
|
x x0 |
|
Теорема доказана.
20
