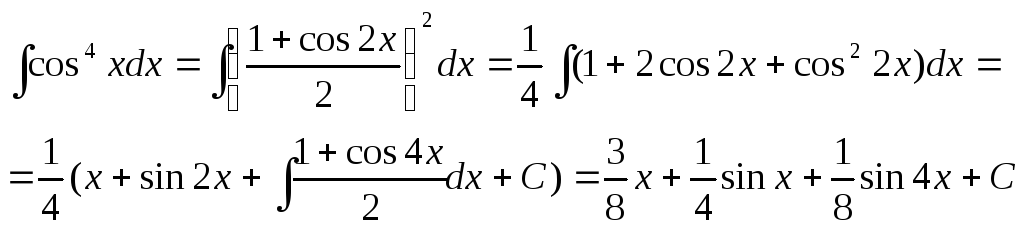Интегрирование некоторых иррациональных выражений.
Интегрирование иррациональных выражений, вообще говоря, представляет большую трудность. Многие интегралы от иррациональных функций не выражаются через элементарные функции. Поэтому мы рассмотрим только некоторые частные случаи, когда заменой переменных можно от интеграла от иррациональной функции перейти к интегрированию рациональных выражений.
1.Рассмотрим интеграл вида
где R– рациональная функция,m, n, … p,q– целые числа
Пусть к- общий знаменатель дробей
.
Применим
подстановку
Тогда каждая дробная степень выразится через целую степень tи иррациональная функция преобразуется в рациональную
Например
Применим
подстановку
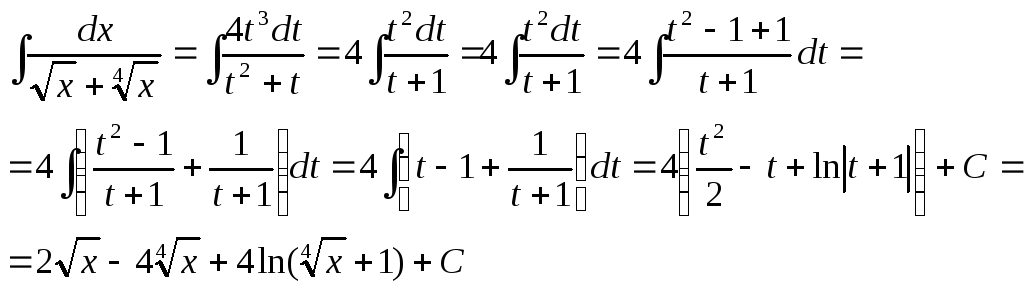
2.Интегралы вида
вычисляются с помощью подстановки
гдеk- наименьшее общее кратное чиселn…q
Эта подстановка сведет интеграл от иррациональной функции к интегралу от рациональной дроби.
Например:
Обозначим
тогда
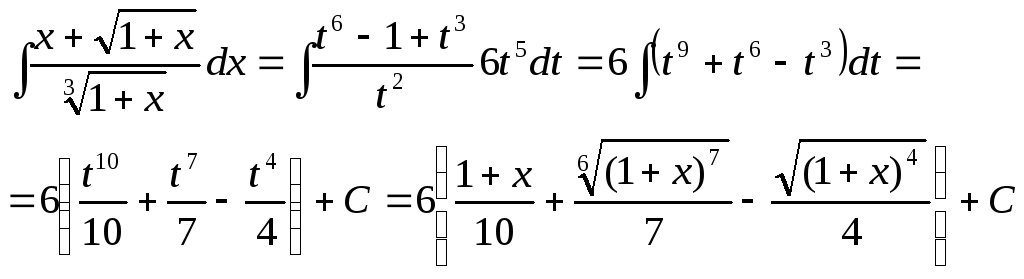
Интегрирование тригонометрических функций
Пусть требуется
найти
интеграл вида
Применим
подстановку
тогда
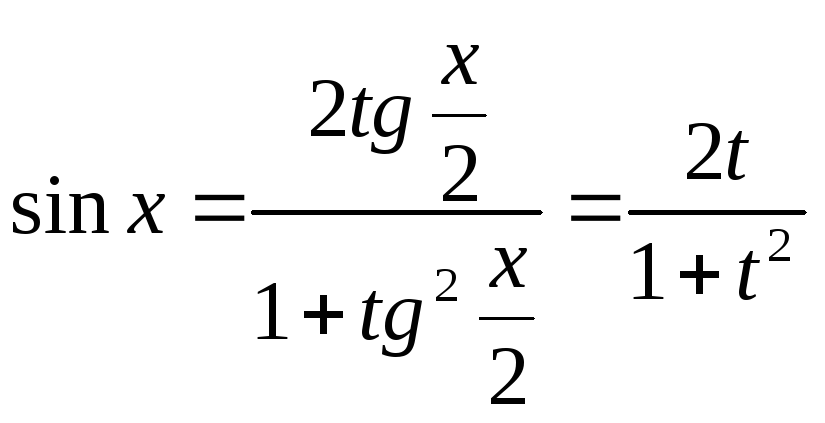
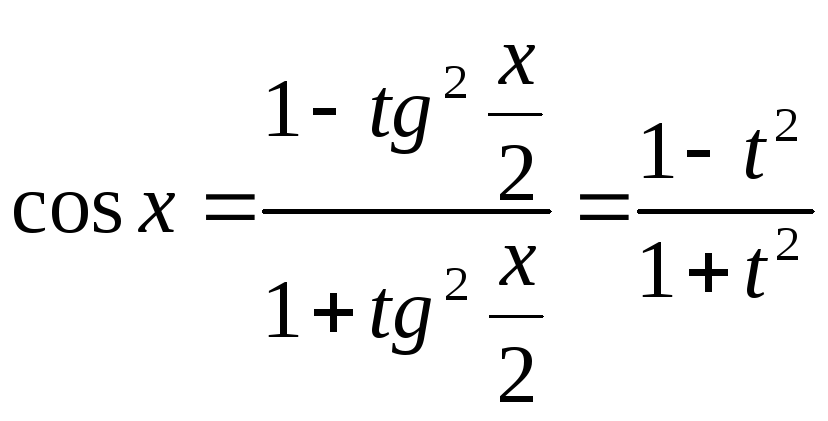
Далее найдем
Подстановка
,
носит названиеуниверсальной
тригонометрическойподстановки;
она сводит вычисление интеграла от
тригонометрических функций к интегрированию
рациональных выражений.
Например:
Обозначим 
тогда
Тогда
Интегралы от степеней тригонометрических функций
Рассмотрим интегралы вида
, гдеmиn–действительные числа
а) Пусть mиn – действительные числа и по крайней мере одно из них положительное, нечетное, например,n=2p+1. В этом случае интегрирование проводят следующим способом:
Обозначим sin x = t
Таким образом, вычисление интеграла свелось к интегрированию рациональной функции.
Пример 1:
обозначим sin x = t
Пример 2:
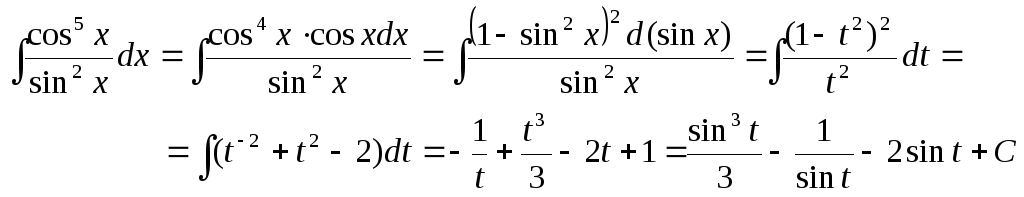
Обозначим sin x = t
б) Пусть mиnдействительные положительные четные числа (m=2p, n=2q). Интегрирование тригонометрических функций в этом случае может быть сведено к интегрированию рациональных функций посредством известных из тригонометрии формул:
Заменим в подынтегральном выражении четные степени синуса и косинуса по указанным формулам.
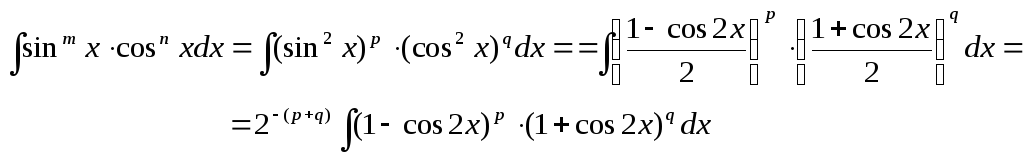
Далее возведем двучлены в указанные степени, получим вновь четные и нечетные степени синуса и косинуса. Нечетные степени проинтегрируем как указано в пункте а), четные степени снова понизим по формулам понижения четных степеней.
Например:
