- •Неопределенный интеграл.
- •Свойства неопределенного интеграла.
- •Непосредственное интегрирование.
- •Интегрирование методом подстановки.
- •Метод подведения под знак дифференциала.
- •Интегрирование по частям.
- •Интегрирование рациональных функций
- •Интегрирование некоторых иррациональных выражений.
- •Интегрирование тригонометрических функций
- •Интегралы от степеней тригонометрических функций
Неопределенный интеграл.
Основной задачей дифференциального исчисления является нахождение производной или дифференциала от данной функции.
В интегральном
исчислении основной задачей является
обратная задача – отыскание функции
![]() по заданной ее производной
по заданной ее производной![]() или дифференциалу
или дифференциалу![]() ,
т.е. для данной функции
,
т.е. для данной функции![]() надо найти такую функцию
надо найти такую функцию![]() ,
что:
,
что:
![]() или
или
![]()
Функция
![]() называетсяпервообразной для
функции
называетсяпервообразной для
функции![]() на отрезке [a,b],
если во всех точках этого отрезка
выполняются равенства
на отрезке [a,b],
если во всех точках этого отрезка
выполняются равенства
![]() или
или
![]()
Например, для
функции
![]() первообразной будет функция
первообразной будет функция
![]() т.к.
т.к.![]()
Легко видеть,
что если
![]() первообразная для функции
первообразная для функции![]() ,
то функция
,
то функция![]() тоже является первообразной для функции
тоже является первообразной для функции![]() ,
так как
,
так как
![]()
Если
функция
![]() является первообразной для функции
является первообразной для функции![]() ,
то выражение называетсянеопределенным
интеграломот функции
,
то выражение называетсянеопределенным
интеграломот функции![]() и обозначается символом
и обозначается символом
![]()
Функция
![]() называется подынтегральной функцией,
называется подынтегральной функцией,![]() – подынтегральным выражением, С –
произвольная постоянная.
– подынтегральным выражением, С –
произвольная постоянная.
Нахождение первообразной для данной функции называется интегрированием.
Свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции
![]()
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
![]()
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.
![]()
Справедливость свойств 1 – 3 вытекает непосредственно из определения неопределенного интеграла.
4.Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов
![]()
Для доказательства достаточно найти производные от левой и правой частей этого равенства
![]()
![]()
![]()
![]()
5. Постоянный множитель можно выносить за знак интеграла
![]()
Для доказательства найдем производные от левой и правой частей равенства
![]()
![]()
6. Если функция
![]() является первообразной для функции
является первообразной для функции![]() ,
то функция
,
то функция
![]() является первообразной для функции
является первообразной для функции![]() ,
то есть, если
,
то есть, если![]() ,
то
,
то![]()
Для доказательства найдем производные от левой и правой частей равенства
![]()
Таблица интегралов.
![]() Таблица интегралов получается
непосредственно из определения
неопределенного интеграла и таблицы
производных. Для установления
справедливости указанных в таблице
формул достаточно найти производные
от правых частей равенств и получить
подынтегральные функции.
Таблица интегралов получается
непосредственно из определения
неопределенного интеграла и таблицы
производных. Для установления
справедливости указанных в таблице
формул достаточно найти производные
от правых частей равенств и получить
подынтегральные функции.
Заметим, что функций, стоящих в правых частях последних формул нет в таблице производных. Однако, эти интегралы часто встречаются в практических задачах, поэтому они помещены в таблицу. Справедливость их нетрудно проверить непосредственным дифференцированием функций, стоящих в правых частях равенств.
Например, формула 12 доказывается так:
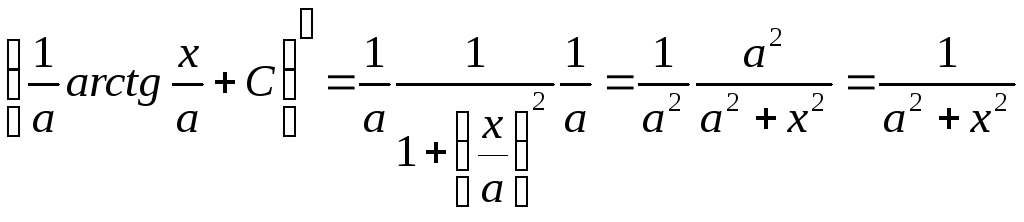
Аналогично проверяются остальные формулы.
Непосредственное интегрирование.
Пользуясь таблицей интегралов, свойствами неопределенного интеграла и различными алгебраическими или трансцендентными преобразованиями подынтегральных функций можно вычислить многие интегралы.
Например:
Интегрирование методом подстановки.
Пусть
требуется найти интеграл
![]() непосредственное интегрирование,
которого не дало окончательного
результата.
непосредственное интегрирование,
которого не дало окончательного
результата.
Заменим
переменную в подынтегральном выражении,
положив
![]() ,
где
,
где![]() непрерывная вместе со своей производной
функция. Получим
непрерывная вместе со своей производной
функция. Получим
![]() .
.
Вычислим
полученный интеграл по переменной
![]() ,
а затем после интегрирования по переменной
,
а затем после интегрирования по переменной![]() перейдем к прежней переменной
перейдем к прежней переменной![]() ,
вновь воспользовавшись формулой
,
вновь воспользовавшись формулой![]()
Например:
1.
![]()
Сделаем замену
переменной, положив
![]() ,
тогда интеграл примет вид
,
тогда интеграл примет вид
![]()
2.
![]()
Положим
![]() ,
отсюда выразим
,
отсюда выразим![]() и найдем
и найдем![]()
Тогда
![]()
3.
![]()
Полагаем
![]() ,
тогда
,
тогда![]()
![]()
4.
![]()
Положим
![]() тогда
тогда
![]()
Заметим, что подобрать нужную подстановку удается не всегда быстро, необходимы определенные навыки и практический опыт.