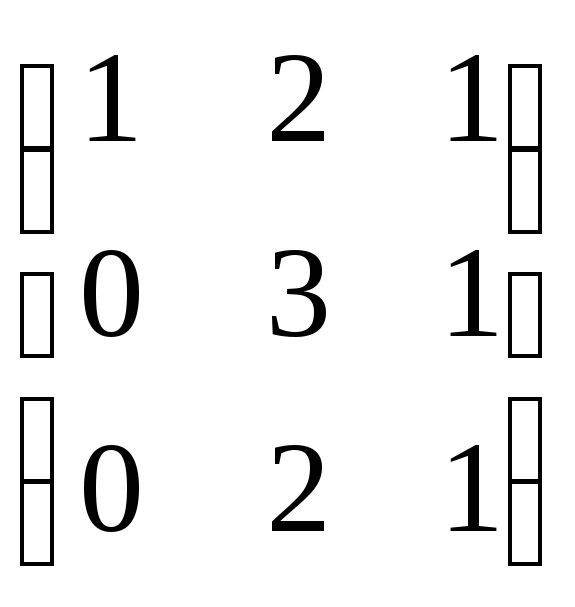
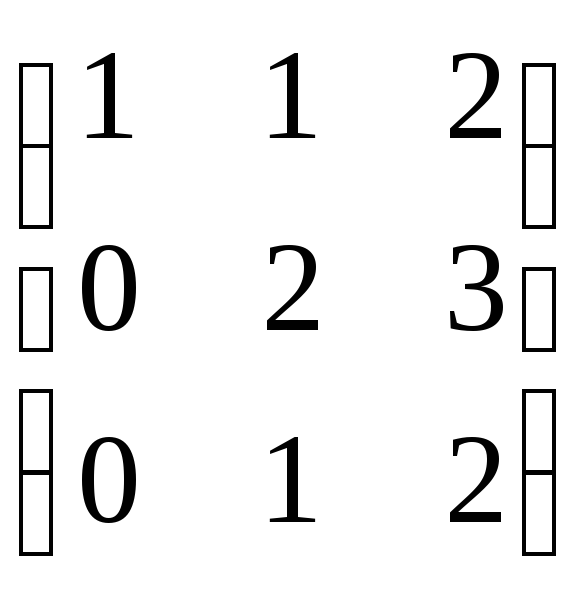
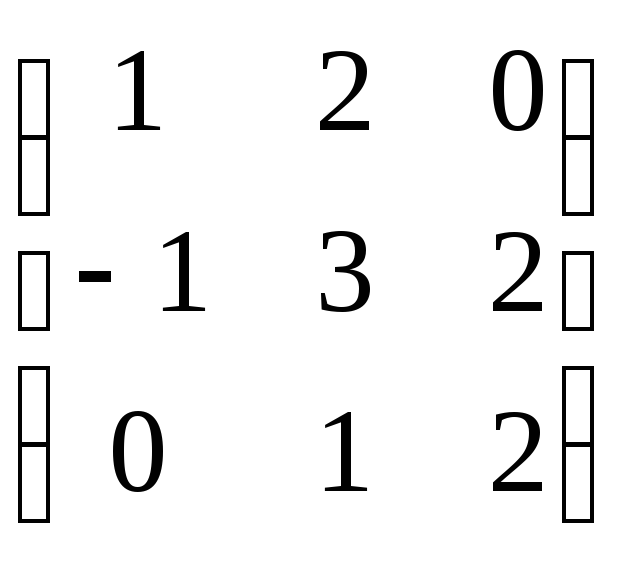
Решение матричных уравнений
.docКалужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Московский государственный технический университет имени Н.Э. Баумана»
(КФ МГТУ им. Н.Э. Баумана)
Влайков Н.Д.
Решение матричных уравнений
Методические указания для проведения упражнений
по курсу аналитической геометрии
Калуга 2011г.
Содержание.
Цели занятия стр.4
План занятия стр.4
Необходимые теоретические сведения стр.5
Практическая часть стр.6
Контроль освоения пройденного материала стр.10
Домашнее задание стр.11
Количество часов: 2
Цели занятия:
-
Систематизировать полученные теоретические знания о видах матричных уравнений и способах их решения.
-
Применить на практике методы решения матричных уравнений.
План занятия:
-
Кратко изложить теоретический материал.
-
Решить матричное уравнение вида
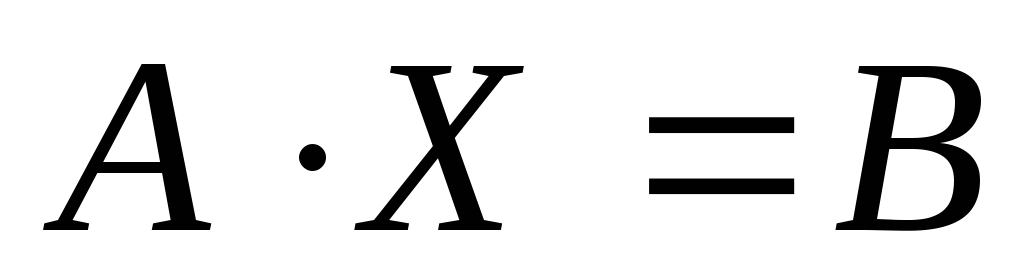 методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы. -
Решить матричное уравнение вида
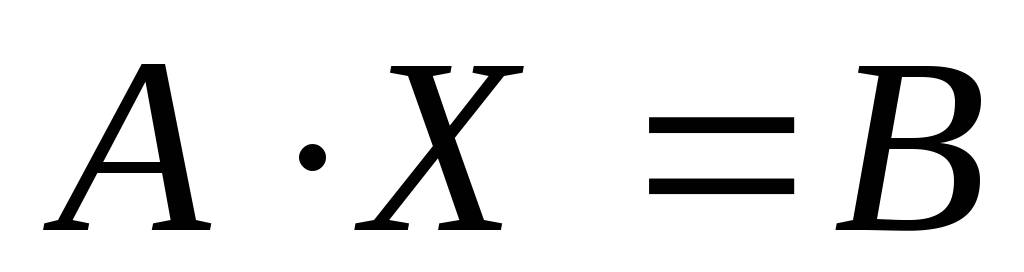 методом,
основанным на элементарных преобразованиях
строк матрицы.
методом,
основанным на элементарных преобразованиях
строк матрицы. -
Сравнить использованные методы.
-
Решить матричное уравнение вида
 методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы. -
Решить матричное уравнение вида
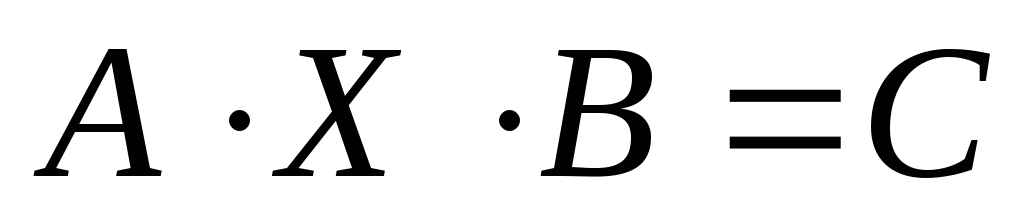 методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы. -
Проверить выполнение текущего домашнего задания.
-
Провести проверочную работу.
-
Представить тему следующего семинарского занятия.
-
Выдать текущее домашнее задание.
Необходимые теоретические сведения.
Рассмотрим
два вида матричных уравнений относительно
неизвестной матрицы
![]() :
:
![]() и
и
![]() ,
где матрицы
,
где матрицы
![]() и
и
![]() - известны, причем
- известны, причем
![]() - квадратная и невырожденная.
- квадратная и невырожденная.
Опр.
Некоторую матрицу называют решением
матричного уравнения относительно
неизвестной матрицы
![]() ,
если при ее подстановке вместо
,
если при ее подстановке вместо
![]() матричное уравнение превращается в
тождество.
матричное уравнение превращается в
тождество.
Рассмотрим
уравнение
![]() .
.
Первый
метод предполагает
вычисление обратной матрицы
![]() и дает запись решения матричного
уравнения в виде
и дает запись решения матричного
уравнения в виде
![]() .
Причем данное решение единственно.
.
Причем данное решение единственно.
Второй
метод
основан на элементарных преобразованиях
строк блочной матрицы
![]() и имеет своей целью преобразование ее
к виду
и имеет своей целью преобразование ее
к виду
![]() ,
в котором вместо матрицы
,
в котором вместо матрицы
![]() стоит единичная матрица
стоит единичная матрица
![]() .
Тогда матрица
.
Тогда матрица
![]() и будет решением уравнения.
и будет решением уравнения.
Проверка ответа выполняется подстановкой найденного решения в исходное уравнение.
Матричное
уравнение
![]() так же можно решить двумя способами.
Если известна матрица
так же можно решить двумя способами.
Если известна матрица
![]() ,
то умножаем справа на
,
то умножаем справа на
![]() матричное уравнение
матричное уравнение
![]() и после очевидных преобразований
получаем ответ в виде произведения двух
матриц
и после очевидных преобразований
получаем ответ в виде произведения двух
матриц
![]() .
Другой метод решения матричного уравнения
.
Другой метод решения матричного уравнения
![]() состоит
в транспонировании его левой и правой
частей
состоит
в транспонировании его левой и правой
частей
![]() ,
,
![]() .
После введения новой неизвестной матрицы
.
После введения новой неизвестной матрицы
![]() получаем уравнение вида
получаем уравнение вида
![]() ,
которое решается методом элементарных
преобразований.
,
которое решается методом элементарных
преобразований.
Практическая часть.
Пример
1. Решить
матричное уравнение:
![]() ,
,
где
![]() ;
;
![]() .
.
Решение.
1-ый способ. Найдем решение, используя обратную матрицу:
Решение
ищем в виде
![]() ;
;
Найдем
матрицу
![]() (например, при помощи присоединенной
матрицы)
(например, при помощи присоединенной
матрицы)
![]() .
.
Таким образом, получим:
![]() .
.
2-ой способ. Найдем решение методом элементарных преобразований:
Запишем
матрицу
![]() и выполним элементарные преобразования
ее строк с целью привести ее к виду
и выполним элементарные преобразования
ее строк с целью привести ее к виду
![]() .
.
![]()
![]() .
.
Следовательно,
![]() .
.
Проверка осуществляется подстановкой в исходное уравнение:
![]() -
Верно.
-
Верно.
Пример
2. Решить
матричное уравнение:
![]() ,
,
где
![]() ;
;
![]() ;
;
![]() .
.
Решение.
Если
для матриц
![]() и
и
![]() существуют обратные матрицы
существуют обратные матрицы![]() и
и
![]() соответственно, умножим обе части
уравнения слева на
соответственно, умножим обе части
уравнения слева на
![]() ,
справа на
,
справа на
![]() .
В результате получим:
.
В результате получим:
![]() .
Учитывая, что
.
Учитывая, что
![]() ,
,
![]()
(![]() -
единичная матрица) можно записать:
-
единичная матрица) можно записать:
![]() .
Так как
.
Так как
![]() -
единичная матрица, окончательно имеем
уравнение:
-
единичная матрица, окончательно имеем
уравнение:
![]()
где
матрица
![]() - решение уравнения.
- решение уравнения.
Если
же хотя бы одна из матриц
![]() или
или
![]() не имеет обратную, уравнение не имеет
решения.
не имеет обратную, уравнение не имеет
решения.
Для
матрицы
![]() найдем
найдем
![]() или
докажем, что она не существует.
или
докажем, что она не существует.
а)
![]() обратная
матрица существует.
обратная
матрица существует.
б)
![]() .
.
в)
Найдем алгебраические дополнения для
матрицы
![]() и
составим из них присоединенную матрицу
и
составим из них присоединенную матрицу
![]() :
:
![]() .
.
г)
Известно, что
![]() ;
тогда
;
тогда
![]() .
.
Для
матрицы
![]() найдем
найдем
![]() или докажем, что она не существует.
или докажем, что она не существует.
а)
![]() обратная
матрица существует.
обратная
матрица существует.
б)
![]() .
.
в)
Найдем алгебраические дополнения для
матрицы
![]() и
составим из них присоединенную матрицу
и
составим из них присоединенную матрицу
![]() :
:
![]() .
.
г)
По формуле
![]() ;
;
![]() .
.
Найдем
неизвестную матрицу
![]() .
.
![]()
![]()
![]() .
.
Ответ:![]() .
.
Решить матричные уравнения:
№2.121(2.39)
![]() .
Отв.:
.
Отв.:
![]()
№2.122(2.40)
![]() .
Отв.:
.
Отв.:
![]()
№2.123(2.41)
![]() .
Отв.:
.
Отв.:
![]()
№2.124(2.42)
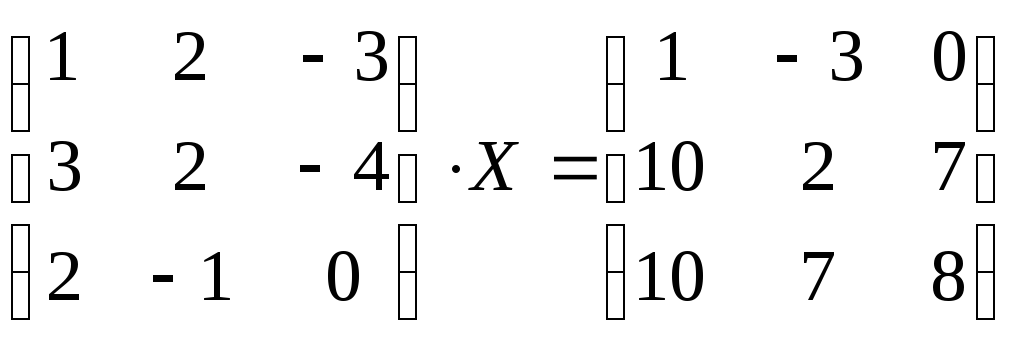 .
Отв.:
.
Отв.:
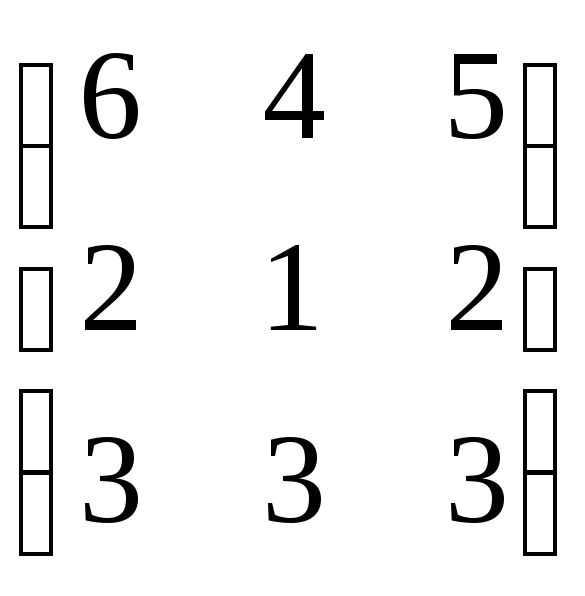
№2.125(2.43)
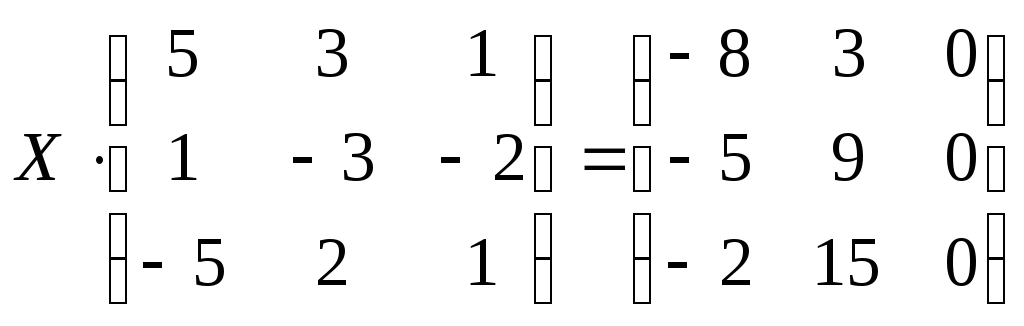 .
Отв.:
.
Отв.:
Представление темы следующего семинара.
Решение систем линейных однородных уравнений.
Контроль освоения пройденного материала.
Проверочная работа 5 минут. Участвует 4 студента с четными номерами по журналу, начиная с №10
Задание:
|
Вар№1 Выполнить действия:
|
Вар№2 Выполнить действия:
|
|
Вар№3 Найти матрицу обратную данной:
|
Вар№4 Найти матрицу обратную данной:
|
Ответы:
|
Вар№1 Выполнить действия:
|
Вар№2 Выполнить действия:
|
|
Вар№3 Найти матрицу обратную данной:
|
Вар№4 Найти матрицу обратную данной:
|
Домашнее задание.
1.Решить
матричное уравнение
![]() :
:
1)
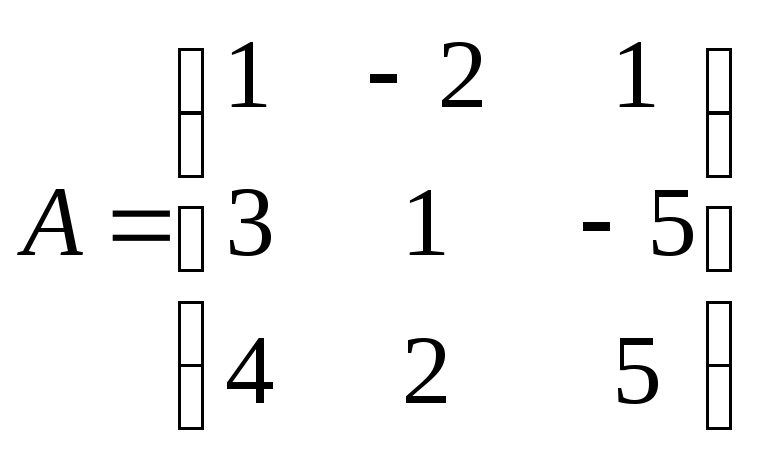 ;
;
 .
.
2)
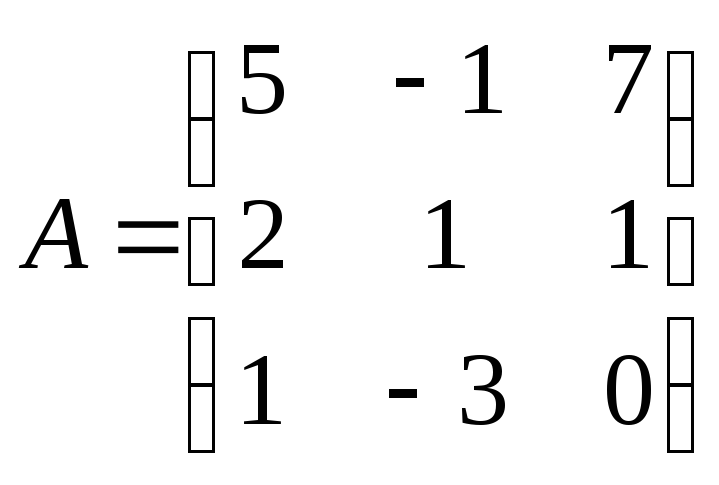 ;
;
 .
.
2.Решить
матричное уравнение
![]() :
:
1)
![]() ;
;
![]() ;
;
![]() .
.
2)
![]() ;
;
![]() ;
;
![]() .
.
3.Проработка лекций на темы:
Системы линейных алгебраических уравнений (СЛАУ). Координатная, матричная и векторная формы записи. Критерий Кронекера — Капелли совместности СЛАУ. Однородные СЛАУ. Критерий существования ненулевого решения однородной СЛАУ. Свойства решений однородной СЛАУ. Фундаментальная система решений однородной СЛАУ, теорема о ее существовании. Нормальная фундаментальная система решений. Теорема о структуре общего решения однородной СЛАУ.