Решение однородных СЛАУ
.docКалужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Московский государственный технический университет имени Н.Э. Баумана»
(КФ МГТУ им. Н.Э. Баумана)
Влайков Н.Д.
Решение однородных СЛАУ
Методические указания для проведения упражнений
по курсу аналитической геометрии
Калуга 2011г.
Содержание.
Цели занятия стр.4
План занятия стр.4
Необходимые теоретические сведения стр.5
Практическая часть стр.10
Контроль освоения пройденного материала стр.13
Домашнее задание стр.14
Количество часов: 2
Цели занятия:
-
Систематизировать полученные теоретические знания о видах СЛАУ и способах их решения.
-
Получить навыки решения однородных СЛАУ.
План занятия:
-
Кратко изложить теоретический материал.
-
Решить однородную СЛАУ.
-
Найти фундаментальную систему решений однородной СЛАУ.
-
Найти частное решение однородной СЛАУ.
-
Сформулировать алгоритм решения однородной СЛАУ.
-
Проверить выполнение текущего домашнего задания.
-
Провести проверочную работу.
-
Представить тему следующего семинара.
-
Выдать текущее домашнее задание.
Необходимые теоретические сведения.
Ранг матрицы.
Опр.
Рангом
матрицы называют число, которое равно
максимальному порядку среди ее ненулевых
миноров. Ранг матрицы обозначают
![]() .
.
Если квадратная матрица невырождена, то ранг равен ее порядку. Если квадратная матрица вырождена, то ее ранг меньше ее порядка.
Ранг диагональной матрицы равен количеству ее ненулевых диагональных элементов.
Теор.
При транспонировании матрицы ее ранг
не меняется, т.е.
![]() .
.
Теор. Ранг матрицы не меняется при элементарных преобразования ее строк и столбцов.
Теорема о базисном миноре.
Опр.
Минор
![]() матрицы
матрицы
![]() называют
базисным, если выполнены два условия:
называют
базисным, если выполнены два условия:
а) он не равен нулю;
б)
его порядок равен рангу матрицы
![]() .
.
Матрица
![]() может иметь несколько базисных миноров.
может иметь несколько базисных миноров.
Строки
и столбцы матрицы
![]() ,
в которых расположен выбранный базисный
минор, называют базисными.
,
в которых расположен выбранный базисный
минор, называют базисными.
Теор.
Теорема о базисном миноре. Базисные
строки (столбцы ) матрицы
![]() ,
соответствующие любому ее базисному
минору
,
соответствующие любому ее базисному
минору
![]() ,
линейно независимы. Любые строки
(столбцы) матрицы
,
линейно независимы. Любые строки
(столбцы) матрицы
![]() ,
не входящие в
,
не входящие в
![]() ,
являются линейными комбинациями базисных
строк (столбцов).
,
являются линейными комбинациями базисных
строк (столбцов).
Теор. Для любой матрицы ее ранг равен максимальному количеству ее линейно независимых строк (столбцов).
Вычисление ранга матрицы. Метод элементарных преобразований.
С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду. Ранг же ступенчатой матрицы равен количеству ненулевых строк. Базисным в ней является минор, расположенный на пересечении ненулевых строк со столбцами, соответствующими первым слева ненулевым элементам в каждой из строк.
СЛАУ. Основные определения.
Опр.
Система
![]() линейных
алгебраических уравнений с
линейных
алгебраических уравнений с
![]() неизвестными
представляет собой систему вида
неизвестными
представляет собой систему вида
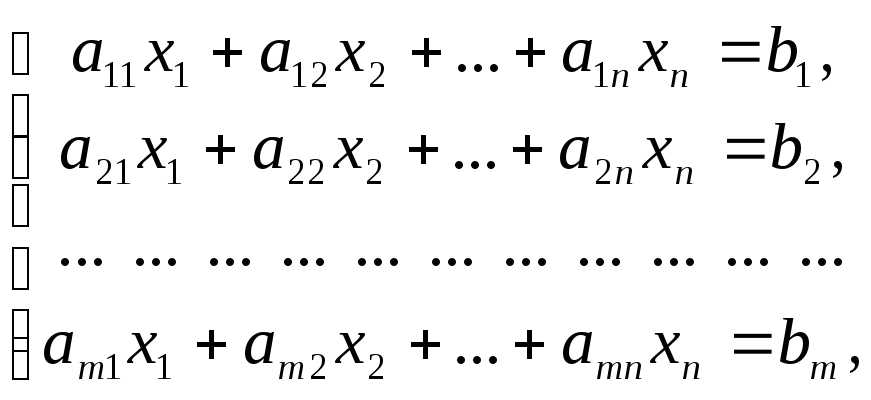 (15.1)
(15.1)
Числа
![]() называют коэффициентами СЛАУ. Числа
называют коэффициентами СЛАУ. Числа
![]() называют свободными членами уравнений.
называют свободными членами уравнений.
Запись СЛАУ в виде (15.1) называют координатной.
Опр.
СЛАУ называют однородной, если
![]() .
Иначе ее называют неоднородной.
.
Иначе ее называют неоднородной.
Опр. решением СЛАУ называют такой набор значений неизвестных, при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ так же называют ее частным решением.
Решить СЛАУ – значит решить две задачи:
- выяснить, имеет ли СЛАУ решения;
- найти все решения, если они существуют.
Опр. СЛАУ называют совместной, если она имеет хотя бы одно решение. В противном случае ее называют несовместной.
Опр. Если СЛАУ (15.1) имеет решение, и притом единственное, то ее называют определенной, а если решение не единственное – то неопределенной.
Опр.
Если в уравнении (15.1)
![]() ,СЛАУ
называют квадратной.
,СЛАУ
называют квадратной.
Формы записи СЛАУ.
Кроме координатной формы (15.1) записи СЛАУ часто используют и друге ее представления.
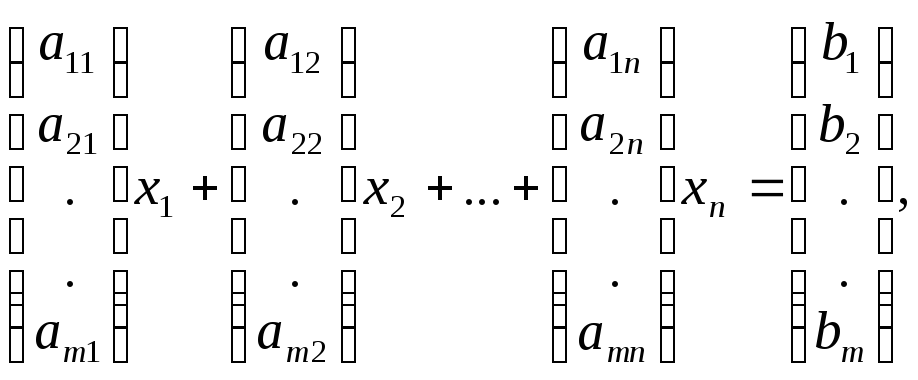 (15.2)
(15.2)
Соотношение называют векторной формой записи СЛАУ.
Если же взять за основу произведение матриц, то СЛАУ (15.1) можно записать так:
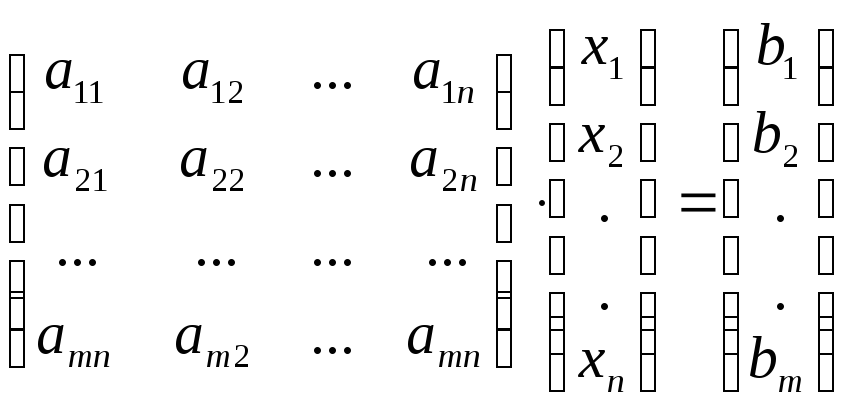 (15.3)
(15.3)
или
![]() .
.
Запись СЛАУ (15.1) в виде (15.3) называют матричной.
Однородные СЛАУ.
Однородная
система
![]() линейных
алгебраических уравнений с
линейных
алгебраических уравнений с
![]() неизвестными
представляет собой систему вида
неизвестными
представляет собой систему вида
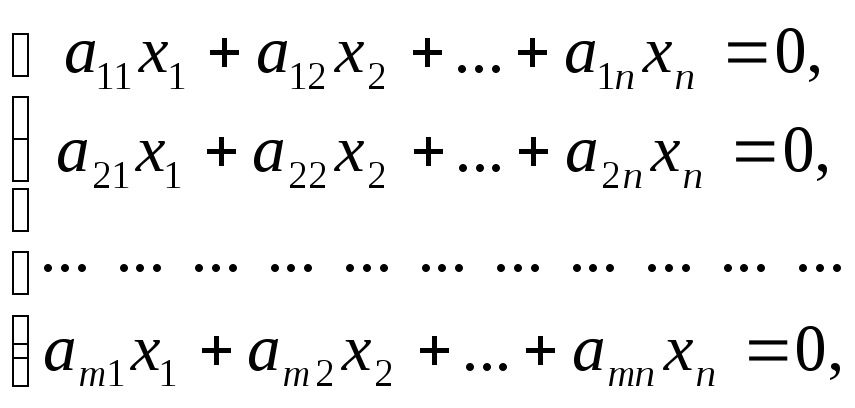
Однородные СЛАУ всегда совместны, поскольку всегда имеется нулевое решение.
Критерий существования ненулевого решения. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы ее матрица была вырождена.
Теор.
Если
столбцы
![]() ,
,
![]() ,
…,
,
…,
![]() - решения однородной СЛАУ, то и любая их
линейная комбинация также является
решением этой системы.
- решения однородной СЛАУ, то и любая их
линейная комбинация также является
решением этой системы.
Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечное множество решений.
Естественно
попытаться найти такие решения
![]() ,
,
![]() ,
…,
,
…,
![]() системы,
чтобы любое другое решение представлялось
в виде их линейной комбинации и притом
единственным образом.
системы,
чтобы любое другое решение представлялось
в виде их линейной комбинации и притом
единственным образом.
Опр.
Любой набор из
![]() линейно
независимых столбцов
линейно
независимых столбцов
![]() ,
,
![]() ,
…,
,
…,![]() ,
являющихся решениями однородной СЛАУ
,
являющихся решениями однородной СЛАУ
![]() ,
где
,
где
![]() -
число неизвестных, а
-
число неизвестных, а
![]() -
ранг ее матрицы
-
ранг ее матрицы
![]() ,
называют фундаментальной системой
решений этой однородной СЛАУ.
,
называют фундаментальной системой
решений этой однородной СЛАУ.
При исследовании и решении однородных систем линейных уравнений в матрице системы будем фиксировать базисный минор. Базисному минору будут соответствовать базисные столбцы и, следовательно, базисные неизвестные. Остальные неизвестные будем называть свободными.
Теор.
О структуре общего решения однородной
СЛАУ. Если
![]() ,
,
![]() ,
…,
,
…,![]() - произвольная фундаментальная система
решений однородной СЛАУ
- произвольная фундаментальная система
решений однородной СЛАУ
![]() ,
то любое ее решение можно представить
в виде
,
то любое ее решение можно представить
в виде
![]() ,
где
,
где
![]() ,
…,
,
…,![]() -
некоторые постоянные.
-
некоторые постоянные.
Т.о. общее решение однородной СЛАУ имеет вид
![]() .
.
Алгоритм решения однородной СЛАУ.
-
Записать матрицу системы.
-
Привести матрицу системы к ступенчатому виду и определить ее ранг.
-
Выбрать базисный минор и базисные неизвестные.
-
Записать однородную СЛАУ, соответствующую полученной матрице.
-
Последовательно выразить базисные неизвестные через свободные.
-
Заменить свободные переменные произвольными постоянными.
-
Записать ответ в виде
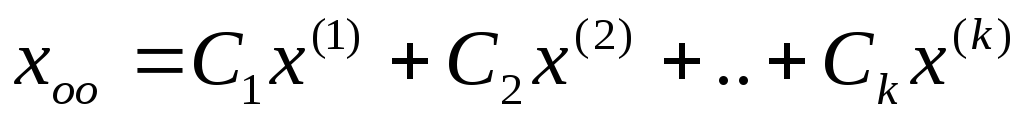 .
.
Практическая часть.
-
Рассмотреть возможные множества решений следующих видов СЛАУ и их графическую интерпретацию.
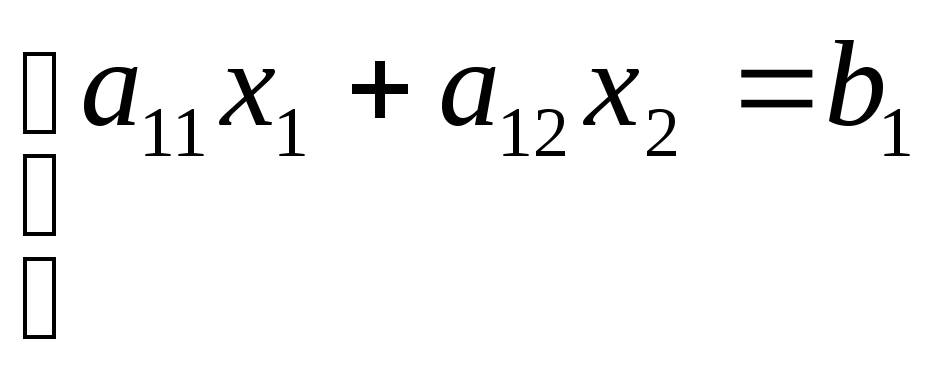 ;
;
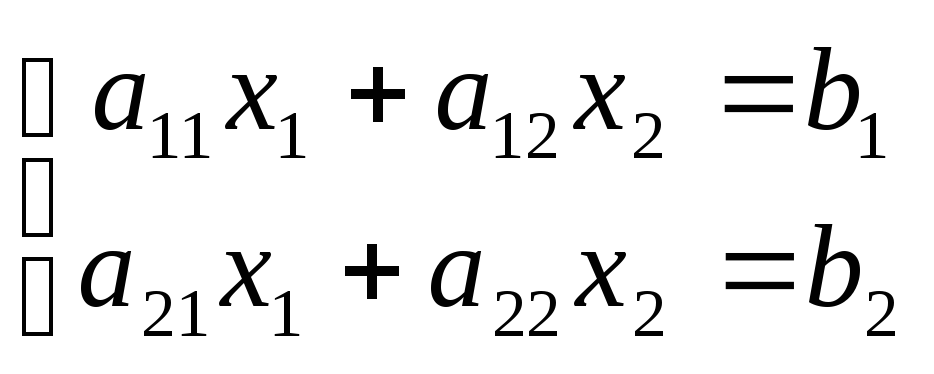 ;
;
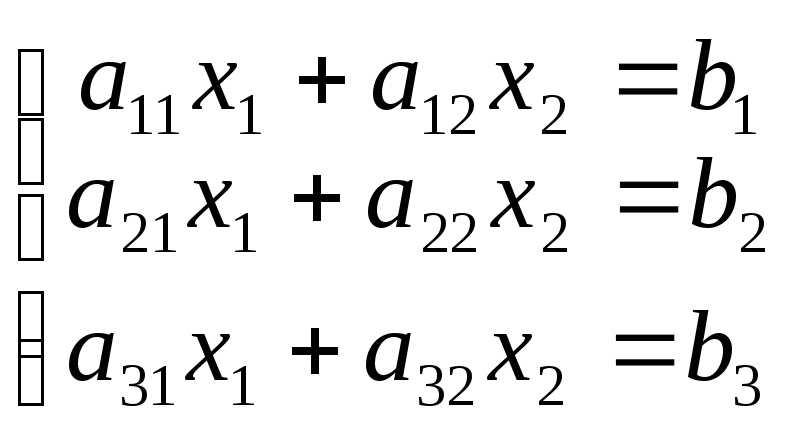 .
.
-
Рассмотреть возможность решения данных систем по формулам Крамера и матричным методом.
-
Изложить суть метода Гаусса.
-
Решить следующие задачи.
Пример 1. Решить однородную СЛАУ. Найти ФСР.
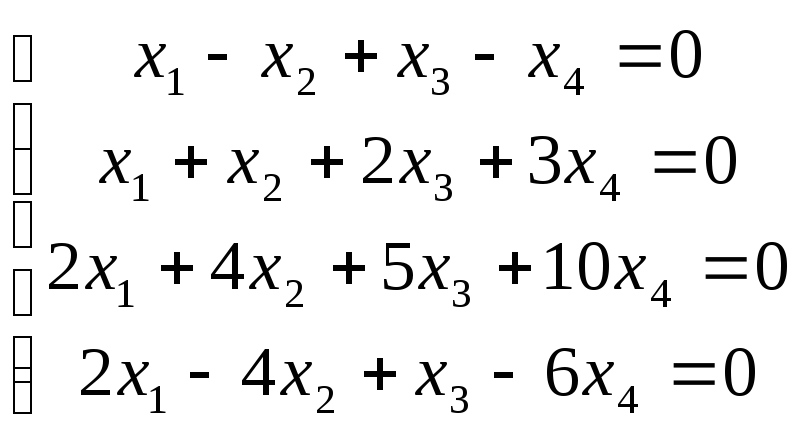 .
.
Запишем матрицу системы и приведем ее к ступенчатому виду.
 .
.
![]() система
будет иметь бесконечно много решений.
ФСР будет состоять из
система
будет иметь бесконечно много решений.
ФСР будет состоять из
![]() столбцов.
столбцов.
Отбросим нулевые строки и снова запишем систему:
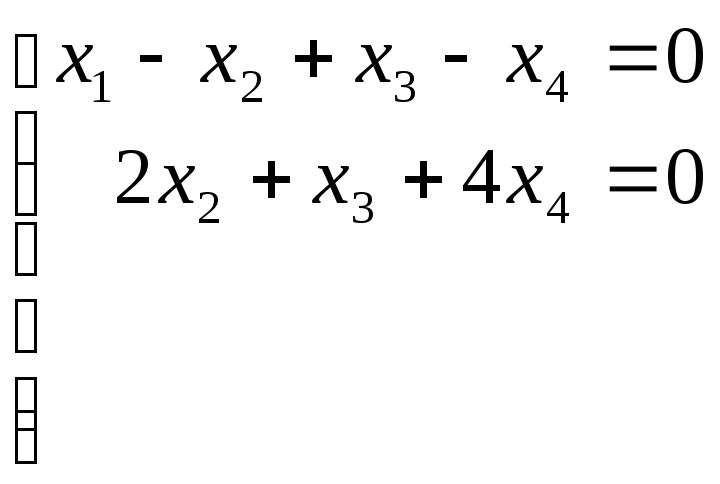 .
.
Будем
считать базисным минор стоящий в левом
верхнем углу. Т.о.
![]() -
базисные неизвестные, а
-
базисные неизвестные, а
![]() -
свободные. Выразим
-
свободные. Выразим
![]() через
свободные
через
свободные
![]() :
:
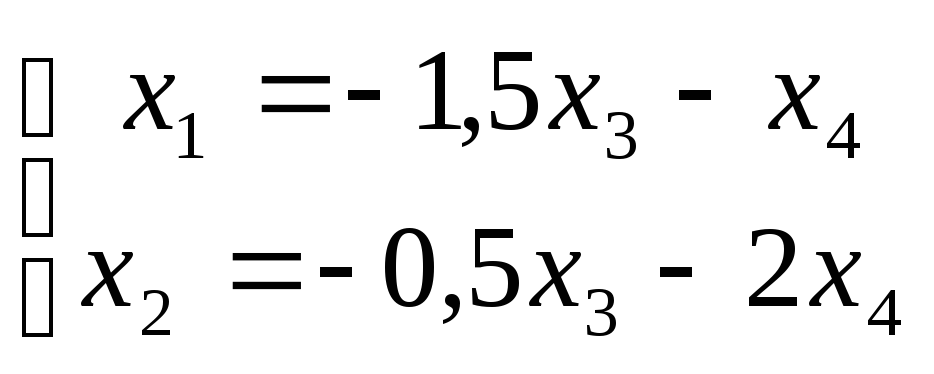 ;
;
Положим
![]() .
.
Окончательно имеем:
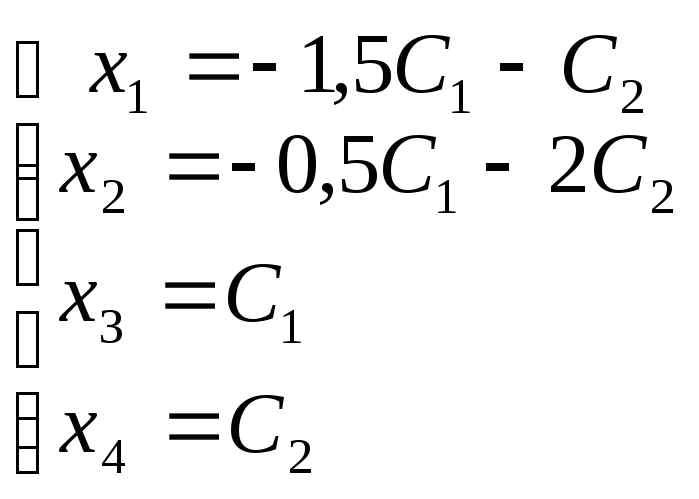 -
координатная форма ответа, или
-
координатная форма ответа, или
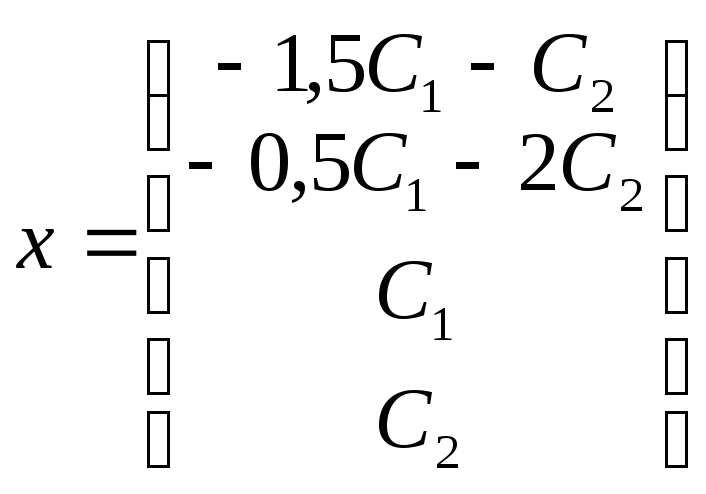 -
матричная форма ответа, или
-
матричная форма ответа, или
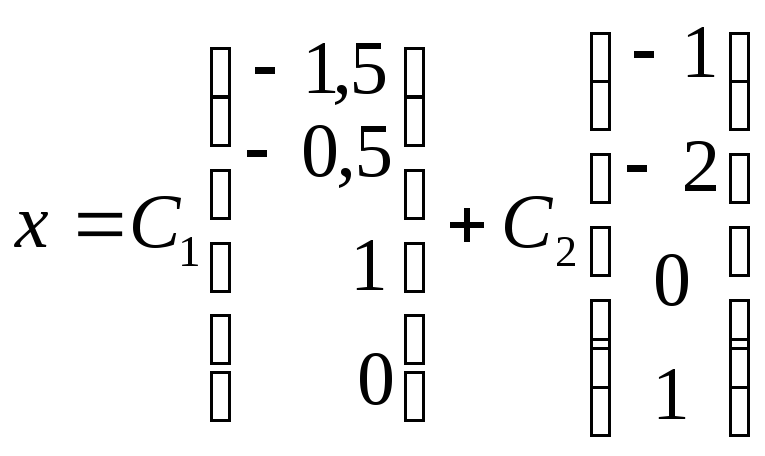 -
векторная форма ответа (вектор - столбцы
являются столбцами ФСР).
-
векторная форма ответа (вектор - столбцы
являются столбцами ФСР).
Алгоритм решения однородной СЛАУ.
-
Записать матрицу системы.
-
Привести матрицу системы к ступенчатому виду и определить ее ранг.
-
Выбрать базисный минор и базисные неизвестные.
-
Записать однородную СЛАУ, соответствующую полученной матрице.
-
Последовательно выразить базисные неизвестные через свободные.
-
Заменить свободные переменные произвольными постоянными.
-
Записать ответ в виде
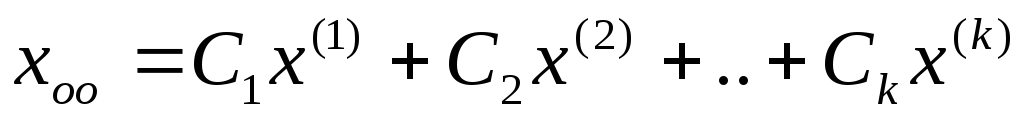 .
.
Найти ФСР и общее решение следующих систем:
№2.225(4.39)
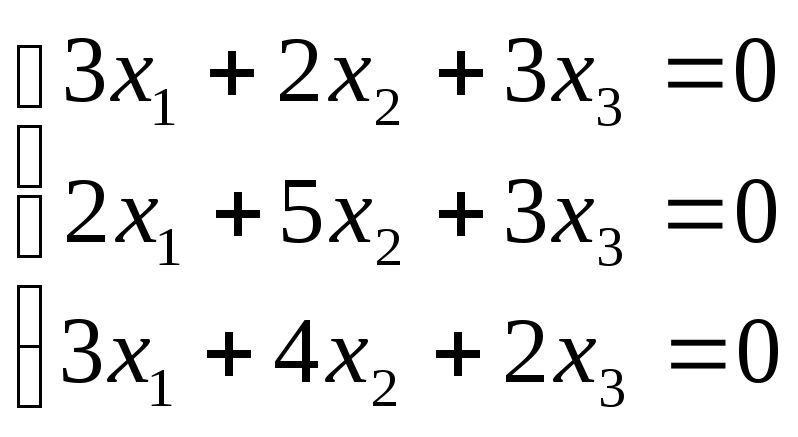 .
Отв.:
.
Отв.:
![]()
№2.223(2.37)
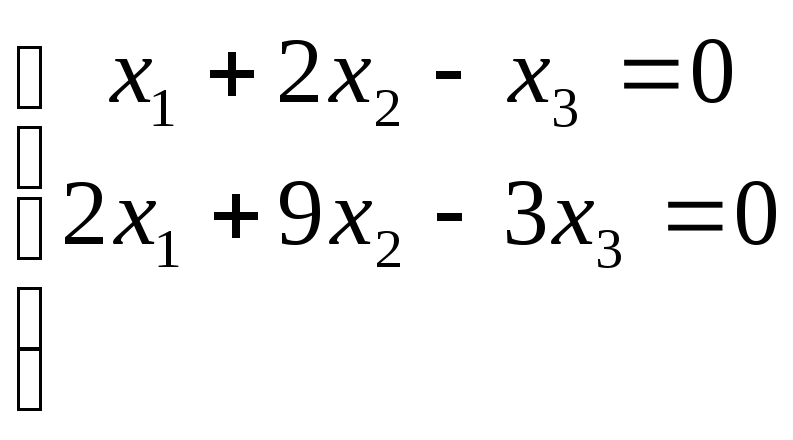 .
Отв.:
.
Отв.:
![]()
№2.227(2.41)
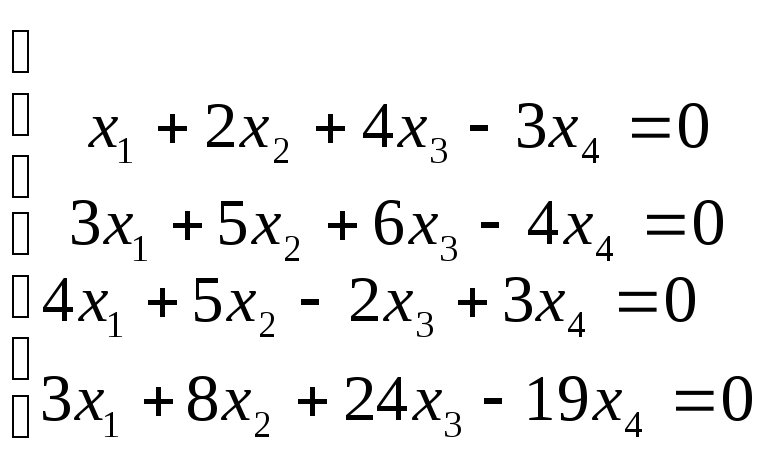 .
Отв.:
.
Отв.:
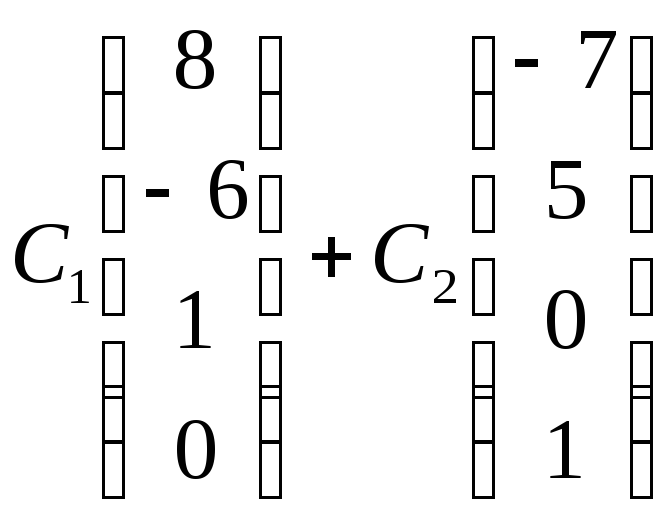
Решить однородную СЛАУ:
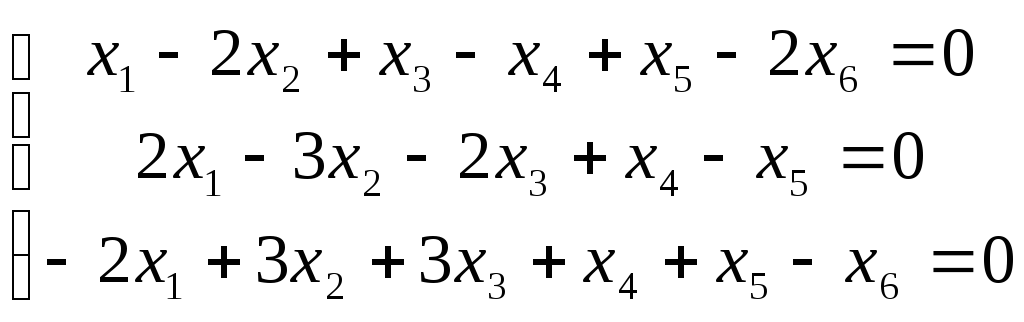 .
Отв.:
.
Отв.:
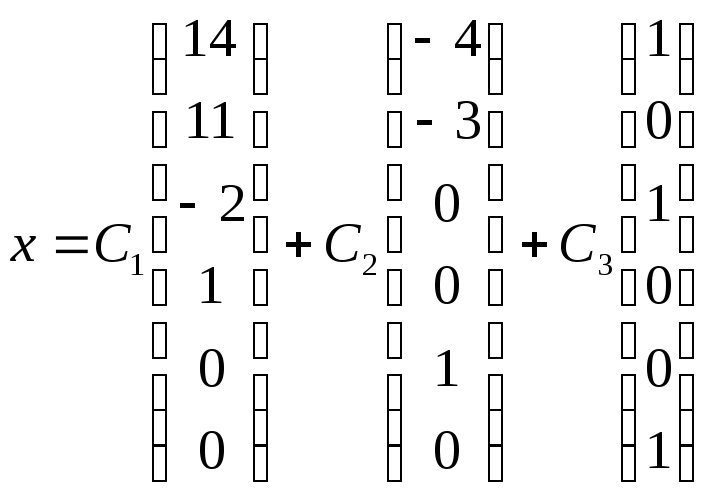
Решить однородную СЛАУ:
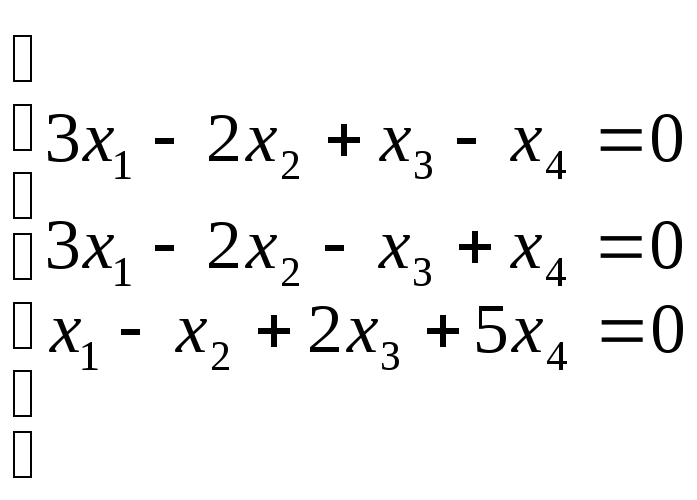 .
Отв.:
.
Отв.:
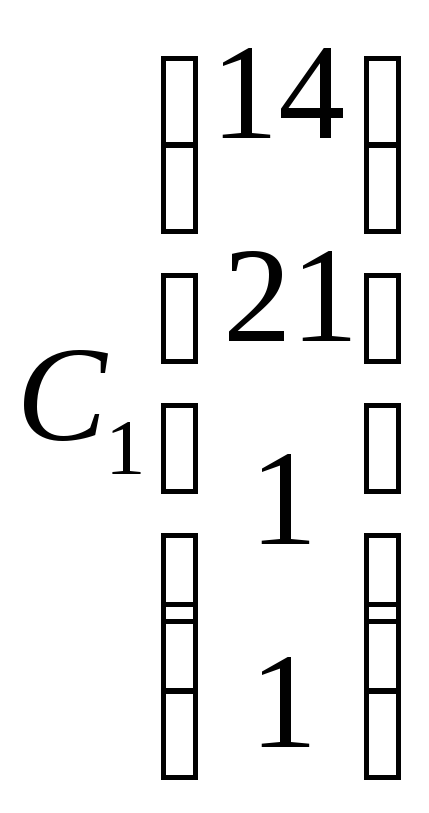
Представление темы следующего семинара.
Решение систем линейных неоднородных уравнений.
Контроль освоения пройденного материала.
Проверочная работа 3 - 5 минут. Участвует 4 студента с нечетными номерами по журналу, начиная с №10
Задание:
|
Вар№1 Выполнить действия:
|
Вар№2 Выполнить действия:
|
|
Вар№3 Найти матрицу обратную данной:
|
Вар№4 Вычислить определитель:
|
Ответы:
|
Вар№1 Выполнить действия:
|
Вар№2 Выполнить действия:
|
|
Вар№3 Найти матрицу обратную данной:
|
Вар№4 Вычислить определитель:
|
Домашнее задание:
1. Решить задачи:
№ 2.224, 2.226, 2.228, 2.230, 2.231, 2.232.
2.Проработать лекции на темы:
Системы линейных алгебраических уравнений (СЛАУ). Координатная, матричная и векторная формы записи. Критерий Кронекера — Капелли совместности СЛАУ. Неоднородные СЛАУ. Критерий существования ненулевого решения однородной СЛАУ. Свойства решений однородной СЛАУ. Фундаментальная система решений однородной СЛАУ, теорема о ее существовании. Нормальная фундаментальная система решений. Теорема о структуре общего решения однородной СЛАУ. Теорема о структуре общего решения неоднородной СЛАУ.