645_Galkina_M.JU._Metody_optimal'nykh_reshenij_

Федеральное агентство связи

Федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет телекоммуникаций и информатики» (СибГУТИ)

М. Ю. Галкина

Методы оптимальных решений

Учебно-методическое пособие

Новосибирск

2016

1

УДК 519.977.5 (075.8)

Утверждено редакционно-издательским советом СибГУТИ

Рецензент доц. В.И. Агульник

иинформатики. – Новосибирск, 2016. – 89 с.

Впособии рассматривается теория и практика применения методов линейного и нелинейного программирования, многокритериальной оптимизации, теории игр в качестве инструмента для принятия решений в экономике. Применение методов иллюстрируется большим количеством примеров. В каждой главе есть вопросы для самопроверки.

Пособие предназначено для студентов заочной формы обучения, обучающихся по направлению 38.03.01 «Экономика», профиль «Финансы и кредит», и изучающих дисциплину «Методы оптимальных решений».

В авторской редакции

©Галкина М.Ю., 2016

©Сибирский государственный университет телекоммуникаций и информатики, 2016

3

ВВЕДЕНИЕ

Несмотря на многообразие задач организационного управления, при их решении можно выделить некоторую общую последовательность этапов, через которые проходит любое исследование. Как правило, это:

1.Постановка задачи.

2.Построение содержательной модели рассматриваемого объекта (процесса). На данном этапе происходит формализация цели управления объектом, выделение возможных управляющих воздействий, влияющих на достижение сформулированной цели, а также описание системы ограничений на управляющие воздействия.

3.Построение математической модели, т.е. перевод сконструированной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.

4.Решение задач, сформулированных на базе построенной математической модели.

5.Проверка полученных результатов на их адекватность природе изучаемой системы, включая исследование влияния так называемых внемодельных факторов, и возможная корректировка первоначальной модели.

6.Реализация полученного решения на практике.

Вкурсе «Методы оптимальных решений» центральное место отведено вопросам, относящимся к четвертому пункту приведенной выше схемы. Это делается не потому, что он является самым важным, сложным или интересным, а потому, что остальные пункты существенно зависят от конкретной природы изучаемой системы, в силу чего для действий, которые должны производиться

вих рамках, не могут быть сформулированы универсальные и содержательные рекомендации.

Для решения экономической задачи математическими методами составляют математическую модель задачи, т.е. записывают ее с помощью математических выражений: неравенств, уравнений и т.п. Для математического описания экономической задачи можно руководствоваться следующей общей схемой:

1)выбирают некоторое количество переменных x1,x2, ,xn , заданием чи-

словых значений которых однозначно определяется одно из возможных состояний исследуемого экономического процесса;

2)выражают взаимосвязи исследуемого экономического процесса в виде математических соотношений (уравнений, неравенств). Эти соотношения образуют систему ограничений математической модели;

3)поиск наилучшего решения формулируют в терминах поиска оптимального (максимального или минимального) значения функции Z(x1,x2, ,xn) .

Построенная функция называется целевой.

В зависимости от свойств целевой функции, математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач. Если Z(x1,x2, ,xn) – линейная функция и линейны функции, описывающие

4

ограничения на переменные x1,x2, ,xn , то математическая модель представляет задачу линейного программирования. Если хотя бы одна из указанных функций нелинейная, то математическая модель является объектом исследования нелинейного программирования. Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач этого раздела разработан целый ряд эффективных алгоритмов и методов.

Математическое моделирование является, с одной стороны, очень важным и сложным, а с другой – практически не поддающимся научной формализации процессом. Заметим, что неоднократно предпринимавшиеся попытки выделить общие принципы создания математических моделей приводили либо к декларированию рекомендаций самого общего характера, трудноприложимых для решения конкретных проблем, либо, наоборот, к появлению рецептов, применимых в действительности только к узкому кругу задач. Поэтому более полезным представляется знакомство с техникой математического моделирования на конкретных примерах.

Мощным инструментом решения задач, построенных на базе математической модели, является наука, которая называется математическое программирование. В данном случае понятие программирование употребляется в смысле планирование (в отличие от программирования для ЭВМ). В свою очередь, в зависимости от вида решаемых задач, в математическом программировании выделяют такие области, как линейное, нелинейное, дискретное, динамическое, стохастическое программирование.

Курс по методам оптимальных решений должен дать студентам достаточное представление о математическом аппарате, используемом при принятии решений в экономических задачах. Освоение этого материала придает студенту уверенность, которой обычно недостает, если он с самого начала направляет свои усилия на изучение философских аспектов и искусства принятия решений.

1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

1.1.Различные формы записи задачи линейного программирования

Рассмотрим задачу линейного программирования (ЗЛП) в общем виде:

j 1

xj 0 ( j 1, ,k,k n),

5

n

Z cjxj max(min).

j 1

Задача линейного программирования задана в канонической форме, если требуется максимизировать целевую функцию, все ограничения системы – уравнения и на все переменные наложено условие неотрицательности.

Задача линейного программирования задана в симметричной форме, если требуется максимизировать целевую функцию, все ограничения системы – неравенства « » (или минимизировать целевую функцию, все ограничения системы – неравенства « ») и на все переменные наложено условие неотрицательности.

Набор чисел X (x1,x2, ,xn) называется допустимым решением (пла-

ном), если он удовлетворяет системе ограничений ЗЛП.

Множество всех допустимых решений называется областью допустимых решений (ОДР).

Допустимое решение X* (x1*,x*2, ,xn*), для которого достигается максимальное (минимальное) значение функции, называется оптимальным планом ЗЛП.

Термины «план» и «оптимальный план» возникли из экономических приложений.

Все три формы записи ЗЛП являются эквивалентными в том смысле, что имеются алгоритмы перехода от одной формы к другой. Таким образом, если имеется способ решения задачи в одной из форм, то всегда можно определить оптимальный план задачи, заданной в любой другой форме. Задача в симметричной форме решается графическим методом, а в канонической форме – сим- плекс-методом.

Рассмотрим алгоритмы перехода от одной формы к другой.

Симметричная каноническая. Переход осуществляется путем добавления в левую часть каждого неравенства дополнительной неотрицательной переменной. Если неравенство было «≤», то балансовая переменная добавляется в левую часть неравенства со знаком «+». Если неравенство было « », то балансовая переменная добавляется в левую часть неравенства со знаком «-». Вводимые новые переменные называются балансовыми. Задачу минимизации функции Z заменяют на задачу максимизации функции (–Z) и используют равенство min Z = –max (–Z).

Каноническая симметричная. Для осуществления такого перехода находится общее решение системы уравнений-ограничений, целевая функция выражается через свободные переменные. Далее, воспользовавшись неотрицательностью базисных переменных, можно исключить их из задачи. Симметричная форма задачи будет содержать неравенства, связывающие только свободные переменные, и целевую функцию, зависящую только от свободных переменных. Значения базисных переменных находятся из общего решения исходной системы уравнений.

6

Общая каноническая. Каждая переменная, на которую не было наложено условие неотрицательности, представляется в виде разности двух новых неотрицательных переменных. Неравенства преобразуются в уравнения путем введения в левую часть каждого неравенства балансовой переменной таким же образом, как это было описано при переходе от симметричной к канонической форме. Задачу минимизации функции Z заменяют на задачу максимизации функции (–Z) таким же образом, как это было описано при переходе от симметричной к канонической форме.

1.2.Графический метод решения задачи линейного программирования

Графический метод применяется для решения ЗЛП, заданной в симметричной форме. Этот метод наиболее эффективно применяется для решения задач с двумя переменными, т.к. требует графических построений. В случае трех переменных необходимы построения в R3, в случае четырех переменных необходимы построения в R4 и т.д.

Множество точек называется выпуклым, если для любых двух точек множества оно содержит отрезок, их соединяющий.

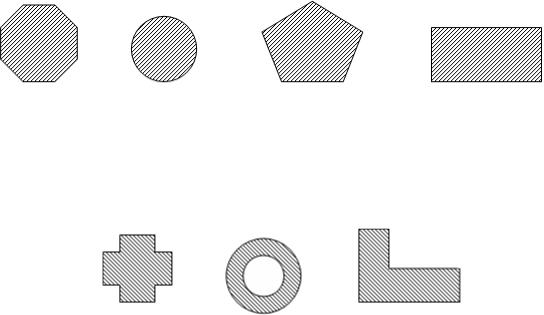
На рис.1 представлены примеры выпуклых множеств. Рис. 1. Выпуклые множества

На рис. 2 представлены примеры множеств, которые не являются выпуклыми.

Рис. 2. Невыпуклые множества Теорема 1 Пересечение любого количества выпуклых множеств является

выпуклым множеством.

Теорема 2 Пусть имеются две произвольные точки P(p1, p2, , pn) и Q(q1,q2, ,qn) в пространстве Rn. Тогда для любой точки X(x1,x2, ,xn) от-

резка [PQ] должно выполняться: xi qi (1 )pi(i 1,2, ,n),.где 0 1. Гиперплоскостью в пространстве Rn называется множество точек, удовле-

творяющее уравнению a1x1 a2x2 anxn b . Заметим, что в двумерном случае гиперплоскостью является прямая.

Полупространством называется множество точек, удовлетворяющее одному из неравенств a1x1 a2x2 anxn b или a1x1 a2x2 anxn b. Гиперплоскость делит точки пространства на два полупространства. В двумерном случае гиперплоскостью является полуплоскость.

Теорема 3 Полупространство является выпуклым множеством.

7

Следствие Пересечение любого количества полупространств является выпуклым множеством.

Многогранником называется пересечение одного или более полупространств. Многогранник в двумерном случае называется многоугольником. На рис. 3 приведены примеры многоугольников.

Ограниченное множество Неограниченное множество

Рис. 3. Примеры многоугольников

Точка выпуклого множества называется угловой, если она не лежит внутри никакого отрезка, соединяющего две другие точки из множества.

Пример 1

Угловыми точками треугольника являются его вершины (их три). Угловыми точками круга являются точки окружности, которая его ограничивает (их бесконечное число).

Угловая точка многогранника называется его вершиной. Рассмотрим ЗЛП, заданную в симметричной форме.

a11x1 a12x2 a1nxn b1,

,

am1x1 am2x2 amnxn bm,

x1,x2, ,xn 0,

Z c1x1 c2x2 cnxn max.

Теорема 4 Оптимальный план ЗЛП соответствует вершине многогранника решений, определяемого ее системой ограничений.

8

Пусть задача линейного программирования с двумя переменными задана в симметричной форме.

a11x1 a12x2 b1,

a21x1 a22x2 b2,

,

am1x1 am2x2 bm,

x1,x2 0,

Z c1x1 c2x2 max.

Для решения этой задачи можно перебрать все вершины многоугольника, определяемого системой ограничений, и выбрать из них ту, в которой значение функции больше. Но можно не перебирать все вершины, а воспользоваться понятиями линии уровня и градиента.

Линией уровня функции Z называется множество точек, удовлетворяющее уравнению Z c , где c – произвольная константа. В двумерном случае это уравнение определяет прямую. Линии уровня образуют семейство параллельных прямых.

Таким образом, наибольшее значение Z достигается в вершине, через которую проходит линия уровня, соответствующая наибольшему значению Z.

Для графического решения задачи ЗЛП используют следующий алгоритм:

1.Записывают уравнения граничных прямых ai1x1+ai2x2=bi (i = 1,…,m) и строят их на плоскости X1OX2 по двум точкам.

2.Отмечают полуплоскости, соответствующие ограничениямнеравенствам. Для этого берут «пробную» точку, через которую не проходит граница полуплоскости (часто берут, если прямая не проходит через начало координат, точку (0,0)) и ее координаты подставляют в соответствующее ограни- чение-неравенство. Если полученное неравенство верное, то искомой будет полуплоскость, содержащая «пробную» точку; в противном случае искомой будет полуплоскость, которой данная точка не принадлежит.

3.Заштриховывают многоугольник, определяемый системой ограничений. Для этого определяют общую часть ранее отмеченных m полуплоскостей, лежащую в первой четверти (следует из условий неотрицательности переменных).

4. Строят вектор grad Z (c1,c2) и одну из прямых семейства Z c (чаще всего Z = 0). Если выбранный для построения многоугольника масштаб не по-

9

5.В случае необходимости параллельным переносом линию уровня следует расположить таким образом, чтобы многоугольник находился впереди линии уровня по направлению grad Z .

6.Определяют экстремальную точку, соответствующую вершине многоугольника путем параллельного перемещения прямой Z = с в направлении вектора grad Z . Это будет наиболее удаленная вершина многоугольника, в кото-

рой линия уровня пересекается с многоугольником.

7. Вычисляют координаты оптимальной точки и значение функции Z в этой точке.

Замечание: Если у функции требуется найти минимальное значение, то линию уровня Z = c перемещают в направлении вектора grad Z (или перемещают в направлении grad Z , но находят первую вершину пересечения линии уровня с многоугольником).

В зависимости от особенностей области допустимых решений и взаимного расположения области и вектора gradZ при решении задачи линейного программирования возможны различные случаи. Рассмотрим их.

1.Если область допустимых решений – ограниченный многоугольник, то может быть либо единственное решение, либо бесконечно много решений – все точки отрезка, соединяющего две вершины многоугольника (альтернативный оптимум). В случае альтернативного оптимума оптимальный план представляется выражением координат произвольной точки отрезка через координаты ее концов.

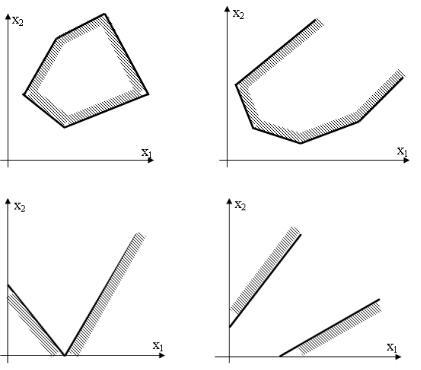
2.Если область допустимых решений – неограниченный многоугольник, то в зависимости от направления gradZ задача может иметь или не иметь

решения. В этом случае также может оказаться альтернативный оптимум. На рис. 4 приведены примеры нахождения оптимальной точки.

10