645_Galkina_M.JU._Metody_optimal'nykh_reshenij_

Рис. 26. Настройка формата данных

В ячейки F5, F6, F7 введем формулы для зависимостей левых частей системы ограничений, а в ячейку D10 – формулу для зависимости целевой функции (рис. 27).

Рис. 27. Ввод формул

2. Далее необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберите команду Поиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить в соответствии с рис. 28 (для добавления ограничений пользуемся кнопкой Добавить).

61

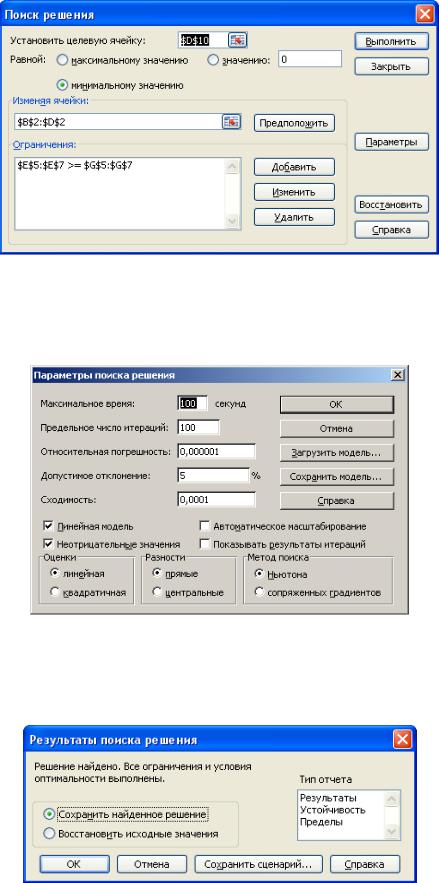
Рис. 28. Настройка «Поиска решений»

Далее нажимаем кнопку Параметры и в появившемся окне Параметры поиска решений устанавливаем флажок Неотрицательные значения, Линейная модель и нажимаем OK (рис. 29).

Рис. 29. Настройка параметров «Поиска решений»

В окне Поиск решения после нажатия кнопки Выполнить появляется окно Результаты поиска решения, в котором выбираем сохранение найденных значений и нажимаем кнопку ОК (рис. 30).

Рис. 30. Сохранение результатов «Поиска решений»

Результаты поиска решений приведены на рис. 31.

62

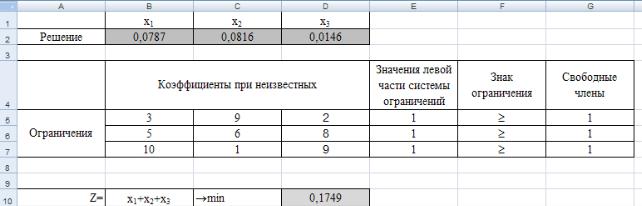
Рис. 31. Найденное оптимальное решение для ЗЛП игрока A

преобразованной матрицей. Для исходной матрицы компоненты смешанной стратегии не меняются, а цена игры меньше на число, кото-

ния для игрока В. Средний проигрыш игрока В должен быть не больше цены игры при любом поведении игрока А. Получаем систему линейных ограниче-

=+ + → max.

Решим задачу средствами табличного редактора MS Excel, с использовани-

ем настройки Поиск решения.

63

1. Подготовим данные на листе (рис. 32).

Рис. 32. Подготовка данных на листе Excel для решения ЗЛП для игрока B

В ячейки F5, F6, F7 введем формулы для зависимостей левых частей системы ограничений, а в ячейку D10 – формулу для зависимости целевой функции.

2. Далее необходимо воспользоваться надстройкой Поиск решения.

Рис. 33. Настройка «Поиска решений»

В окне Параметры поиска решений устанавливаем флажок Неотрицательные значения. Результаты «Поиска решений» приведены на рис. 34.

Рис. 34. Найденное оптимальное решение для ЗЛП игрока B

64

2.2.6.Игры с природой

Врассмотренных ранее задачах теории игр предполагалось, что в них принимают участие 2 участника, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша или уменьшение проигрыша. Однако во многих задачах теории игр отсутствует информация об условиях, в которых осуществляется действие. Эти условия зависят не от сознательного действия другого игрока, а от объективной действительности, которую принято называть природой. Такие игры называются играми с природой. Под термином «природа» понимается весь комплекс внешних условий, в которых человеку приходится принимать решение. Природа безразлична к выигрышу и не стремится обратить в свою пользу промахи человека. В играх с природой игрок А – человек или группа лиц, объединенных общностью цели, который называется статистиком. Возможные стратегии природы определяются как ее состояния (например, условия погоды, спрос на продукцию). Человеку могут быть известны вероятности, с которыми природа реализует свои состояния.

Пусть статистик может использовать m стратегий А1, А2, …, Аm, а природа может реализовывать n различных состояний Р1, Р2, …, Рn. Условия игры с при-

родой также задаются платежной матрицей

шем, который получил бы статистик, если бы достоверно знал, что природа будет находиться в состоянии Pj, и выигрышем аij, который он получит, используя

Рассмотрим критерии выбора оптимальной стратегии. 1. Критерий недостаточного основания Лапласа

Все состояния природы считаются равновероятными. В качестве оптимальной принимается чистая стратегия, при которой максимизируется средний

2.Максиминный критерий Вальда

Вкачестве оптимальной выбирается стратегия, при которой наименьший выигрыш статистика будет максимальным, т.е. равен нижней цене игры для

3.Критерий минимаксного риска Сэвиджа

Вкачестве оптимальной выбирается стратегия, при которой минимизиру-

новки. Следующий критерий учитывает, как пессимистический, так и оптимистический подход к ситуации.

4. Критерий Гурвица

Принимается решение о выборе стратегии, при которой достигается max { min +(1 − )max }, где 0 1. Значение выбирают на основе субъективных соображений. Чем больше желание подстраховаться, тем ближе к 1 значение .

Обычно анализ практических ситуаций проводится по нескольким критериям одновременно, что позволяет выбрать наиболее обоснованное решение.

Пример 17

Сельскохозяйственное предприятие планирует посадить некоторую сельскохозяйственную культуру двух сортов. Посевная площадь – 1 га. Сорта отличаются друг от друга требованиями к влаге во время вегетационного периода. Проанализировав погодные условия, выделены 4 состояния погоды (S1, S2, S3, S4), отличающиеся режимом осадков. Средняя урожайность (ц/га) каждого сорта на всем участке для каждого состояния погоды приведена в таблице:

Возможные варианты посева:

А1 – сорт 1 посадить на 100 % площади; А2 – сорт 1 посадить на 75 % площади, сорт 2 посадить на 25 % площади;

А3 – сорт 1 посадить на 50 % площади, сорт 2 посадить на 50 % площади; А4 – сорт 1 посадить на 25 % площади, сорт 2 посадить на 75 % площади; А5 – сорт 2 посадить на 100 % площади.

Определить оптимальную стратегию с помощью критериев недостаточного основания Лапласа, максиминного критерия Вальда, критерия минимаксного риска Сэвиджа, пессимизма-оптимизма Гурвица (коэффициент пессимизма взять равным 0,4).

Решение

Составим платежную матрицу игры. Рассчитаем ее элементы:

= 23;

66

=29;

=31;

=37;

=23∙0,75+36∙0,25 = 26,25;

=29∙0,75+33∙0,25 = 30;

=31∙0,75+28∙0,25 = 30,25;

=37∙0,75+24∙0,25 = 33,75;

=23∙0,5+36∙0,5 = 29,5;

=29∙0,5+33∙0,5 = 31;

=31∙0,5+28∙0,5 = 29,5;

=37∙0,5+24∙0,5 = 30,5;

=23∙0,25+36∙0,75 = 32,75;

=29∙0,25+33∙0,75 = 32;

=31∙0,25+28∙0,75 = 28,75;

=37∙0,25+24∙0,75 = 27,25;

=36;

=33;

=28;

=24.

1 = 4(23+29+31+37) = 30;

1 = 4(26,25+30+30,25+33,75) ≈ 30,06;

1 = 4(29,5+31+29,5+30,5) ≈ 30,13;

1 = 4(32,75+32+28,75+27,25) ≈ 30,19;

67

1 = 4(36+33+28+24) = 30,25.

Найденные значения заносим в соответствующий столбец и выбираем максимальное = max(30;30,06;30,13;30,19;30,25) = 30,25, значит, опти-

мальной по данному критерию является стратегия А5.

2. Максиминный критерий Вальда

В каждой строке находим минимальный элемент: = min и вы-

бираем максимальное = max(23;26,25;29,5;27,25;24) = 29,5, значит, оп-

тимальной по данному критерию является стратегия А3.

3. Критерий минимаксного риска Сэвиджа

Рассчитаем матрицу рисков. В каждом столбце находим максимальный

Заполним матрицу рисков по столбцам. Для этого вычитаем из j все остальные элементы столбца, результаты записываем на соответствующих местах

= 0,4∙23+0,6∙37 = 31,4;

68

=0,4∙26,25+0,6∙33,75 = 30,75;

=0,4∙29,5+0,6∙31 = 30,4;

=0,4∙27,25+0,6∙32,75 = 30,55;

=0,4∙24+0,6∙36 = 31,2.

критерию является стратегия А .

Ответ:

1)Стратегия А1 является оптимальной согласно критерию пессимизмаоптимизма Гурвица.

2)Стратегии А2, А4 не являются оптимальными ни по одному из критери-

ев.

3)Стратегия А3 является оптимальной согласно пессимистическим критериям Вальда и Сэвиджа.

4)Стратегия А5 является оптимальной согласно критерию Лапласа.

Вопросы для самопроверки

1.Сформулируйте постановку задачи о назначениях с минимизацией, максимизацией функции? В чем отличия в их решениях?

2.В чем заключается алгоритм венгерского метода решения задачи о назначениях?

3.Что такое стратегия игрока? Какая игра называется парной с нулевой суммой?

4.Что такое платежная матрица?

5.Как определить верхнюю и нижнюю цену игры? Каково соотношение между ними?

6.Какая игра имеет седловую точку? Что означает решение игры в чистых стратегиях?

7.Что такое оптимальная смешанная стратегия?

8.Сформулируйте основную теорему теории игр – теорему Фон-Неймана.

9.Как можно графически решить игру?

10.На чем основана связь матричной игры и ЗЛП? 11.В чем отличие игр с природой?

12.Перечислите основные критерии решения игр с природой.

3. МНОГОЦЕЛЕВЫЕ ЗАДАЧИ

Задачи, решаемые с учетом множества показателей или критериев, носят название многоцелевых. При решении таких задач необходимо найти такой план, при котором система критериев была бы наилучшей. Если все критерии равнозначны, то эффективным считается такой план, при котором отклонения от оптимумов по каждому критерию равны.

С привычной точки зрения задача со многими критериями решения не имеет – далеко не всегда есть возможность одновременного удовлетворения всех заданных условий. Поэтому, когда говорят о решении многокритериальной задачи, имеют в виду какой-нибудь компромисс между изначально противоречивыми требованиями. А так как практически любая подобная ситуация

69

допускает разные компромиссные разрешения, то и подходы к их поиску многочисленны и весьма разнообразны. Перечислим некоторые подходы.

Метод уступок – лицо, принимающее решения, подводится к выбору решения путем постепенного ослабления первоначальных требований, как правило, одновременно невыполнимых.

Метод идеальной точки – в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайший к наилучшему, как правило, недосягаемому (в так называемой точке утопии).

Метод свертывания – лицо, принимающее решения, сводит многокритериальную задачу к задаче с одним критерием.

Метод ограничений – множество допустимых значений неизвестных уменьшается путем осмысленного введения дополнительных ограничений на заданные критерии.

Метод анализа иерархий – на основании суждений экспертов оценивается вклад в общую оценку каждого критерия.

Далее будем рассматривать случаи, когда решение принимается по двум критериям.

3.1.Множество Парето

Рассмотрим на плоскости (U, V) произвольное множество . Каждая точка плоскости обладает одним из следующих трех свойств: либо все точки, ближайшие к ней, принадлежат множеству (такая точка называется внутренней точкой множества ), либо все точки, ближайшие к ней, множеству не принадлежат (такая точка называется внешней точкой по отношению к множеству), либо сколь угодно близко от нее расположены как точки множества , так и точки, множеству не принадлежащие (такие точки называются граничными точками множества ) (рис. 35). Множество всех граничных точек множества называется его границей.

Рис. 35. Свойства точек множества Точки множества можно разбить на три класса (рис. 36):

- к первому классу относятся точки, которые, оставаясь во множестве , можно сдвинуть так, чтобы одновременно увеличились обе координаты (в этот класс попадают все внутренние точки множества и часть его граничных точек);

- второй класс образуют граничные точки, перемещением которых по границе можно увеличить только одну из координат при сохранении значения

70