645_Galkina_M.JU._Metody_optimal'nykh_reshenij_

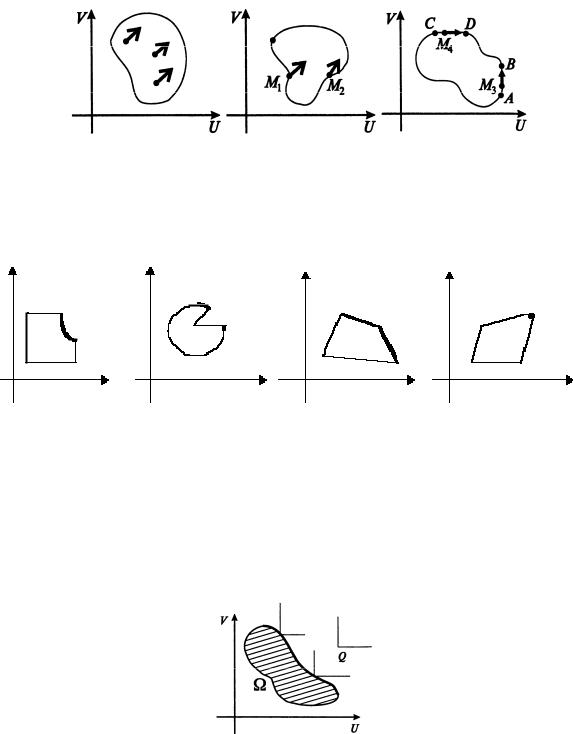
второй (вертикальный отрезок АВ и горизонтальный отрезок CD на границе множества );

- в третий класс попадут граничные точки, перемещение которых по границе уменьшает одну из координат при одновременном увеличении другой (дуга BD границы ).

Рис. 36. Разбиение множества на классы

Множество точек третьего класса принято называть границей (множеством) Парето данного множества .

На рис. 37 приведены примеры границ Парето некоторых простейших множеств.

Рис. 37. Примеры границ Парето для различных множеств

Говоря нестрого, граница Парето множества – это точки, из которых нельзя сдвинуться на «север», «восток» либо «северо-восток», оставаясь в том же множестве .

Другими словами, в множество Парето не включаются такие решения, которые могут быть улучшены одновременно по обоим критериям.

Укажем простое геометрическое правило, посредством которого можно выделять из заданного плоского множества его границу Парето (рис. 38).

Рис. 38. Определение границы Парето Рассмотрим пробный прямой угол, стороны которого сонаправлены коор-

динатным осям U и V. Положение этого пробного угла на плоскости однозначно определяется его вершиной Q. Перемещая пробный угол (параллельно самому себе), мы будем собирать только те точки заданного множества ,

71

которые можно совместить с точкой Q так, чтобы ни одна другая точка множества не попадала ни внутрь этого угла, ни на одну из его сторон. Совокупность всех таких точек и будет искомой границей Парето для множества .

3.2.Метод идеальной точки

Рассмотрим постановку двухкритериальной задачи в общем виде. Пусть на плоскости (х,y) задано множество ω (рис. 39) и в каждой точке этого множества определены две непрерывные функции: U = Φ(x,y) и V = Ψ(x,y). На множестве ω требуется найти точку (x0, y0), в которой Φ(x0,y0)=max и Ψ(x0,y0)=max.

Рис. 39. Задание множества, на котором определены функции U и V

Сразу же отметим, что в общем случае поставленная задача решения не имеет. В самом деле, изобразим на плоскости (U, V) все точки, координаты которых вычисляются по формулам U = Φ(x,y) и V = Ψ(x,y). Обозначим полученное множество через . Из рис. 40 видно, что Umax (наибольшее значение U) и Vmax (наибольшее значение V) достигаются в разных точках, а точка P с координатами (Umax, Vmax) лежит вне множества . Таким образом, в исходной постановке задача, вообще говоря, неразрешима – удовлетворить обоим требованиями одновременно невозможно. И, следовательно, нужно искать какое-то компромиссное решение.

Рис. 40. Нахождение максимумов функций U и V

Метод идеальной точки использует множество Парето, составленное из допустимых точек задачи, которые не могут быть «сдвинуты» в пределах допустимого множества с улучшением сразу по обоим критериям. На границе Парето отыскиваются точки, ближайшие к точке утопии P (точка утопии дает сочетание наилучших значений всех критериев, но обычно не удовлетворяет заданным ограничениям).

Рассмотрим реализацию метода идеальной точки на конкретном примере.

Пример 18

72

Решить двухкритериальную задачу линейного программирования методом идеальной точки.

−≤ 3,

≥0, ≥ 0,

Решение

1. Построим область допустимых решений в плоскости xOy, определяемую системой неравенств.

Каждое линейное неравенство на плоскости задает полуплоскость, все точки которой обращают неравенство в верное числовое неравенство. Рассмотрим первое неравенство 4y – x ≤ 20. Границей полуплоскости является прямая 4y – x = 20. Построим эту прямую по двум точкам (рис. 41). Составим таблицу для построения прямой:

Определим, какую полуплоскость задает первое неравенство: выше построенной прямой или ниже ее. Для этого подставим в неравенство координаты любой «пробной» точки, не лежащей на построенной прямой. Возьмем в качестве «пробной точки» начало координат: (0; 0):

4 − ≤ 20, 4∙0 −0 ≤ 20, 0 ≤ 20.

Получили верное числовое неравенство. Следовательно, рассматриваемое линейное неравенство определяет полуплоскость, которой принадлежит начало

73

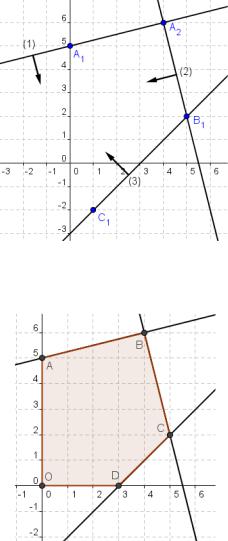
Рис. 41. Графическое решение неравенств системы примера 18

Оставшиеся ограничения: х ≥ 0, у ≥ 0 задают первую координатную четверть. Область допустимых решений – многоугольник OABCD (рис. 42).

Рис. 42. Область допустимых решений системы неравенств примера 18

2. Построим в критериальной плоскости область, соответствующую области допустимых решений OABCD. Для этого необходимо найти координаты вершин.

В нашем случае очевидно, что O(0; 0), A(0; 5), B(4; 6), C(5; 2), D(3; 0), т.к.

часть этих точек использовалась при построении прямых. В общем случае координаты точки пересечения двух прямых определяют совместным решением их уравнений: например, для точки С, которая является точкой пересечения (2)

и (3) прямых необходимо решить систему:

4 + = 22,

−= 3 .

Таким образом, D(3; 0) → D (6; –6).

По найденным координатам точек построим в критериальной плоскости UOV образ многоугольника OABCD – многоугольник O A B C D (рис. 43).

Рис. 43. Образ области допустимых решений в плоскости UOV

3. В критериальной плоскости найдем границу Парето – северо-восточную границу области O A B C D (рис. 44). Граница Парето – ломаная O D C .

Рис. 44. Граница Парето

Точкой утопии, в которой достигается максимум одновременно по двум критериям U и V, является точка P (рис. 45). Через самую высокую (северную) точку области O A B C D провели горизонтальную прямую (через точку O ) и через самую правую (восточную) точку области O A B C D провели вертикальную прямую (через точки C и D ); точка – точка пересечения горизонтальной и вертикальной прямой.

75

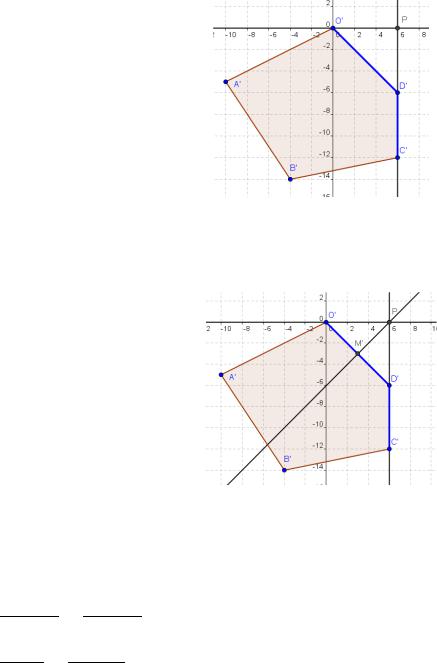
Рис. 45. Нахождение точки утопии

4. На границе Парето найдем идеальную точку – точку, наиболее близко расположенную к точке утопии. В нашем случае это основание перпендикуляра, опущенного из точки утопии Р на отрезок O D – точка M (рис. 46).

Рис. 46. Нахождение идеальной точки

Найдем координаты точки M . Для этого найдем уравнение прямой O D . Воспользуемся уравнением прямой, проходящей через две точки: (0; 0), D (6; –6):

Таким образом, М (3; –3), а значит, компромиссное решение позволит достигнуть значений целевых функций: U = 3, V = –3.

5. Найдем координаты точки в плоскости xOy, которой соответствует точка М критериальной плоскости. Для этого решим систему уравнений:

принадлежит отрезку OD (рис. 47).

Рис. 47. Решение, найденное методом идеальной точки

Ответ: M (1,5; 0), Umax (1,5; 0) = 3, V max (1,5; 0)= –3.

Вопросы для самопроверки

1.Какая задача называется многоцелевой?

2.Каким свойством обладают точки множества Парето?

3.Как найти множество Парето?

4.Что такое точка утопии?

5.В чем суть метода идеальной точки? Какая точка называется идеальной?

4.НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Вобщем случае задача нелинейного программирования (НП) состоит в нахождении экстремума (минимума или максимума) функции

Z = f(x1,…, xn) min (max).

на множестве, задаваемом ограничениями в виде равенств и (или) неравенств:

Также могут быть условия неотрицательности переменных.

Предполагается, что среди функций f и gi (i 1, m) есть хоть одна нелиней-

ная.

Любой n-мерный вектор x = (x1,…,xn), удовлетворяющий ограничениям задачи, называется допустимым решением, а множество X всех таких векторов –

областью допустимых решений (ОДР).

77

Перечислим свойства задач НП, которые существенно усложняют процесс их решения по сравнению с задачами линейного программирования:

1.Множество допустимых решений может иметь очень сложную структуру (например, быть невыпуклым или несвязным).

2.Глобальный максимум (минимум) может достигаться как внутри области, так и на ее границах (где он, вообще говоря, будет не совпадать ни с одним из локальных экстремумов).

3.Целевая функция f может быть недифференцируемой, что затрудняет применение классических методов математического анализа.

Этим объясняется отсутствие общих методов, подобных симплекс-методу

влинейном программировании, позволяющих решать любые задачи НП. Тем не менее отдельные специальные классы нелинейных задач хорошо изучены.

4.1.Графическое решение задачи нелинейного программирования

Графический метод можно использовать для решения задачи НП, которая содержит две переменные х1 и х2, например, задачи следующего вида:

Z = f(x1, x2) → min (max),

gi(x1, x2) ≤ bi, i 1, m.

Чтобы найти ее оптимальное решение, нужно выполнить следующие действия:

1.Найти ОДР, определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения.

2.Построить семейство линий уровня целевой функции f (х1, х2) = C при различных значениях числового параметра С.

3.При решении задачи на минимум определить направление убывания, а для задачи на максимум – направление возрастания линий уровня целевой функции.

4.Найти точку ОДР, через которую проходит линия уровня с наименьшим

взадаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра С. Эта точка будет оптимальным решением. Если целевая функция не ограничена снизу в задаче на минимум (сверху – в задаче на максимум), то это означает, что задача не имеет оптимального решения.

5.Найти координаты точки оптимума и определить в ней значение целевой функции.

Отметим, что в отличие от задачи линейного программирования точка оптимума в задаче НП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества.

Пример 19

Найти максимальное и минимальное значение функции

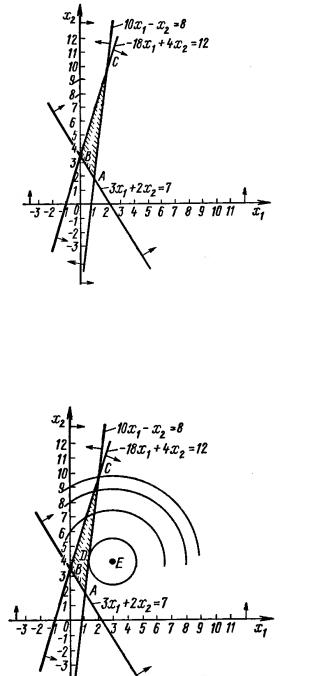
Это задача НП, т.к. целевая функция нелинейна.

Областью допустимых решений является треугольник АВС (рис. 48).

Рис. 48. Нахождение области допустимых решений

достигается в точке D – точке касания окружности и области, максимальное значение функция принимает в точке С – угловой точке множества (рис. 49).

изводную неявной функции). Продифференцируем по x1 обе части уравнения окружности:

4.2.Метод множителей Лагранжа

Рассмотрим частный случай задачи НП, предполагая, что система ограничений содержит только уравнения, отсутствуют условия неотрицательности и функции f(x1,…, xn) и gi (x1,…, xn) непрерывны вместе с частными производными

L(x, λ) = L(x1,…, xn, λ1,…, λm) = f(x1,…, xn) + λi (bi – gi (x1,…, xn)),

i 1

находят частные производные функции Лагранжа по всем переменным xj и λi и приравнивают их нулю для нахождения стационарных точек функции Лагранжа. Получается система n + m уравнений:

Находятся решения этой системы. Среди этих решений после дополнительного анализа (проверки достаточного признака экстремума) отбираются такие, которые действительно являются точками локального оптимума. После сравнения значений целевой функции в этих точках находится точка, являющаяся глобальным оптимумом.

Подчеркнем, что основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безус-

80