645_Galkina_M.JU._Metody_optimal'nykh_reshenij_

ловной и, соответственно, расширить арсенал доступных средств решения проблемы. Однако нетрудно заметить, что задача решения системы уравнений, к которой сводится данный метод, в общем случае не проще исходной проблемы поиска экстремума. Методы, подразумевающие такое решение, называются непрямыми. Они могут быть применены для весьма узкого класса задач, для которых удается получить линейную или сводящуюся к линейной систему уравнений. При решении конкретных практических задач обычно используются прямые методы, основанные на итерационных процессах вычисления и сравнения значений оптимизируемых функций. К таким методам относят градиентные методы решения задач безусловной оптимизации.

4.3.Решение задач выпуклого программирования

Рассмотрим задачу НП:

Z = f(x1,…, xn) min (max);

пары точек x, y Х и любого числа α (0, 1) справедливо соотношение f(α x + (1 – α) y) ≤ α f(x) + (1 – α) f(y).

Функция f называется вогнутой на выпуклом множестве Х, если для любой пары точек x, y Х и любого числа α (0, 1) справедливо соотношение

f(α x + (1 – α) y) ≥ α f(x) + (1 – α) f(y).

Функция f называется строго выпуклой (строго вогнутой), если неравенства в соотношениях являются строгим для всех x ≠ y, т.е. знак неравенства –«<» (соответственно, «>»).

Очевидно, что если f – выпуклая функция, то g = –f – вогнутая функция. Сумма выпуклых (вогнутых) функций – выпуклая (вогнутая) функция. Линейная функция является как выпуклой, так и вогнутой функцией.

Простейший пример выпуклой функции: z = х2, а вогнутой: z = 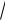х. Множество допустимых решений задачи НП удовлетворяет условию регу-

лярности, если существует, по крайней мере, одна точка Xi из ОДР такая, что gi(Xi)<bi.

Задача НП является задачей выпуклого программирования, если она удов-

летворяет следующим условиям:

1)целевая функция f – выпукла (вогнута);

2)все функции gi в ограничениях выпуклые.

Легко проверить, что если g – выпуклая (вогнутая) функция, то для любого числа b множество {х | g(x) ≤ (≥) b} – выпуклое. Поэтому ОДР в задаче выпуклого программирования – выпуклое множество. Выпуклым будет и множество оптимальных решений. Если же ЦФ – строго выпуклая (вогнутая) функция, то множество точек ее минимума (максимума) состоит из единственной точки.

Наиболее важное свойство таких задач: любая точка локального оптимума задачи выпуклого программирования является точкой ее глобального оптимума. Поэтому в задаче выпуклого программирования можно говорить об опти-

81

мальном решении, не уточняя, идет речь о глобальном или локальном оптимуме.

Составим функцию Лагранжа для задачи выпуклого программирования:

Лагранжа.

Если предположить, что функции f и gi непрерывно дифференцируемы, то можно записать условия Куна–Таккера, определяющие необходимые и доста-

телен, то соответствующее ему ограничение в точке оптимума обязательно должно быть равенством. Если же ограничение не является равенством в точке оптимума, то его множитель Лагранжа равен нулю. Это условие аналогично условию дополняющей нежесткости в задаче линейного программирования.

В отличие от классической задачи условной оптимизации на множители Лагранжа накладывается условие неотрицательности.

Множители Лагранжа допускают интерпретацию, аналогичную интерпретации оптимальных оценок ограничений в задаче линейного программирования. Так, множитель Лагранжа i-го ограничения характеризует величину изменения оптимального значения целевой функции при увеличении правой части этого ограничения на единицу и фиксированных значениях остальных ограничений.

Однако в отличие от задачи линейного программирования величина i* не равна в точности изменению оптимального значения целевой функции при уве-

82

личении правой части i-го ограничения на единицу, а дает лишь приближенную оценку этого изменения.

Пример 20

Решить задачу выпуклого программирования средствами MS Excel.

Проверить выполнение условий Куна–Таккера для найденной оптимальной точки.

Решим задачу с использованием настройки Поиск решения. Для решения нашей задачи создадим в Excel книгу с именем «Решение задачи нелинейного программирования». Подготовим данные на листе (рис. 50).

Сначала определим ячейки, в которые будет помещен результат решения. Пусть это будут ячейки В2, С2, сделаем у них заголовки. В этих ячейках нет данных, их должен будет рассчитать Excel, они выделены цветом. Далее заполним коэффициенты при неизвестных и правые части системы ограничений (строки 5 – 7). Заведем строку 9 для целевой функции. Цветом выделена ячейка, в которой будет находиться значение целевой функции для найденного оптимального решения.

Рис. 50. Подготовка данных для примера 20

В ячейки D5, D6, D7 введем формулы для зависимостей левых частей системы ограничений, а в ячейку E9 – формулу для зависимости целевой функции.

83

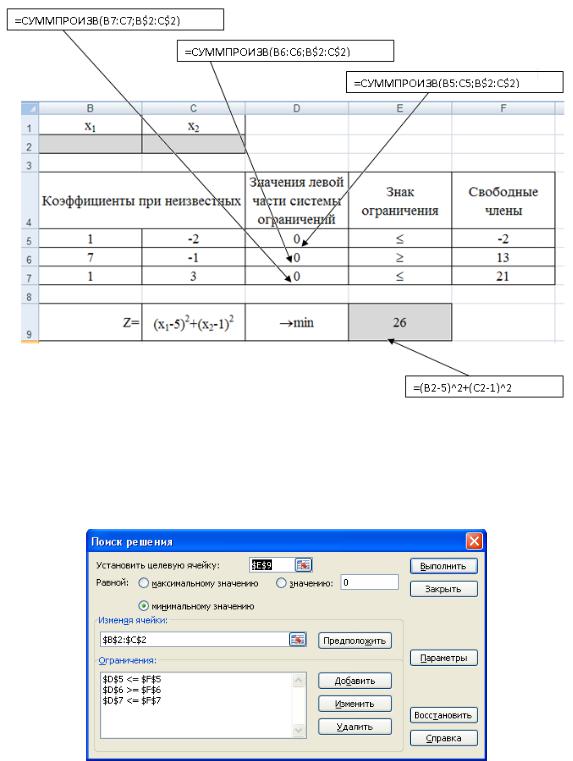
Рис. 51. Ввод формул для примера 20

Далее необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберите команду Поиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить в соответствии с рис. 52 (для добавления ограничений пользуемся кнопкой Добавить).

Рис. 52. Настройка «Поиска решений»

Далее нажимаем кнопку Параметры и в появившемся окне Параметры поиска решений устанавливаем флажок Неотрицательные значения и нажимаем OK (рис. 53).

84

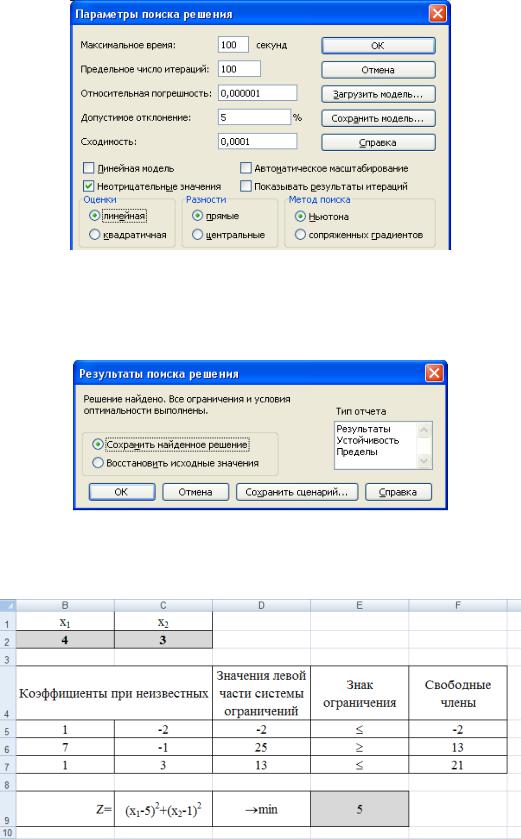
Рис. 53. Настройка параметров «Поиска решений»

В окне Поиск решения после нажатия кнопки Выполнить появляется окно Результаты поиска решения, в котором выбираем сохранение найденных значений и нажимаем кнопку ОК (рис. 54).

Рис. 54. Сохранение результатов «Поиска решений»

Результаты поиска решений (для ячеек В2 и С2 установлены числовые форматы с 0 знаками после запятой) приведены на рис. 55.

Рис. 55. Найденное оптимальное решение задачи примера 20

∙= 0,

Подставим в систему координаты оптимальной точки (4;3), найденной средствами Excel.

86

∙(21 −4 − 3∙3) = 0.

∙0 = 0, ∙12 = 0,∙8 = 0.

Произведение равно нулю, если один из множителей равен нулю. Из первого и второго уравнений следует, что выражения в скобках равны нулю. Из четвертого и пятого уравнений следует, что 2= 3=0. Подставим их в остальные

уравнения

2 − = 0, −4+2 = 0,

=0,

=0.

Откуда находим решение: 1=2, 2=0, 3=0. Следовательно, точка (4;3) является точкой экстремума.

Вопросы для самопроверки

1.В чем отличие НП от задачи ЗЛП?

2.В чем особенности нахождения решения задач НП?

3.Для каких задач НП разработаны методы решения?

4.В чем особенности графического решения задачи НП?

5.Какая функция называется функцией Лагранжа? Какой смысл множителей Лагранжа?

6.Сформулируйте условия Куна–Таккера.

7.Какие особенности имеет решение задачи выпуклого программирования?

87

ЛИТЕРАТУРА

1.Акулич И. Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1986. 319 с.

2.Интрилигатор М. Математические методы оптимизации и экономическая теория. М.: Айрис-Пресс, 2002. 553 с.

3.Исследование операций в экономике / Под ред. Н.Ш. Кремера. М.: ЮНИТИ, 2005. 407 с.

4.Конюховский П. В. Математические методы исследования операций в экономике. СПб: Питер, 2000. 208 с.

5.Косоруков О. А., Мищенко А. В. Исследование операций. М: Экзамен, 2003. 448 с.

6.Кузнецов А. В., Сакович В. А., Холод Н. И. Высшая математика. Математическое программирование. Минск: Вышэйшая школа, 1994. 286 с.

7.Кузнецов Ю. Н., Кузубов В. И., Волощенко А. Б. Математическое программирование. М.: Высшая школа, 1986. 302 с.

8.Эддоус М., Стэнсфилд Р. Методы принятия решений. М.: Аудит, ЮНИТИ, 1997. 590 с.

9.Шикин Е. В., Шикина Г. Е. Исследование операций. М.: ТК Велби, Про-

спект, 2006. 280 с.

88

Учебное издание

Галкина Марина Юрьевна

Методы оптимальных решений

Учебно-методическое пособие

Редактор Е.И. Ситняковская Корректор Н.А. Двуреченская

Подписано в печать 08.06.2016,

формат бумаги 60x84/16, отпечатано на ризографе, шрифт 10, п. л. 5,6, заказ № 99, тираж 10 экз.

Редакционно-издательский отдел СибГУТИ 630102, г. Новосибирск, ул. Кирова, 86, офис 105 тел. (383) 269-83-56

89