645_Galkina_M.JU._Metody_optimal'nykh_reshenij_

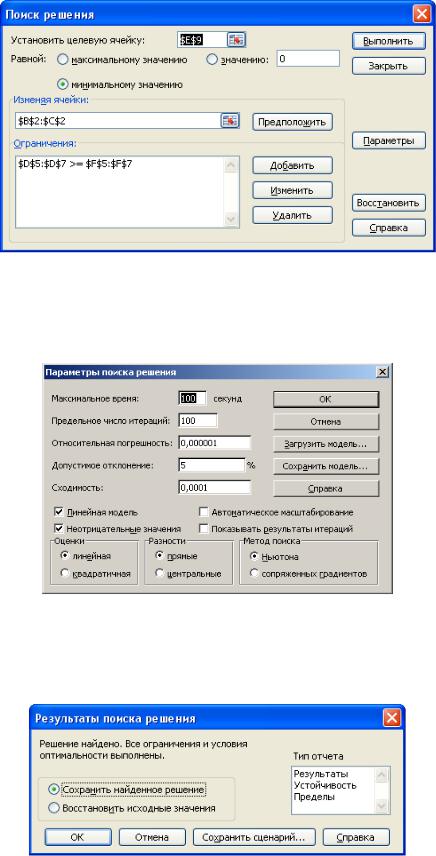
Рис. 12. Настройки Поиска решений для примера 4

Далее нажимаем кнопку Параметры и в появившемся окне Параметры поиска решений устанавливаем флажки Неотрицательные значения, Линей-

ная модель и нажимаем OK (рис.13).

Рис. 13. Настройки параметров Поиска решений для примера 4

В окне Поиск решения после нажатия кнопки Выполнить появляется окно Результаты поиска решения, в котором выбираем сохранение найденных значений и нажимаем кнопку ОК (рис.14).

Рис. 14. Сохранения результатов Поиска решений для примера 4

На рис. 15 представлены результаты поиска решений (для ячеек В2 и С2 установлены числовые форматы с нулевым количеством знаков после запятой).

21

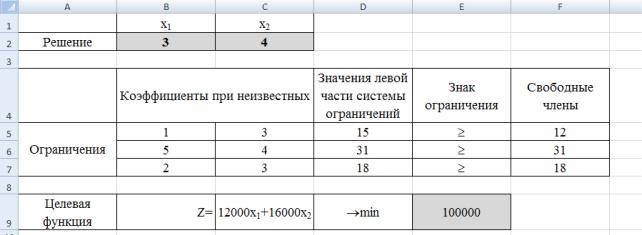
Рис. 15. Найденное решение в примере 4

Получили (3;4) = 100000. Решение совпадает с найденным графическим способом.

1.6.Двойственные задачи

Рассмотрим задачу использования сырья. Для изготовления двух видов продукции P1, P2 предприятие использует 4 вида сырья: S1, S2, S3, S4. Запасы сырья и расходы на изготовление каждого вида продукции приведены в таблице. Составить план производства, при котором стоимость выпущенной продукции будет максимальной.

Для составления математической модели задачи введем две переменные: x1 – количество произведенной продукции P1 и x2 – количество произведенной продукции P2. По определению эти переменные должны быть неотрицательны. При производстве продукции предприятие израсходует 2x1+3x2 единиц сырья S1, 2x1+x2 единиц сырья S2, 3x2 единиц сырья S3 и 4x2 единиц сырья S4. Предприятие не может израсходовать сырья больше, чем у него имеется, поэтому получаем следующие ограничения на использование имеющегося сырья:

3x1 2x2 20,

4x1 x2 16,

3x2 30,

4x1 40.

22

От продажи выпущенной продукции предприятие получит 10x1+6x2 у.е. Получаем математическую модель задачи:

3x1 2x2 20,

4x1 x2 16,

3x2 30,

4x1 40,

x1,x2 0,

Z(x1,x2) 10x1 6x2 max .

Предположим, что по некоторым обстоятельствам потребитель отказался от заказа и предприятие решило продать сырье, не выпуская продукцию. По каким ценам будет продаваться сырье? Составим математическую модель новой задачи.

Введем три переменные:

y1 стоимость единицы сырья S1, y2 стоимость единицы сырья S2, y3 стоимость единицы сырья S3, y4 стоимость единицы сырья S4.

По определению эти переменные должны быть неотрицательны. Предприятию имеет смысл не выпускать продукцию только в случае, если выручка от продажи сырья не меньше, чем стоимость произведенной из этого сырья продукции. На производство одной единицы продукции P1 расходуется 3 единицы сырья S1, 4 единицы сырья S2 и 4 единицы сырья S4. Если не выпускать продукцию P1, а продать все сырье, из которого его можно изготовить, то выручка от реализации этого сырья составит 3y1 4y2 4y4. Аналогично, выручка от реализации сырья, из которого можно изготовить продукцию P2, составит 2y1 y2 3y3. Выручка от продажи сырья должна быть не меньше стоимости единицы соответствующей продукции. Получаем ограничения:

3y1 4y2 4y4 10, 2y1 y2 3y3 6.

С другой стороны, покупатель сырья хочет купить это сырье как можно дешевле. На покупку сырья будет затрачено 20y1 16y2 30y3 40y4 у.е. Получаем математическую модель задачи:

3y1 4y2 4y4 10,

2y1 y2 3y3 6,

y1,y2,y3,y4 0,

W(y1,y2,y3, y4) 20y1 16y2 30y3 40y4 min.

Составленная задача называется двойственной к исходной. Как видно из построенных моделей, кроме экономической связи между ними существует и математическая связь. Перечислим условия, связывающие построенные задачи.

23

1.Количество переменных двойственной задачи соответствует количеству ограничений исходной задачи.

2.Цели задач противоположны: в исходной задаче функция максимизируется, а в двойственной – минимизируется.

3.Коэффициенты при неизвестных в целевой функции исходной задачи являются правыми частями в ограничениях двойственной задачи и, наоборот, правые части ограничений исходной задачи являются коэффициентами при неизвестных в целевой функции двойственной задачи.

4.Знаки неравенств задач противоположны: все неравенства исходной задачи имеют знак « », а двойственной – « ».

5.Матрица коэффициентов при неизвестных в системе ограничений двойственной задачи является транспонированной матрицей коэффициентов при неизвестных в системе ограничений исходной задачи.

6. Переменные обеих задач неотрицательны.

Заметим, что если к двойственной задаче построить двойственную, то получим исходную задачу. Поэтому говорят о паре симметричных взаимно двойственных задач.

Рассмотрим правила построения двойственной задачи в общем случае. Пусть имеется задачи линейного программирования в общем виде:

Каждой такой задаче можно поставить в соответствие двойственную задачу:

24

W b1y1 b2y2 bmym min.

Построение двойственной задачи происходит по следующим правилам:

1.Сначала производится согласование цели исходной задачи и неравенств

еесистемы ограничений. Если целевая функция максимизируется, то все знаки

неравенств должны быть « », если целевая функция минимизируется, то все знаки неравенств должны быть « ». Если какое-нибудь неравенство не соответствует цели задачи, то его следует домножить на -1 для смены знака на противоположный.

2.Каждому i-му ограничению системы исходной задачи соответствует переменная yi двойственной задачи и, наоборот, каждому j-му ограничению системы двойственной задачи соответствует переменная xi исходной задачи. Подпишем эти соответствия слева от систем.

3.Коэффициенты при неизвестных в целевой функции двойственной задачи совпадают с правыми частями системы ограничений исходной задачи.

4.Цель двойственной задачи противоположна цели исходной задачи.

5.Матрица системы ограничений двойственной задачи получается транспонированием из матрицы системы ограничений исходной задачи;

6.Коэффициенты правых частей двойственной задачи – это коэффициенты при неизвестных в целевой функции исходной задачи.

7.Знаки ограничений двойственной задачи могут быть либо неравенствами, соответствующими цели двойственной задачи, либо равенствами. Неравенство ставится в случае, если на переменную исходной задачи, соответствующую ограничению двойственной задачи, наложено условие неотрицательности. Если такого условия нет, то соответствующее ограничение двойственной задачи – уравнение.

8.На переменную yj двойственной задачи следует наложить условие неотрицательности лишь в том случае, если i-е ограничение исходной задачи – неравенство.

25

Пример 5

Построим двойственную задачу для следующей задачи.

x1 x2 x3 6,

2x1 x2 3x3 9,

3x1 x2 2x3 11,

x1,x3 0,

Z 5x1 4x2 6x3 max.

Согласуем знаки неравенств с целью задачи. Целевая функция максимизируется, поэтому все неравенства должны быть « ». Второе неравенство не согласовано с целью функции, умножим его обе части на -1.

x1 x2 x3 6,

2x1 x2 3x3 9,

3x1 x2 2x3 11,

x1,x3 0.

В системе имеется 3 ограничения, поэтому в двойственной задаче будет 3 переменные, подпишем эти переменные слева от ограничений.

y1 x1 x2 x3 6,

y2 2x1 x2 3x3 9,

y3 3x1 x2 2x3 11,

x1,x3 0.

Матрица левой части системы ограничений исходной задачи:

Матрица левой части системы ограничений двойственной задачи:

Двойственная задача: x1 y1 2y2 3y3 5,

x2 y1 y2 y3 4, x3 y1 3y2 2y3 6,

y1,y2 0,

W 6y1 9y2 11y3 min .

26

Второе ограничение является уравнением, т.к. на переменную x2 не наложено условие неотрицательности. На переменную y3 не наложено условие неотрицательности, т.к. соответствующее y3 ограничение исходной задачи – уравнение.

В силу того, что все три формы записи задачи линейного программирования (общая, симметричная, каноническая) эквиваленты, далее будем рассматривать пару симметричных двойственных задач.

Следующие теоремы дают зависимости между решениями пары двойственных задач.

дач в симметричной форме. Тогда W(Y) Z(X).

Экономический смысл Теоремы 5 заключается в том, что при любом допустимом плане производства общая стоимость всей произведенной продукции не превосходит суммарной оценки ресурсов, соответствующей любому допустимому решению двойственной задачи.

ных задач и W(Y*) Z(X*). Тогда X*, Y* – оптимальные решения этих задач. Экономический смысл Теоремы 6 заключается в том, что планы производ-

ства и оценки ресурсов оптимальны, если стоимость произведенной продукции совпадает с суммарной оценкой ресурсов.

Теорема 7 (О минимаксе) Если одна из пары двойственных задач имеет решение, то и другая имеет решение, причем Zmax Wmin . Если одна из пары двойственных задач имеет неограниченную функцию, то система ограничений второй задачи не совместна.

Экономический смысл Теоремы 7 заключается в том, что максимально возможная стоимость произведенной продукции совпадает с минимально возможной стоимостью сырья.

27

Теорема 8 (Равновесия) Пусть X* (x1*, ,xn*) и Y* (y1*, ,ym*) – допустимые планы пары двойственных задач в симметричной форме. Эти планы являются оптимальными тогда и только тогда, когда выполняются следующие условия дополняющей нежесткости:

Теорема 8 позволяет определить оптимальное решение одной из пары двойственных задач по решению другой. Если ограничение одной задачи при подстановке оптимального решения обращается в строгое неравенство, то соответствующая двойственная переменная в оптимальном решении двойственной задачи равна 0. Если в оптимальном плане одной задачи какая-нибудь переменная положительна, то соответствующее ей ограничение двойственной задачи является уравнением.

Дадим экономическую интерпретацию условиям дополняющей нежесткости. Если в оптимальном решении какое-нибудь сырье имеет отличную от 0 оценку, то оно будет израсходовано полностью (ресурс является дефицитным). Если сырье расходуется не полностью (находится в избытке), то его оценка равна 0. Таким образом, получаем, что двойственные оценки – это мера дефицитности сырья. Оценка показывает, на сколько возрастет значение целевой функции при увеличении запаса соответствующего сырья на 1 ед. Если некоторый вид продукции входит в план производства, то затраты на его производство совпадают со стоимостью произведенной продукции. Если затраты на производство какого-нибудь вида продукции больше стоимости продукции, то продукция не производится.

Вслучае если одна из пары двойственных задач содержит две переменных,

ееможно решить графически, а затем найти решение двойственной задачи, используя Теоремы 7 и 8. При этом могут возникнуть 3 случая: обе задачи имеют допустимые решения, допустимые решения имеет только одна задача, обе задачи не имеют допустимых решений.

28

Пример 6

Составить двойственную задачу и найти ее решение по теореме равнове-

сия.

x1 2y2 10,

x2 y1 2y2 9,

x3 2y1 2y2 19, x4 2y1 2y2 13,

x5 2y1 y2 11,y1,y2 0,

W 4y1 2y2 min .

Найдем оптимальное решение двойственной задачи по теореме равновесия. Запишем условия дополняющей нежесткости.

29

y1(4 (4 2 0 2 0 2 0)) 0,

y2( 2 (2 3 2 4 2 0 2 0 0)) 0,

3 (2y2 10) 0,

4 (y1 2y2 9) 0,0 ( 2y1 2y2 19) 0,

0 (2y1 2y2 13) 0,

0 ( 2y1 y2 11) 0.

Произведение равно нулю, если один из множителей равен 0. Получаем,

,≥ 0,

( , ) = 12000 +16000 → min.

В разделе 1.5 было найдено решение этой задачи средствами MS Excel:

(3;4) = 100 000.

Составим двойственную задачу. Знаки неравенств уже согласованы с це-

,≥ 0,

( , ) = 12000 +16000 → min.

30