645_Galkina_M.JU._Metody_optimal'nykh_reshenij_

Двойственная задача:

+5 +2 ≤ 12000,

3 +4 +3 ≤ 16000,

,, ≥ 0,

Вопросы для самопроверки

1.Может ли система ограничений общей ЗЛП включать строгие неравенства?

31

2.Может ли целевая функция ЗЛП содержать нелинейные выражения из переменных?

3.Может ли допустимое решение ЗЛП содержать отрицательную компоненту?

4.Чем отличается оптимальное решение ЗЛП от допустимого?

5.Чем отличается канонический вид ЗЛП от общего?

6.Каждая ли задача, заданная в симметричной форме, может быть приведена к канонической форме? Если да, то укажите, каким образом это делается?

7.Может ли задача, заданная в канонической форме, быть приведена к общему виду?

8.Какое максимальное число неравенств может содержать ЗЛП с двумя переменными?

9.Как строится область допустимых решений ЗЛП с двумя переменными?

10.Может ли область допустимых решений быть невыпуклым многоугольником?

11.Может ли область допустимых решений быть неограниченным множеством? Пустым?

12.Что такое градиент? Как его строить?

13.Что такое линия уровня? Как ее строить?

14.Может ли ЗЛП с двумя переменными иметь два и только два оптимальных решения?

15.В каком случае задача линейного программирования с двумя переменными не имеет решения?

16.Какой вывод можно делать из того, что область допустимых решений не ограничена по направлению, противоположному вектору целевой функции?

17.Сколько переменных может содержать ЗЛП, которую можно решить графически?

18.Можно ли для ЗЛП, содержащей в системе ограничений неравенства разных направлений, построить двойственную задачу?

19.Если в основной задаче отсутствуют условия неотрицательности переменных, то какие последствия это влечет в двойственной задаче?

20.Чем отличаются матрицы систем ограничений в паре двойственных задач?

21.Какова связь между оптимальными решениями пары двойственных задач?

22.Что можно сказать о решении двойственной задачи, если решение основной задачи не существует по причине несовместимости ее системы ограничений?

23.В чем смысл теоремы равновесия?

32

2. СПЕЦИАЛЬНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

2.1.Задача о назначениях

Пример 8

В каждом из пяти филиалов производственного объединения могут изготовляться изделия пяти видов. Учитывая необходимость углубления специализации, в каждом из филиалов решено выпускать только один вид продукции, при этом каждый из видов изделий должен выпускаться одним из филиалов. Себестоимость каждого изделия в каждом из филиалов различна и задается матрицей C ( – себестоимость производства i-м филиалом j-го вида продукции). Найти распределение выпуска продукции между филиалами, чтобы общая себестоимость выпущенной продукции была минимальной.

=0,иначе,

i= 1,2,3,4,5, j = 1,2,3,4,5.

Каждый филиал должен выпускать только один вид продукции:

Каждая вид продукции должен выпускаться:

x11 x21 x31 x41 x51 1,

x12 x22 x32 x42 x52 1,

x13 x23 x33 x43 x53 1,

Условие неотрицательности переменных:

xij 0, i = 1,2,3,4,5, j = 1,2,3,4,5.

Суммарная себестоимость выпущенной продукции:

33

Z 5x11 11x12 6x13 11x14 4x15 10x21 11x22 9x23 11x24 5x25 7x318x32 6x33 8x34 2x35 6x41 4x42 3x43 7x44 8x45 4x51 2x52 5x54

8x55 min.

Подобную задачу можно решать симплекс-методом, но можно использовать специальный метод – венгерский. Алгоритм венгерского метода:

1этап

1.В каждой строке находим минимальный элемент и вычитаем его из всех элементов соответствующей строки.

2.В каждом столбце находим минимальный элемент и вычитаем его из всех элементов соответствующего столбца.

2этап

1. Проводим минимальное количество вертикальных и горизонтальных линий, пересекающих все нули.

2. Если количество таких линий равно количеству строк матрицы С, то 2-ой этап завершен.

3. В противном случае выберем среди неперечеркнутых элементов минимальный и построим новую матрицу по правилам:

а) из неперечеркнутых элементов вычитаем минимальный элемент; б) к элементам, через которые проведены две линии, прибавляем минимальный элемент; в) все остальные элементы не меняем.

Далее переходим на п.3 текущего этапа.

3этап

Впостроении решения участвует последняя матрица из этапа 2.

1. Находим строку или столбец матрицы, в которой имеется единственный 0. Если такой строки или столбца нет, то берем любую строку или столбец, содержащие нули. Пусть = 0.

2.Тогда в матрице X = 1 и все остальные элементы i-ой строки и j-го столбца равны 0.

3.В матрице С вычеркиваем i-ю строку и j-ый столбец.

4.Если в матрице С остался один элемент, то соответствующий элемент матрицы X равен 1 и этап 3 закончен. Иначе переходим на п.1 текущего этапа. Решим сформулированную выше задачу.

34

элементы 5-ой строки и 3-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 5-ю строку и 3-ий столбец.

3.Среди оставшихся невычеркнутыми элементов матрицы С второй столбец содержит единственный 0 (c42=0). Поэтому считаем, что x42=1, а все остальные элементы 4-ой строки и 2-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 4-ю строку и 2-ой столбец.

4.Среди оставшихся невычеркнутыми элементов матрицы С нет строк или столбцов, содержащих единственный 0. Поэтому выбираем любой нулевой элемент (например, c24=0) и считаем, что x24=1, а все остальные элементы 2- ой строки и 4-го столбца матрицы X равны 0. В матрице С исключаем из дальнейшего рассмотрения 2-ю строку и 4-ый столбец.

5. Т.к. c35=0, то x35=1.

Итак, оптимальное решение задачи о назначениях:

Zmin= 5 + 11 + 2 + 4 + 0 = 22.

Решим задачу о назначениях с использованием средств MS Excel.

Для решения нашей задачи создадим в Excel книгу с именем «Решение задачи о назначениях». Подготовим данные на листе (рис. 16).

36

Сначала определим ячейки, в которые будут вводиться элементы матрицы С. Пусть это будут ячейки B3:F7. Заполним их и оформим заголовки строк и столбцов. Определим ячейки, куда будет помещен результат решения. Пусть это будут ячейки B12:F17, сделаем у них заголовки. В этих ячейках нет данных, их должен будет рассчитать Excel, они выделены цветом. Заведем строку 18 для целевой функции. Цветом выделена ячейка, в которой будет находиться значение целевой функции для найденного оптимального решения.

Рис. 16. Подготовка данных для примера 8

В ячейки G12:G16 введем нахождение сумм неизвестных по строкам, в ячейки B17:F17 – нахождение сумм неизвестных по столбцам, в ячейку D18 – формулу для нахождения целевой функции (рис.17).

37

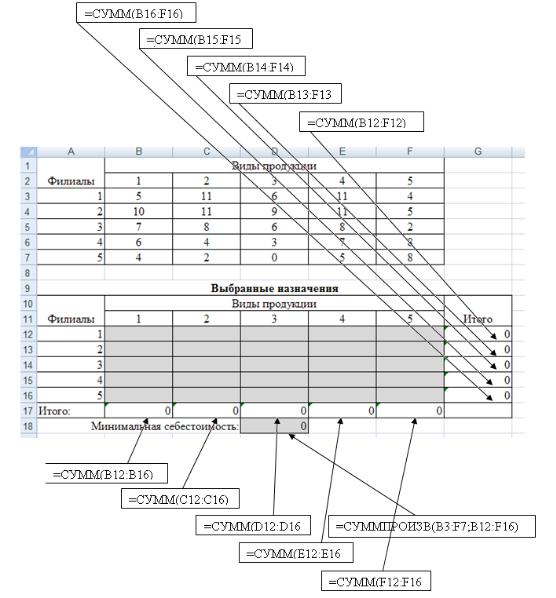
Рис. 17. Ввод формул для примера 8

Далее необходимо воспользоваться надстройкой Поиск решения. На вкладке Данные в группе Анализ выберите команду Поиск решения. Появится диалоговое окно Поиск решения, которое необходимо заполнить следующим образом (для добавления ограничений пользуемся кнопкой Добавить) (рис.18).

38

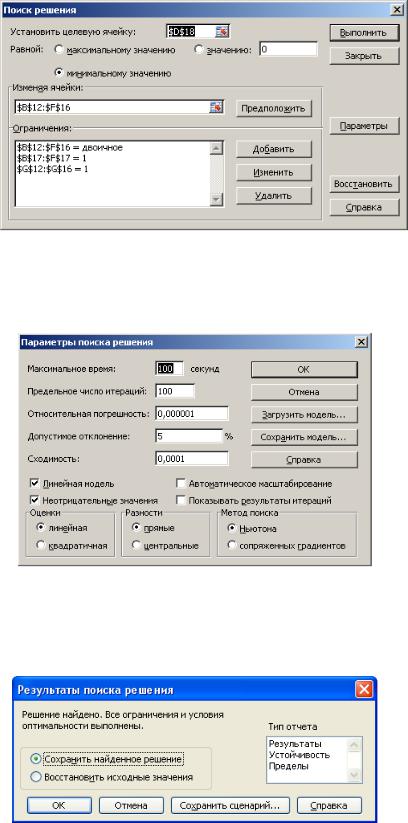
Рис. 18. Настройки Поиска решений для примера 8

Далее нажимаем кнопку Параметры и в появившемся окне Параметры поиска решений устанавливаем флажок Неотрицательные значения, Линейная модель и нажимаем OK (рис.19).

Рис. 19. Настройки параметров Поиска решений для примера 8

В окне Поиск решения после нажатия кнопки Выполнить появляется окно Результаты поиска решения, в котором выбираем сохранение найденных значений и нажимаем кнопку ОК (рис.20).

Рис.20. Сохранение результатов Поиска решений для примера 8

На рис. 21 представлены результаты поиска решений.

39

Рис. 21. Найденное оптимальное решение для примера 8

ным венгерским методом. Интерпретация решения:

Первый филиал должен выпускать 1-ый вид изделий, второй филиал должен выпускать 4-ый вид изделий, третий филиал должен выпускать 5-ый вид изделий, четвертый филиал должен выпускать 2-ой вид изделий, пятый филиал должен выпускать 3-ий вид изделий. При таком распределении себестоимость выпуска изделий будет минимальна и составит 22 у.е.

Алгоритм решения задачи о назначениях предполагает минимизацию ее целевой функции. Если имеется задача о назначениях, целевую функцию которой нужно максимизировать, то поступают таким же образом, как и при переходе от одной формы записи к другой в задаче линейного программирования: все элементы матрицы умножаются на (- 1) и далее решают, как в случае минимизации.

Если матрица С не является квадратной, в нее следует включить дополнительные фиктивные строки и столбцы, необходимые для приведения ее к квадратной форме. Значения стоимости, соответствующие фиктивным клеткам, как правило, равны нулю. Назначения, размещаемые в клетках фиктивных строк, фактически не существуют. Назначения, соответствующие фиктивным столб-

40