
Обработка данных в среде MATLAB
.pdf
Матрица |
f2 |
|
|
|
|
3.174 |
0.17 |
0.63; |
3.662 |
0.24 |
0.83; |
2.686 |
0.19 |
0.71; |
3.662 |
0.22 |
0.85; |
3.174 |
0.10 |
0.42; |
3.906 |
0.22 |
0.81; |
2.686 |
0.19 |
0.73; |
3.906 |
0.22 |
0.85; |
2.686 |
0.21 |
0.77; |
3.906 |
0.24 |
0.88; |
2.441 |
0.22 |
0.87; |
3.906 |
0.24 |
0.84; |
2.930 |
0.23 |
0.83; |
3.906 |
0.22 |
0.86; |
2.930 |
0.23 |
0.85; |
3.906 |
0.23 |
0.85; |
3.418 |
0.22 |
0.84; |
3.906 |
0.23 |
0.81; |
3.174 |
0.20 |
0.84; |
4.150 |
0.22 |
0.87; |
3.418 |
0.22 |
0.80; |
3.906 |
0.11 |
0.61 |
Содержание отчета
1.Название, цель и задачи работы.
2.Тексты программ и изображения графических окон, которые требовалось сохранять в ходе выполнения работы.
3.Объяснение полученных результатов и выводы.
5.МЕТОД ЛИНЕЙНОЙ ДИСКРИМИНАНТНОЙ ФУНКЦИИ ФИШЕРА (ПРИВЕДЕНИЕ ДАННЫХ К ОДНОМЕРНОМУ ВИДУ)
Цели работы: знакомство с методом линейной дискриминантной функции Фишера (приведение данных к одномерному виду) в случае двух классов; получение навыков работы с этим методом в системе MATLAB.
Основные положения
Для двух классовой задачи линейная дискриминантная функция (ЛДФ) или разделяющая гиперплоскость, которая определяет алгоритм распознавания, имеет вид:
D(x) WтX a 0 или WтX a ,
где W – весовой вектор единичной длины; a – скалярная пороговая величина. Алгоритм распознавания в этом случае имеет вид:
если WтX |
a , то |
1 (1-й класс), |
если WтX |
a , то |
2 (2-й класс). |
Чтобы определить ЛДФ, надо найти W и a. Один из возможных путей решения этой задачи заключается в выполнении следующего алгоритма.
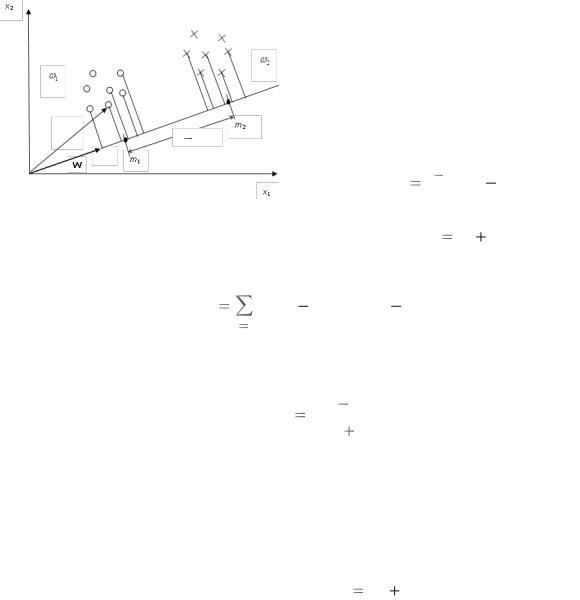
1. Найти W как наилучшее положение этого вектора в n-мерном пространстве, для которого проекции точек классов на направление W разделены наилучшим образом.
21
|
|
2. Спроектировать точки обоих классов на прямую, определяемую поло- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жением W (рис. 5.1). |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Решить одномерную задачу по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поиску наилучшей величины а, например |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щ2 |
|||
|
|
щ1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
по критерию минимума ошибок класси- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фикации. |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Решение 1-го шага определяется вы- |
||||
|
|
x |
|
|
|
|
|
|
|
m |
|
||||||
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
m1 |
m2 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
y11 |
|
1 |
|
|
|
|
|
|
ражением |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
||||
|
|
|
|
|
W |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W SW1(M1 |
M2) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
||
|
|
|
|
|
|
Рис. 5.1 |
|
|
|
|
|
|
где M1 и M2 – векторы средних значений |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двух классов; SW S1 |
S2 – усредненная |
матрица разброса для двух классов;
nj |
т |
S j Xi( j) M j Xi( j) M j |
i1
–матрица разброса для j-го класса (аналог корреляционной матрицы). Опре-
деленный таким образом весовой вектор дает максимум критерия Фишера
J (W) |
(m1 |
m2)2 |
, |
|
s2 |
s2 |
|||
|
|
|||
|
1 |
2 |
|
где s12 и s22 – выборочный разброс классов, т. е. максимальное отношение разброса между классами к «среднему» разбросу внутри классов. Для W, найденного по данному критерию, классы, спроектированные на направление W, максимально удалены друг от друга.
В практических расчетах вместо матрицы SW можно использовать усредненную ковариационную матрицу У У1 У2 .
Анализ данных с помощью ЛДФ Фишера в системе MATLAB
Пример 5.1
Пусть даны 2 массива данных (f1 и f2 из работы 4).
По этим данным надо найти оптимальный весовой вектор по критерию максимума расстояния Фишера (найти ЛДФ Фишера), спроектировать классы на этот весовой вектор, построить гистограммы для обоих классов и эмпирически найти оптимальный порог по критерию минимума ошибок классификации. Эту задачу можно решить с помощью следующей программы.
load ('f1.txt') % загрузка матрицы 1-го класса load ('f2.txt') % загрузка матрицы 2-го класса
A1=f1
22

X |
|
|
12 |
|
|
|
|
|
|
|
A2=f2 |
|
|
|
|
|
|
|
|
|
|
n1=length(A1) % число членов |
10 |
|
|
|
|
|
|
|
||
|
|
щ2 |
|
|
|
|
|
|
|
|
% 1-го класса |
|
|
|
|
|
|
|
|
||
щ1 |
|
|
8 |
|
|
|
|
|
|
|
n2=length(A2) % число членов |
|
|
|
|
|
|
|
|||
% 2-го класса |
|
|
|
|
|
|
|
|
|
|
m1= mean(A1) |
m2 |
6 |
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
m2= mean(A2) |
m1 m2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
|
|
|
E1=n1*cov(A1)y m |
|
|
|
|
|
|
|
|
||
W |
1 |
1 |
|
|
|
|
|
|
|
|
E2=n2*cov(A2) |
X1 |
2 |
|
|
|
|
|
|
|
|
E=E1+E2 |
|
|
|
|
|
|
|
|
|
|
W=inv(E)*(m1-m2)' |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
w=W/norm(W) |
% нормализация |
|
|
|
|
Рис. 5.2 |
|
|
|
|
% весового вектора |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
X1=A1*w |
% множество проекций |
|
|
|
|
|
|
|
|
|
%векторов 1-го класса на w |
|
|
|
|
|
|
|
|
||
X2=A2*w % множество проекций векторов 2-го класса на w |
|
|
||||||||
t=-0.3:0.05:0 |
|
|
|
|
|
|
|
|
|
|
x1=hist(X1,t) |
|
|
|
|
|
|
|
|
|
|
x2=hist(X2,t) |
|
|
|
|
|
|
|
|
|
|
plot(x1) |
|
|
|
|
|
|
|
|
|
|
hold on |
|
|
|
|
|
|
|
|
|
|
plot(x2)% минимальное число ошибок равно 3=1+2 |
|
|
|
|||||||
Результат расчетов представлен на рис. 5.2. |
|
|
|
|
|
|
||||
Задание
1.Провести анализ данных по ирисам Фишера с использованием ЛДФ Фишера.
2.Используя все 4 признака, найти оптимальный весовой вектор при
рассмотрении только двух классов: setosa и virginica.
3. Сформулировать алгоритм классификации и оценить получаемые ошибки.
Порядок выполнения работы
1.С использованием всех признаков найти оптимальный весовой вектор по критерию максимума расстояния Фишера.
2.Спроектировать классы на этот весовой вектор, построить гистограммы и эмпирически найти оптимальный порог по критерию минимума ошибок классификации.
3.Сформулировать полученный алгоритм классификации. Привести полученные ошибки.
23

Содержание отчета
1.Название, цель и задачи работы.
2.Тексты программ и изображения графических окон, которые требовалось сохранять в ходе выполнения работы.
3.Объяснение полученных результатов и выводы.
6. АВТОМАТИЧЕСКАЯ КЛАССИФИКАЦИЯ
Цели работы: исследование методов автоматической классификации, основанных на теории статистических решений; получение навыков работы с линейными и квадратичными решающими правилами в системе MATLAB.
Основные положения
Для целей распознавания классов (классификации) в n-мерном пространстве каждому классу сопоставляется своя дискриминантная функция, которая может быть линейной или нелинейной, например, квадратичной. Линейная дискриминантная функция ЛДФ имеет вид
D X WтX a |
n |
|
w x |
w , |
|
|
k k |
n 1 |
k |
1 |
|
где X – входной вектор; W – весовой вектор; |
a – пороговая величина. Для |
|
области объектов данного класса его дискриминантная функция наибольшая. Поверхность, разделяющая две смежные области, определяется равенством двух соответствующих ЛДФ, т. е.
|
n |
Di(X) Dj(X) |
wk xk wn 1 0, |
|
k 1 |
где wk wik wjk , wn 1 wi(n 1) |
wj(n 1) . |
Полученное уравнение – это уравнение гиперплоскости в n-мерном признаковом пространстве. Рассмотрим методы определения коэффициентов уравнений, основанные на теории статистических решений. Предполагается, что классы взяты из генеральной совокупности, распределенной по нормальному закону, поэтому определяющими параметрами для классов являются векторы средних значений и ковариационные матрицы. В простейшем случае ковариационные матрицы считаются равными. Оценку такой матрицы можно получить, усредняя все ковариационные матрицы классов.
Реализация автоматической классификации в системе MATLAB
Автоматическая классификация в системе МАТЛАБ осуществляется с помощью функции classify в виде
24
class = classify(sample,training,group) class = classify(sample,training,group,type)
class = classify(sample,training,group) классифицирует каждую
строку данных в выборочной матрице sample на одну из групп, представленных в обучающей матрице training. sample и training должны быть матрицами с одинаковым числом столбцов. group это группирующая переменная для матрицы training. Ее однозначно определяемые значения определяют группы, каждый элемент определяет ту группу, к которой принадлежит соответствующая строка матрицы training. group может быть категориальной переменной (переменной, определенной на шкале наименований), числовым вектором, строковым массивом или строковой матрицей. Матрицы training и group должны иметь одинаковое число строк. Выход class указывает группу, к которой приписывается каждая строка матрицы sample и имеет тот же тип, что и group.
class = classify(sample,training,group,type) позволяет опреде-
лить желаемый вид дискриминантной функции. type может быть одним из следующих:
'linear' – Подгоняет многомерную нормальную плотность к каждой группе с оценкой объединенной ковариационной матрицы. Этот тип используется по умолчанию.
'quadratic' – Подгоняет многомерные нормальные плотности с оценками ковариаций отдельно по каждой группе.
Пример 6.1 (рис. 6.1)
% Используем массив a из примера 1.1.
Проведем линейную классификацию для 3 классов по первому признаку матрицы a.
linclass = classify(a(:,1),a(:,1),g) bad = ~strcmp(linclass,g)
numobs = size(a,1) sum(bad) / numobs
ans =
0.3600
Проведем линейную классификацию для классов A, B, C по 1-му и 2-му признакам:
linclass = classify(a(:,1:2),a(:,1:2),g) % линейная
%классификация
bad = ~strcmp(linclass,g) % формирование вектора ошибок
25

2-й признак
Обучение и классификация на статистических данных
8
|
Класс |
A |
7 |
Класс |
B |
|
|
|
|
Класс |
C |
6 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
00 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
1-й признак |
|
|
|
||
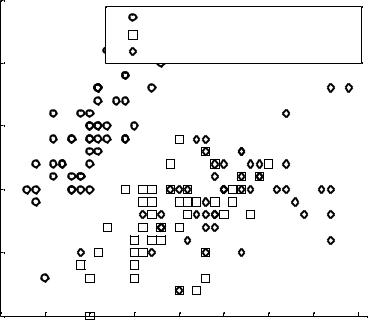
Рис. 6.1
numobs = size(a,1)
sum(bad) / numobs % средняя ошибка классификации
ans =
0.3000
Из 30 объектов 30 %, или 10 объектов, классифицированы неправильно посредством линейной дискриминантной функции.
% Построим групповую диаграмму рассеяния gscatter для %исходных данных: классы A,B,C по 1-му и 2-му признакам.
gscatter(a(:,1),a(:,2),g,'','xos') % групповая диаграмма
% рассеяния для классов A,B,C по 1-му и 2-му признакам. xlabel('1-й признак');
ylabel('2-й признак');
legend('Класс A','Класс B','Класс C','Location','NW') title('{\bf Обучение и классификация на статистических данных}')
hold on
Теперь, наложив знак «+» на неверно классифицированные точки, можно увидеть ошибки классификации.
plot(a(bad,1), a(bad,2), 'k+'); hold off;
26
Пример 6.2 (рис. 6.2)
Исследуем, как измерения чашелистика (его длина – sepal length и ширина – sepal width) различаются между видами. Будем использовать только два столбца, содержащие измерения чашелистика.
load fisheriris
gscatter(meas(:,1), meas(:,2), species,'rgb','osd'); xlabel('Длина чашелистика')
ylabel('Ширина чашелистика')
legend('Ирисы щетинистые (setosa)','Ирисы разноцветные
(versicolor)','Ирисы виргинские
(virginica)','Location','NE')
title('{\bf Классификация обучающих данных по ирисам Фише-
ра}')
Классифицируем эти данные, используя стандартный линейный метод.
linclass = classify(meas(:,1:2),meas(:,1:2),species); bad = ~strcmp(linclass,species);
numobs = size(meas,1); sum(bad) / numobs
ans =
0.2000 |
|
|
|
|
|
|
|
|
|
|
Классификация обучающих данных по ирисам Фишера |
||||||||
|
4.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ирисы щетинистые (setosa) |
||||
чашелистика |
|
|
|
|
Ирисы разноцветные (versicolor) |
||||
4 |
|
|
|
Ирисы виргинские (virginica) |
|||||
|
|
|
|
|
|
|
|
||
3.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ширина |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
24 |
4.5 |
5 |
5.5 |
6 |
6.5 |
7 |
7.5 |
8 |
|
|
|
|
Длина чашелистика |
|
|
|||
Рис. 6.2
27
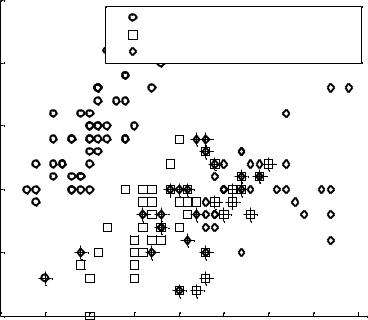
Из 150 образцов 20 %, или 30 образцов, классифицированы ошибочно с помощью линейной дискриминантной функции. Наложив знак «+» на неверно классифицированные точки, можно посмотреть, что это за образцы (рис. 6.3).
hold on;
plot(meas(bad,1), meas(bad,2), 'k+'); hold off;
Дискриминантная функция разделила «линиями» плоскость рис. 6.3 на |
|||||||||
области и присвоила различным областям принадлежность различным видам. |
|||||||||
|
Классификация обучающих данных по ирисам Фишера |
||||||||
|
4.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ирисы щетинистые (setosa) |
||||
чашелистика |
|
|
|
|
Ирисы разноцветные (versicolor) |
||||
4 |
|
|
|
Ирисы виргинские (virginica) |
|||||
|
|
|
|
|
|
|
|
||
3.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ширина |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
24 |
4.5 |
5 |
5.5 |
6 |
6.5 |
7 |
7.5 |
8 |
|
|
|
|
Длина чашелистика |
|
|
|||
Рис. 6.3
Как линейный, так и квадратичный дискриминантный анализ предназначены для ситуаций, для которых измерения по каждой группе имеют многомерное нормальное распределение. Часто это разумное допущение, но иногда делать такое допущение нежелательно или ясно видно, что оно недействительно.
Задание
1.Исследовать применение функции classify (линейный и квадратичный варианты) к классам A, B, C из примера 1.1.
2.Исследовать применение функции classify (линейный и квадратичный варианты) к трем классам ирисов Фишера.
28
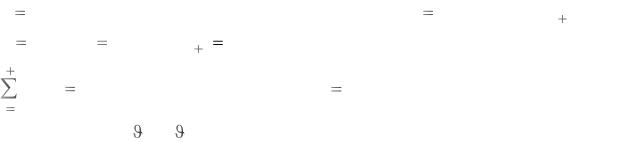
3.Оценить ошибки классификации во всех случаях и сравнить их с ошибками, полученными на занятиях.
4.Сделать вывод о важности числа признаков и вида решающей функции на качество классификации.
Порядок выполнения работы
1.Провести линейную классификацию массива а из примера 1.1 на классы A, B, C по всем 4 признакам. Оценить ошибки классификации.
2.Провести квадратичную классификацию массива а из примера 1.1 на классы A, B, C по всем 4 признакам. Оценить ошибки классификации.
3.Провести линейную классификацию ирисов Фишера на 3 класса по всем 4 признакам. Оценить ошибки классификации.
4.Провести квадратичную классификацию ирисов Фишера на 3 класса по всем 4 признакам. Оценить ошибки классификации.
Содержание отчета
1.Название, цель и задачи работы.
2.Тексты программ и изображения графических окон, которые требовалось сохранять в ходе выполнения работы.
3.Объяснение полученных результатов и выводы.
7.НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ КЛАССИФИКАЦИИ
Цели работы: знакомство с непараметрическими методами классификации для случая 2 классов; получение навыков работы с этим методом в си-
стеме MATLAB.
|
|
|
|
|
|
Основные положения |
|
Для |
непараметрических методов классификации входные векторы |
||||
X |
(x1, x2, ..., xn) |
представляются в виде векторов Y (y1, y2, ..., yn, yn 1) , где |
||||
yi |
xi для i 1, ..., n, |
yn 1 1. Тогда разделяющая граница приобретает вид |
||||
n 1 |
0 или в векторном виде WтY 0. Для двух линейно непересека- |
|||||
|
wk yk |
|||||
k |
1 |
|
|
|
|
|
ющихся классов |
1 |
и |
2 |
можно найти такой весовой вектор W, для которого |
||
|
|
|
|
|
||
выполняется требование:
29

|
WтY |
0 для каждого Y |
1, |
|
|
WтY |
0 для каждого Y |
2 . |
|
|
Если все объекты второго класса умножить на –1, то для целей обуче- |
|||
ния |
вышеприведенное условие |
приобретает вид: WтY 0 для каждого |
||
Y |
( 1 |
2) . |
|
|
Рассмотрим процедуру последовательного обучения, когда обучающие объекты Y предъявляются последовательно, по одному, а весовой вектор W уточняется с каждым новым входным вектором Y. В этом случае если после
предъявления объекта Y |
выполняется WтY 0 , то W остается неизмен- |
ным. Если же WтY 0 , |
то вычисляется новое значение W, равное W', по |
формуле |
|
|
W W cY , |
где c > 0 называется коэффициентом коррекции. Объекты предъявляются либо циклически, либо в случайном порядке до тех пор, пока не повторится результат испытания каждого из них. Начальное значение W произвольно (но не равно нулю).
Анализ данных с помощью непараметрических методов классификации в системе MATLAB
Реализация вышеприведенного алгоритма последовательного обучения в системе МАТЛАБ может быть проиллюстрирована на следующем примере.
Пример 7.1
Пусть даны 2 массива данных: class_1 и class_2.
class_1 |
|
class_2 |
|
||
0.4 |
0.9 |
0.6; |
0.6 |
0.3 |
1.0; |
0.6 |
0.6 |
1.2; |
0.4 |
0.4 |
1.2; |
0.8 |
0.3 |
1.2; |
0.6 |
0.5 |
0.7; |
0.6 |
0.5 |
1.0; |
0.5 |
0.5 |
0.8; |
0.5 |
0.6 |
1.1; |
0.3 |
0.2 |
0.6; |
0.5 |
0.7 |
1.0; |
0.2 |
0.2 |
0.7; |
0.7 |
0.3 |
1.2; |
0.4 |
0.2 |
0.8; |
0.6 |
0.6 |
1.5; |
0.8 |
0.3 |
0.6; |
0.7 |
0.7 |
1.0; |
0.5 |
0.6 |
0.4; |
0.4 |
1.0 |
0.4 |
0.9 |
0.3 |
0.5 |
По этим данным надо провести процедуру обучения и найти оптимальный весовой вектор по критерию отсутствия ошибок распознавания. Эту за-
30
