
Обработка данных в среде MATLAB
.pdf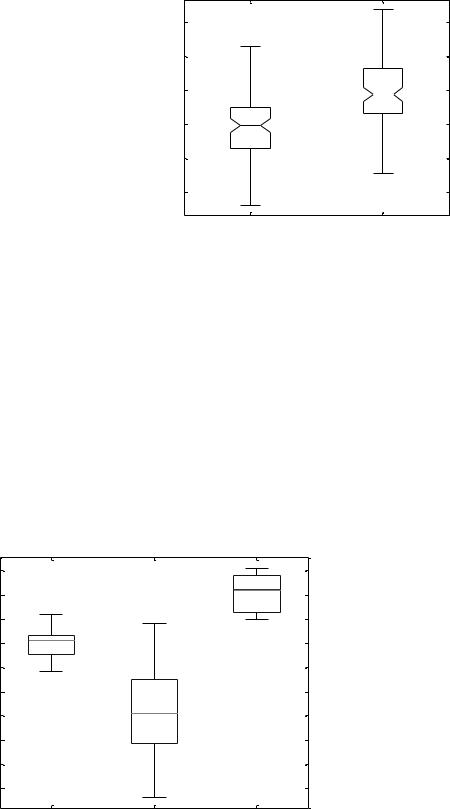
Риски отстоят от коробочек на наиболее экстремальное значение в препределах whis*iqr, где whis – значение параметра 'whisker', а iqr – межквартильный размах данной выборки.
Пример 2.3
Данный пример показывает boxplots с зазубринами для двух групп выборочных данных (рис. 2.5).
88
77
66
Values 55
44
33
1
R = normrnd(MU,SIGMA,m,n) вы-
дает значения (здесь – 100 шт.) нор-
мального распределения со средним MU, дисперсией SIGMA. ность m × n, где m – число строк, а n – число столбцов.
x1 = normrnd(5,1,100,1);
x2 = normrnd(6,1,100,1); boxplot([x1,x2],'notch','on')
22
R имеет размер-
Разница между медианами этих двух групп составляет примерно 1. Так как зазубрины на этих коробочках не перекрываются, можно заключить, что со значимостью 95 % истинные медианы различаются.
Пример 2.4
Используя массив a из примера 1.1, построим boxplot для 1-го признака по 3 классам: A, B, C (рис. 2.6).
Values
8
7
6
5
4
3
2
1
0
–-11
+
A B C
Рис. 2.6
gg=['A'; 'A'; 'A'; 'A'; 'A'; 'A'; 'A'; 'A'; 'A'; 'A'; 'B'; 'B'; 'B'; 'B'; 'B'; 'B'; 'B'; 'B'; 'B'; 'B'; 'C';'C'; 'C'; 'C'; 'C'; 'C'; 'C'; 'C'; 'C'; 'C']
11

7
6.5
6
5.5
Values
5
4.5
4
3.5
3
%gg – символьная матрица g=cellstr(gg)
%cellstr – функция преобразующая символьную матрицу в
%матрицу строк
%g – матрица элементов (строк); ее размерность равна 30х1;
%первые 10 строк матрицы g равны ‘A’, вторые – ‘B’, третьи –
%‘C’
boxplot(a(:,1),g)
|
|
|
|
|
|
|
Пример 2.5 |
|
|
|
|
|
|
|
В этом примере сравнивается дли- |
|
|
|
|
|
|
|
на лепестков в выборках двух видов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ирисов (рис. 2.7): |
|
|
|
|
|
|
load fisheriris |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
s1 = meas(51:100,3); |
versicolor |
virginica |
||||||
Рис. 2.7 |
s2 = meas(101:150,3); |
|
|
|
boxplot([s1 s2],'notch','on', |
'labels',{'versicolor','virginica'}) |
|
Данный график имеет следующие свойства:
Верх и низ каждой «коробочки» – это 25-й и 75-й процентили данной выборки соответственно. Расстояния между верхушками и нижними гранями – это межквартильные диапазоны.
Линия в середине каждой коробочки – это медиана выборки. Если медиана не находится в центре коробочки, она указывает на асимметрию выборки.
Риски это линии, находящиеся над и под каждой коробочкой. Риски наносятся от концов межквартильных диапазонов до наиболее дальних наблюдений в пределах рисочной длины (регулируемые значения).
Наблюдения за пределами рисочной длины маркируются как выбросы. По умолчанию, выброс это значение, которое больше 1.5 межквартильного диапазона от верхушки или низа коробочки, но эта величина может регулироваться с помощью дополнительных входных аргументов. Выбросы отображаются с помощью красного значка «+».
Зазубрины показывают вариабильность медианы между выборками. Ширина зазубрины вычисляется, поэтому те коробочки, чьи зазубрины не перекрываются (как изображено выше) имеют различные медианы при уровне значимости 5 %. Уровень значимости основан на допущении нормальности распределений, но сравнение медиан достаточно робастно и для других распределений. Сравнение boxplot-медиан похоже на визуальную проверку гипотез, аналогичную t-тесту, используемому для средних.
12
Задание
1.Освоить методы графического вывода групп одномерных данных с помощью функций hist и boxplot.
2.Освоить методы сравнение групп одномерных данных.
3.Оценить различия групп одномерных данных с помощью функций
hist и boxplot.
Порядок выполнения работы
1.Запустите систему MATLAB.
2.Постройте диаграммы hist и plot по 3-му признаку (длина лепестка) для двух классов ирисов Фишера: setosa и versicolor.
3.Постройте диаграмму boxplot по 2-му признаку (ширина чашелистика) для двух классов ирисов Фишера: setosa и versicolor.
4.Создайте 2 массива (для каждой бригады – своих) из 10 случайных чисел каждый по нормальному закону с параметрами из табл. 2.2.
Таблица 2.2
Массив |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
V9 |
|
V10 |
|
1 |
m = 2 |
m = 3 |
m = 4 |
m = 5 |
m = 6 |
m = 3 |
m = 5 |
m = 6 |
m = 7 |
m = 8 |
|
|
σ = 1 |
σ = 1 |
σ = 1 |
σ = 2 |
σ = 2 |
σ = 2 |
σ = 1 |
σ = 1 |
σ = 2 |
σ = 3 |
|
||
|
|
|||||||||||
2 |
m = 6 |
m = 8 |
m = 7 |
m = 2 |
m = 2 |
m = 7 |
m = 2 |
m = 7 |
m = 3 |
m = 4 |
|
|
σ = 2 |
σ = 4 |
σ = 3 |
σ = 1 |
σ = 1 |
σ = 4 |
σ = 1 |
σ = 1 |
σ = 2 |
σ = 2 |
|
||
|
|
|||||||||||
5. Для полученных массивов постройте диаграмму boxplot |
с зазубри- |
|||||||||||
нами. Дайте анализ различия между этими массивами.
Содержание отчета
1.Название, цель и задачи работы.
2.Тексты программ и изображения графических окон, которые требовалось сохранять в ходе выполнения работы.
3.Объяснение полученных результатов и выводы.
3. СРАВНЕНИЕ ДВУМЕРНЫХ ДАННЫХ
Цели работы: получение навыков работы по отображению двумерных данных в системе MATLAB.
13
Основные положения
Диаграмма рассеяния scatter
Для визуального отображения одной группы двумерных данных на плоскости используется функция scatter(x,y). Она отображает кружочки (маркеры) в местах расположения, заданных векторами x и y (которые должны быть одного и того же размера). scatter(x,y) рисует маркеры, имеющие размер и цвет по умолчанию. С помощью дополнительных параметров можно задавать различные типы, размеры и цвета маркеров.
Диаграмма рассеяния по группам gscatter
Для целей визуального сравнения данных нескольких групп объектов по 2 признакам используется диаграмма рассеяния по группам (функция gscatter). Она определяется следующим образом.
gscatter(x,y,group) создает график рассеяния на плоскости двух переменных x и y, отображаемых по группам. x и y являются векторами одинакового размера. group – это переменная группировки в виде строкового массива. Точки одной группы отображаются на графике одинаковыми маркерами и цветом.
gscatter(x,y,group,clr,sym,siz) также как и в функции plot назна-
чает цвет, тип и размер маркера для каждой группы. clr это строковый массив цветов (по умолчанию 'bgrcmyk') sym это строковый массив типа маркера (по умолчанию '.'. siz – это вектор размеров маркеров.
|
4.5 |
|
|
|
|
чашелистикаШирина |
|
|
|
|
setosa |
|
|
|
|
признакй-2 |
|
|
|
|
|
|
versicolor |
|
4 |
|
|
|
virginica |
|
3.5 |
|
|
|
|
|
3 |
|
|
|
|
|
2.5 |
|
|
|
|
|
24 |
5 |
6 |
7 |
8 |
|
|
|
Длина чашелистика |
|
|
|
|
Рис. 3.1 |
|
|
|
|
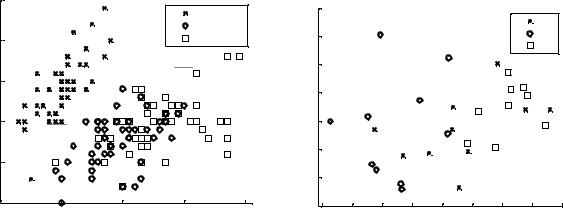
Пример 3.1 (рис. 3.1) |
|
|
||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
8 |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
7 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
1-й признак |
|
|
|
|
|
Рис. 3.2
load fisheriris gscatter(meas(:,1),meas(:,2),species,'','xos')
14
Пример 3.2 (рис. 3.2)
Используя массив a из примера 1.1, построим gscatter для 3 классов: A, B, C по 1-му и 2-му признакам.
gscatter(a(:,1),a(:,2),g,'','xos')
Задание
1.Освоить методы графического вывода групп двухмерных данных с помощью функции gscatter.
2.Изучить методы сравнение групп двухмерных данных.
Порядок выполнения работы
1. Загрузите данные по ирисам Фишера.
2. Отобразите в пространстве двух признаков: 3-го (длина лепестка) и 4-го (ширина лепестка) все три класса ирисов.
3. Создайте 2 группы (класса) двумерных данных, состоящих из 10 отсчетов каждая. Данные – это векторы, каждый из которых состоит из 2 компонент. Компоненты векторов представляют собой выборку случайных чисел из нормального закона с параметрами, указанными в таблице.
Номер группы |
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
||||||
(класса) |
Пр. 1 |
Пр. 2 |
Пр. 1 |
Пр. 2 |
Пр. 1 |
Пр. 2 |
Пр. 1 |
Пр. 2 |
Пр. 1 |
Пр. 2 |
|
1 |
m=2 |
m=7 |
m=3 |
m=5 |
m=4 |
m=6 |
m=8 |
m=5 |
m=3 |
m=6 |
|
σ=1 |
σ=2 |
σ=1 |
σ=2 |
σ=1 |
σ=2 |
σ=3 |
σ=1 |
σ=2 |
σ=1 |
||
|
|||||||||||
2 |
m=6 |
m=3 |
m=8 |
m=2 |
m=7 |
m=2 |
m=4 |
m=2 |
m=7 |
m=7 |
|
σ=2 |
σ=2 |
σ=4 |
σ=1 |
σ=3 |
σ=1 |
σ=2 |
σ=1 |
σ=4 |
σ=1 |
||
|
|||||||||||
4. Отобразите в пространстве полученных двух признаков данные классы. Сделайте вывод о сходстве ваших классов.
Содержание отчета
1.Название, цель и задачи работы.
2.Тексты программ, которые требовалось сохранять в ходе выполнения работы.
3.Объяснение полученных результатов и выводы.
4. МЕТОД ГЛАВНЫХ КОМПОНЕНТ (ПРИВЕДЕНИЕ ДАННЫХ К ДВУМЕРНОМУ ВИДУ)
Цели работы: получение навыков работы с методом главных компонент в системе MATLAB; вычисление главных компонент для биомедицинских данных.
15

Основные положения
Часто исходное число р рассматриваемых, т. е. измеряемых на исследуемых объектах, признаков довольно велико. Для визуализации картины, простоты интерпретации и упрощения счета очень часто необходимо представить каждое из наблюдений в виде набора чисел, состоящего из существенно меньшего (чем р ) числа признаков. При этом оставшиеся признаки могут либо выбираться из числа исходных, либо определяться по какому-либо правилу по совокупности исходных признаков, например как линейные комбинации последних
Главные компоненты представляют собой новое множество исследуемых признаков
y(1), y(2), , y( p) ,
каждый из которых получен в результате некоторой линейной комбинации, непосредственно измеренных на объектах, исходных признаков x(1), x(2), , x( p) . Полученные в результате такого преобразования новые признаки y(1), y(2), , y( p) могут обладать рядом удобных статистических свойств. Например, быть упорядоченными по степени рассеяния в изучаемой совокупности объектов: первый признак обладает наибольшей степенью рассея-
ния, т. е. наибольшей дисперсией, второй – меньшей и т. д.
Определение главных компонент
Будем предполагать, что исследуемые наблюдения X1, X2, , Xn извлечены из некоторой р -мерной генеральной совокупности, определяемой соответствующей вероятностной мерой. Однако для приводимых здесь понятий из всех характеристик исследуемой генеральной совокупности суще-
ственное значение имеет лишь ковариационная матрица |
ij , где |
|||
ij |
M x(i) |
a(i) |
x( j) a( j) , i, j 1, 2, |
, p . |
|
|
|
|
|
Здесь a(i) – компоненты вектора a средних значений признаков x(i) . Будем считать, что вектор средних значений a = 0, чего всегда можно добиться, рас-
сматривая в качестве исходных признаков x(1), x(2), , x( p) не сами измерения, а их отклонения от своих выборочных средних значений.
16

Назовем первой главной компонентой исследуемой генеральной совокупности наблюдений такую нормированную линейную комбинацию р ис-
ходных признаков x(1), |
x(2), |
, x( p) , |
|
|
|
|
|
|
||||
|
|
|
y(1) |
l11x(1) |
l12x(2) |
|
l1p x( p) |
Lт1X |
|
|
|
|
(здесь Lт |
l |
l |
l |
|
, причем l2 |
l2 |
l2 |
1), которая среди всех |
||||
1 |
11 |
12 |
1p |
|
11 |
12 |
1p |
|
|
|
|
|
прочих нормированных линейных комбинаций x(1), x(2), |
, x( p) |
обладает |
||||||||||
наибольшей дисперсией. |
|
|
|
|
|
|
|
|
||||
Вообще, i-й главной компонентой исследуемой генеральной совокуп- |
||||||||||||
ности (i |
2, 3, , р) будем называть такую нормированную линейную ком- |
|||||||||||
бинацию p исходных признаков x(1), x(2), |
, x( p) |
|
|
|
|
|||||||
|
|
|
y(i) |
|
li1x(1) |
li2x(2) |
|
lipx( p) |
Lтi X , |
|
|
|
которая среди всех прочих линейных нормированных (l2 |
l2 |
l2 |
1) |
|||||||||
|
|
|
|
|
|
|
|
|
i1 |
i2 |
ip |
|
комбинаций, некоррелированных со всеми предшествующими главными
компонентами |
y(1), |
, |
y(i 1) (т. е. |
cov y(i), y( j) |
M y(i) y( j) |
0 для j |
i ), |
||||||||||
обладает наибольшей дисперсией. |
|
|
|
|
|
|
|
|
|||||||||
Из |
определения |
следует, |
что, во-первых, главные |
компоненты |
|||||||||||||
y(1), y(2), |
|
, y( p) занумерованы в |
порядке убывания их дисперсий, т. |
е. |
|||||||||||||
Dy(1) Dy(2) |
Dy( p) , причем легко подсчитать, что, во-первых, |
|
|||||||||||||||
|
|
|
|
|
Dy(i) |
M Lтi X 2 |
M LтiXXтLi |
Lтi |
Li |
|
|
|
|||||
и, во-вторых, |
вектор |
Li , |
определяющий преобразование |
перехода |
от |
||||||||||||
x(1), x(2), |
|
, x( p) к y(i) , является так называемым i -м собственным вектором ко- |
|||||||||||||||
вариационной матрицы |
, т. е. его компоненты li1, |
li2, |
, |
lip |
определяются |
||||||||||||
|
|
|
|
|
|
p |
l2 |
|
|
|
|
|
|
|
|
|
|
как нормированное ( |
|
1) решение системы уравнений |
|
|
|
||||||||||||
|
|
|
|
|
|
|
i j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iI Li |
0 , |
|
|
|
|
|
|
где i – i-й по величине корень уравнения |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
I |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Под |
|
M |
|
подразумевается определитель матрицы М, под I – единичная |
|||||||||||||
|
|
||||||||||||||||
матрица, а под – неизвестное число. |
|
|
|
|
|
|
|||||||||||
Из вышеприведенных выражений вытекает, что Dy(i) |
i. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|

Таким |
образом, ковариационная |
матрица |
Y |
главных |
компонент |
|||
|
|
|
|
|
|
|
|
|
y(1), y(2), |
, y( p) будет иметь вид |
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
0 |
0 |
. |
|
|
|
|
|
|
|
|
|
||
|
Y |
. |
. . . |
. |
|
|
||
|
|
|
|
|||||
|
|
|
|
|
||||
|
|
0 |
0 |
0 |
p |
|
|
|
|
|
|
|
|
|
|
|
|
Опираясь на то, что преобразование, с помощью которого осуществляет- |
||||||||
ся переход от исходных компонент X к главным компонентам Y, |
(Y = LX) , |
|||||||
ортогональное, нетрудно выразить исходные переменные |
x(1), x(2), |
, x( p) |
||
через главные компоненты |
x(i) l1i y(1) l2i y(2) |
lpi y( p) |
(в матричной запи- |
|
си X = LтY ), а также |
показать, что сумма |
дисперсий (Dy(1) Dy(2) |
||
Dy( p)) главных компонент равна сумме дисперсий |
(Dx(1) Dx(2) |
+ |
||
Dx( p)) исходных признаков. |
|
|
|
|
Анализ главных компонент в системе MATLAB
Анализ главных компонент (Principal components analysis – PCA) в систе-
ме MATLAB осуществляется с помощью функции princomp(X) в виде:
PC = princomp(X) или [PC,SCORE,latent,tsquare] = princomp(X)
Функция PC = princomp(X) предназначена для проведения анализа главных компонент многомерной случайной величины Х. Входной параметр Х является матрицей (n × p) исходных данных. Столбцы матрицы Х соответствуют признакам, строки – наблюдениям многомерной случайной величины. Функция возвращает матрицу главных компонент PC (p × p), где p – число признаков многомерной случайной величины, или число столбцов матрицы Х. Каждый столбец матрицы PC содержит коэффициенты одной главной компоненты. Столбцы расположены в порядке убывания дисперсии компонент. Матрица PC является множеством собственных векторов ковариационной матрицы cov(Х). В процессе своей работы princomp центрирует X путем вычитания среднего значения из колонок, но не меняет шкалу X.
Функция [PC, SCORE, latent, tsquare] = princomp(X) возвращает
матрицу главных компонент PC, матрицу оценок SCORE, которая является проекцией X в пространство главных компонент. Строки матрицы SCORE соответствуют наблюдениям, а столбцы – компонентам. Кроме того эта функция возвращает
18
latent – вектор, содержащий собственные значения ковариационной матрицы X и tsquare – вектор значений статистики T2 Хоттелинга для каждого из наблюдений. Значения вектора latent являются дисперсиями столбцов SCORE. Статистика T2 Хоттелинга это мера многомерного расстояния каждого наблюдения от центра множества данных. Элементы latent, tsquare могут отсутствовать.
С помощью функции PC = pcacov(Y) можно найти главные компоненты с помощью ковариационной матрицы Y исходных данных.
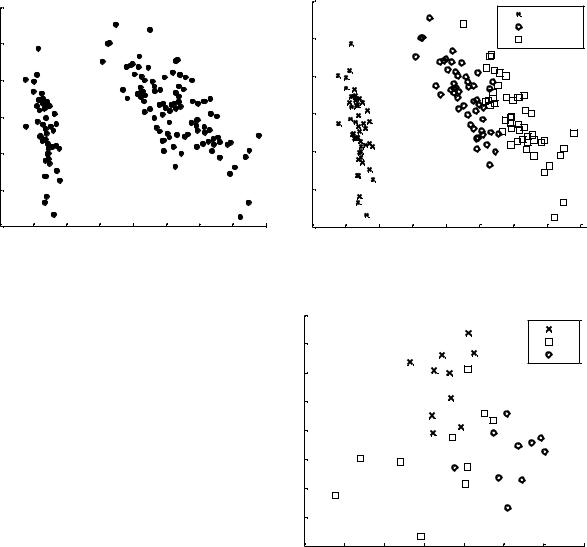
Пример 4.1 (рис. 4.1)
Построить в пространстве двух первых главных компонент изображение всех трех классов ирисов Фишера.
Главная компонента 2
1.5
1
0.5
0
-0.5
-1
-1.5 |
|
|
|
|
|
|
|
|
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
Главная компонента 1
Главная компонента 2
1.5
|
setosa |
|
versicolor |
1 |
virginica |
|
0.5
0
-0.5
-1
-1.5 |
|
|
|
|
|
|
|
|
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
Главная компонента 1
Рис. 4.1
load fisheriris [PC,SCORE] = princomp(meas)
scatter(SCORE(:,1),SCORE(:,2))
Пример 4.2 (рис. 4.2)
Построить в пространстве двух первых главных компонент изображение всех трех классов ирисов Фишера с маркировкой классов (с помощью переменной группировки species):
load fisheriris [PC,SCORE] = princomp(meas)
gscatter(SCORE(:,1),SCORE(:, 2), species,'','xos')
Рис. 4.2
компонента |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
C |
|
2 |
|
|
|
|
|
|
|
главная |
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-я |
-1 |
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
-8 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
1-я главная компонента
Рис. 4.3
19
Пример 4.3 (рис. 4.3)
Используя массив a из примера 1.1, построим gscatter для классов A, B, C по двум первым главным компонентам. Для этого надо (как в примере 1.1) построить матрицу a, переменную группировки g и далее использовать функцию
[PC,SCORE] = princomp(a).
[PC,SCORE] = princomp(a)
gscatter(SCORE(:,1), SCORE(:, 2), g,'','xos')
Задание
1.Ознакомиться с теоретическими положениями метода главных ком-
понент.
2.Освоить использование функции princomp на биологических и статистических данных.
3.Освоить отображение данных в пространстве двух главных компонент
спомощью функций scatter и gscatter.
Порядок выполнения работы
1.Ввести в компьютер две матрицы данных f1 и f2 для двух классов A и B.
2.Вычислить переменную группировки g, как это было сделано в примере 1.1.
3.Вычислить главные компоненты для объединенной матрицы [f1; f2]
ив пространстве двух первых главных компонент отобразить полученные данные с использованием функции gscatter и переменной группировки g.
4.Сделать вывод о возможности линейного разделения классов и оценить получаемые ошибки.
Матрица |
f1 |
|
|
|
|
|
0.997 |
0.05 |
0.15; |
2.686 |
0.19 |
0.80; |
|
2.930 |
0.15 |
0.54; |
||||
0.997 |
0.09 |
0.28; |
||||
2.93 |
0.13 |
0.72; |
||||
1.221 |
0.09 |
0.40; |
||||
1.221 |
0.11 |
0.56; |
||||
0.997 |
0.10 |
0.39; |
||||
1.953 |
0.19 |
0.72; |
||||
0.997 |
0.10 |
0.40; |
||||
0.997 |
0.13 |
0.53; |
||||
1.709 |
0.13 |
0.72; |
||||
1.221 |
0.12 |
0.41; |
||||
1.953 |
0.22 |
0.91; |
||||
1.221 |
0.07 |
0.29; |
||||
1.221 |
0.07 |
0.28; |
||||
0.997 |
0.11 |
0.51 |
||||
2.441 |
0.17 |
0.76; |
||||
|
|
|
20
