Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ploskost_i_pryamaya_v_prostranstve

.pdf

Скачиваний:

Добавлен:

09.02.2015

Размер:

437.27 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

а плоскость общим уравнением

P : Ax + By + Cz + D = 0 .

1) Угол между прямой и плоскостью равен углу между направляющим вектором s (l, m, n) прямой и нормальным вектором N ( A, B,C) плоскости и

вычисляется по формуле

sinϕ =

Al + Bm + Cn

(3.1)

+ B2 + C 2 ×

l 2 + m2 + n2

2) Условие параллельности прямой и плоскости имеет вид

Al + Bm + Cn = 0 .

(3.2)

Оно равносильно условию ортогональности векторов N и s

(N ^ s ).

3) Условие перпендикулярности прямой и плоскости имеет вид

(3.3)

m n

Оно равносильно условию коллинеарности векторов N и s

(N || s ) .

4) Условие принадлежности прямой L плоскости P записывается в виде

Al + Bm + Cn = 0,

(L || P),

Ax + By

+ Cz

+ D = 0,

P),

(3.4)

где x0 , y0 , z0 − координаты точки M 0 , принадлежащей прямой.

3.2. Решение типовых задач

x − 3

y − 6

z + 7

Задача 27. Найти острый угол между прямой

- 2

плоскостью 4x − 2 y − 2z − 3 = 0 .

Решение. Направляющий вектор прямой равен s (1, 1, − 2) . Нормальный

вектор плоскости равен N (4, -2, -2) . По формуле (3.1)

sinϕ =

Al + Bm + Cn

4 ×1 - 2 ×

- 2 × (-2)

ϕ = π .

+ B2 + C2 × l 2 + m2 + n2

1 +1 + 4 16 + 4 + 4 2

Ответ: ϕ = π . 6

Задача 28. При каком значении C прямая L : 3x − 2 y + z + 3 = 0,

4x − 3y + 4z + 1 = 0

параллельна плоскости P : 2x − y + Cz − 2 = 0 ?

Решение. Согласно условию задачи прямая L задана как линия пересе-

чения двух плоскостей. Нормальный

вектор

первой плоскости

равен

N1 (3, - 2, 1) , нормальный вектор второй плоскости равен N2 (4,

- 3,

4) . На-

= N1 ´ N2 (см. формулу (2.8)):

правляющий вектор прямой равен s

-2 1

s =

= -5i - 8 j - k .

-3

это условие ортого-

Условие параллельности прямой L и плоскости P

нальности направляющего

вектора

прямой s (-5, - 8,

-1) и нормального

вектора плоскости N (2, -1,

= 0 . Умножая,

получаем

C) , т.е. N × s

2 × (-5) + (-1) × (-8) + C(-1) = 0 ,

или C = -2 .

Таким образом, уравнение плоскости будет 2x - y - 2z - 2 = 0 .

Ответ: C = -2.

x − 3

y − 3

Задача 29. При каких значениях C и D прямая

лежит в

- 3

плоскости 2x - y + Cz + D = 0 ?

Решение. Прямая будет параллельна плоскости, если ее направляющий

вектор s (2,

- 3, 7)

будет

ортогонален

нормальному

вектору

плоскости

N (2, -1, C) . Запишем это условие N × s = 0 :

2 × 2 -1× (-3) + 7C = 0,

откуда

C = -1.

Прямая

будет

принадлежать

плоскости,

если

координаты

точки

M 0 (3, 3, 0) , через которую проходит прямая, удовлетворяют уравнению плоскости: M 0 P . Отсюда получаем, что 2 × 3 - 3 -1× 0 + D = 0, или D = -3.

При решении задачи мы воспользовались формулой (3.4).

Ответ: C = -1, D = -3.

Задача 30. Найти точку пересечения прямой L : x − 6 = y − 5 = z + 6 и
1	3	- 4

плоскости P : x + 3y - 4z + 7 = 0.

Решение. Запишем уравнения прямой в параметрическом виде

x = 6 + t,y = 5 + 3t,

z = -6 - 4t.

Подставляя выражения для x, y, z в уравнение плоскости P , получим

6 + t1 + 15 + 9t1 + 24 + 16t1 + 7 = 0, или 26t1 = −52, t1 = −2.

Теперь следует подставить значение параметра t1 = −2 в параметрические уравнения прямой L . Находим x1 = 4, y1 = −1, z1 = 2 .

Ответ: M1 (4, − 1, 2).

∙ Полезная формула.

Если прямая L :

x = x0 + lt,

y = y0 + mt, z = z0 + nt

пересекается с плоскостью P : Ax + By + Cz + D = 0 , то точке пересечения

M1 отвечает значение параметра t1 , равное

t1 = −

Ax0 + By0 + Cz0 + D

(3.5)

Al + Bm

+ Cn

Задача 31. Найти уравнение плоскости P , проходящей через прямую

L :

x − 6

y −1

z − 4

перпендикулярно плоскости P : x + y − z + 1 = 0.

Решение. Плоскость

имеет два

направ-

ляющих вектора

s (2, 1, 1) и

N2 (1, 1, −1)

и про-

ходит через точку M 0 (6, 1, 4) . Согласно форму-

ле (1.9) её уравнение будет иметь вид

x − 6

y −1 z − 4

= 0 , или

−1

−2(x − 6) + 3( y −1) + (z − 4) = 0 .

Окончательно 2x − 3y − z − 5 = 0 .

Ответ: 2x − 3y − z − 5 = 0 .

Задача 32. Известны координаты вершин тетраэдра: A1 (0, 1, 2);

A2 (4, 3, 5); A3 (5, 0, 4); A4 (3, 2, 3) . Найти уравнение и длину его высоты A4 A5 .

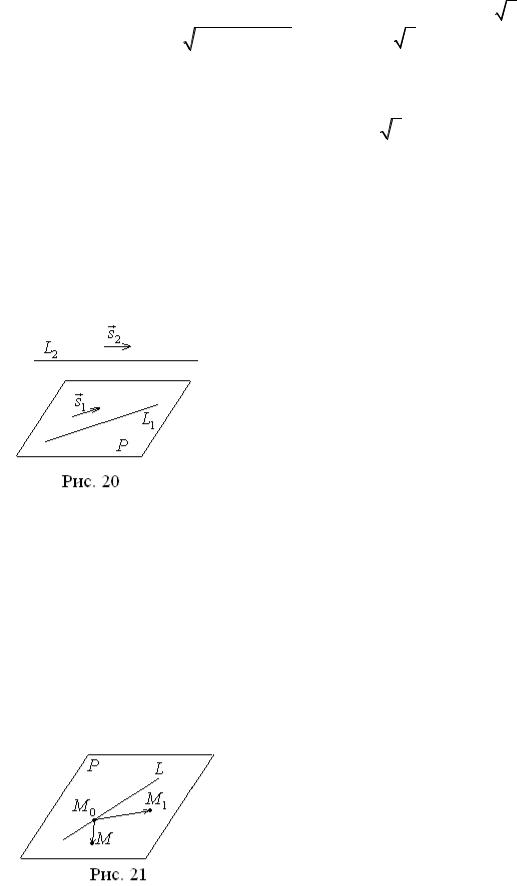
Решение. Данный тетраэдр мы рассматривали в

задаче 10. Уравнение основания A1 A2 A3 имеет вид x + y − 2z + 3 = 0 . В качестве направляющего вектора s

высоты A4 A5 можно выбрать нормальный вектор грани

R	= N (1, 1,	− 2) . Кроме того, нам известны
A1 A2 A3 , т. е. s

координаты точки A4 (3, 2, 3) , через которую проходит высота. Воспользуемся каноническими уравнениями

прямой (2.3). Тогда получим A A :		x − 3	=	y − 2	=	z − 3	.

4	5	1	1			−2

Высоту h можно найти по формуле (1.7), определяющей расстояние от точки

A4 (3, 2, 3) до грани A1 A2 A3 : x + y − 2z + 3 = 0 .

Ax4 + By4 + Cz4

+ D

1×3 +1× 2 - 2 ×3 + 3

h =

+ B2 + C 2

Напоминаем, что A, B, C, D – это коэффициенты в общем уравнении плос-

кости x + y − 2z + 3 = 0 , и они равны A = 1, B = 1, C = −2, D = 3.

x − 3

y − 2

z − 3

Ответ: A A

;

h =

-2

Задача 33. Даны прямые L :

x − 6

y −1

z − 4

x + 1

y − 2

z + 7

−1

−7

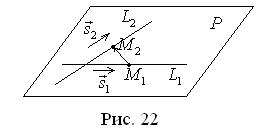
Найти уравнение плоскости P, проходящей через прямую L1 параллельно

прямойL2 .

(2, 1, 1)

(1,

− 1,

− 7) являются направляющими

Решение. Векторы s1

и s2

векторами плоскости P . Точка M1 (6, 1, 4)

принад-

лежит плоскости P . Решаем задачу, используя

формулу (1.9):

x - 6

y -1 z - 4

= 0 ,

или

-1

-7

−6(x − 6) + 15( y −1) − 3(z − 4) = 0 .

Окончательно 6x −15 y + 3z − 39 = 0 .

Ответ: 6x −15 y + 3z − 39 = 0 .

Задача 34. Составить уравнение плоскости, проходящей через прямую

L :

x + 1

y −1

z + 2

и точку M1

(3, 0, 2) .

-3

M 0 (−1, 1, − 2)

Решение. Прямая L проходит через точку

и ее направ-

ляющий вектор равен s (4, − 3, 1) . Произвольная

точка M (x, y,z) будет при-

надлежать искомой плоскости P ,

если векторы M 0 M , M 0 M1

и s компла-

нарны:

, т. е.

M 0 M × M 0 M1 ´ s = 0

x - x0

y - y0

z - z0

x1 - x0

y1 - y0

z1 - z0

= 0 .

Это и есть уравнение плоскости P . Подставляем

координаты и вычисляем определитель разложением по элементам первой строки. Получаем

x + 1

y −1

z + 2

−1

= 0 ,

11(x + 1) + 12( y −1) − 8(z + 2) = 0 .

−3

Окончательно 11x + 12 y − 8z −17 = 0 .

Ответ: 11x + 12 y − 8z −17 = 0 .

∙ Полезная формула. Уравнение плоскости, проходящей через прямую

L :

x − x0

y − y0

z − z0

и точку M

(x , y , z ) , не лежащую на этой прямой,

имеет вид

x − x0

y − y0

z − z0

x1 − x0

y1 − y0

z1 − z0

= 0

(3.6)

Задача 35. Доказать, что прямые L :

x −1

y + 2

z −3

x + 2

y +1

z + 2

L :

лежат в одной плоскости и найти уравнение этой

−2

плоскости.

Решение. Первая прямая проходит че-

рез точку M1 (1,

− 2, 3)

и ее направляющий

(1, 2, 4)

. Вторая прямая проходит

вектор s1

через точку M 2 (−2,

−1,

− 2) и ее направ-

− 2, 4)

. Очевидно,

что прямые лежат в одной плоско-

ляющий вектор

s2 (3,

сти, если векторы M1M

компланарны:

2 , s1 ,

M1M 2 × s1

´ s2 = 0 , т. е.

x2 − x1

y2 − y1

z 2 −z1

= 0 .

Подставим заданные координаты:

−3

−1

= 0 .

−2

R R

Это означает, что прямые L1 и L2 лежат в одной плоскости. Векторы s1 и s2

не коллинеарны. Следовательно, эти прямые пересекаются.

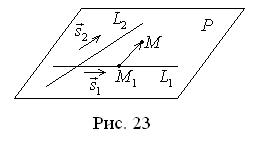
Найдем уравнение плоскости P , в которой лежат прямые L1 и L2 . Оче-

видно, что произвольная точка M (x, y,z) будет принадлежать плоскости,

если векторы M1M , s1 , s2 компланарны:

R		R	= 0	, т. е.
M1M × s1	´ s2		= 0	, т. е.
		x − x1		y − y1	z − z1	= 0 .
		x − x1		y − y1	z − z1
			l1	m1	n1
			l2	m2	n2

Это и есть уравнение искомой плоскости. Подставляем координаты и вычисляем определитель разложением по элементам первой строки.

Получаем

x −1

y + 2

z − 3

= 0 ,

16(x −1) + 8( y + 2) − 8(z − 3) = 0 .

или

−2

Окончательно

2x + y − z + 3 = 0 .

Ответ: 2x + y − z + 3 = 0 .

∙ Полезные формулы. Две прямые

x − x2

y − y2

z − z2

L1 :

x − x1

y − y1

z − z1

и L2 :

лежат в одной плоскости, если

x2 − x1

y2 − y1

z 2 −z1

= 0 .

(3.7)

Если прямые пересекаются, то уравнение этой плоскости будет

x − x1

y − y1

z − z1

= 0 .

(3.8)

Замечание. Прямые

скрещиваются (т. е. не лежат в одной плоскости)

¹ 0 и формула (3.7) не имеет места.

тогда и только тогда, когда M1M 2 × s1

´ s2

Задача 36. Найти уравнение плоскости, проходящей через две парал-

лельные прямые:

L :

x − 2

y + 1

z − 3

L :

x −1

y − 2

z + 3

−2

Решение. Направляющие векторы этих
прямых	равны s1 = s2 = s(3, 2, − 2) .	Первая
прямая проходит через точку M1 (2,		−1, 3) ,
вторая	через точкуM 2 (1, 2, − 3) .	Произ-

вольная точка M (x, y, z) принадлежит иско-

мой плоскости

P , если

векторы

M1M ,

M1M 2 и s

компланарны:

= 0 ,

т. е.

M1M × M1M 2 ´ s

x − x1

y − y1

z − z1

x2 − x1

y2 − y1

z2 − z1

= 0 .

Подставляя заданные координаты, находим уравнение плоскости P.

x − 2

y + 1

z − 3

или 6(x − 2) − 20( y + 1) −11(z − 3) = 0 .

−1

−6

= 0 ,

−2

Окончательно

6x − 20 y −11z + 1 = 0 .

Ответ: 6x − 20 y −11z + 1 = 0 .

∙ Полезная формула. Уравнение плоскости, проходящей через две па-

( L1 ||

L2 ,

раллельные прямые

= s2

= s )

L :

x − x1

y − y1

z − z1

x − x2

y − y2

z − z2

, имеет вид

x − x1

y − y1

z − z1

x2 − x1

y2 − y1

z2 − z1

= 0 .

(3.9)

Замечание. В задачах 3, 9, 31, 34, 35, 36 без труда можно указать два направляющих вектора искомых плоскостей. Поэтому решение этих задач аналогично решению задачи 2. Если эти направляющие векторы явно не обозначены в ходе решения, то найдите их самостоятельно.

Задача 37. Найти координаты проек-

ции M 1	точки	M 0 (1, 2, −1) на плоскость
P : 3x − y + 2z − 27 = 0 .
Решение.		Находим	параметрические
уравнения прямой L , проходящей через
точку	M 0 (1,	2, −1)	перпендикулярно
плоскости P .		В качестве направляющего

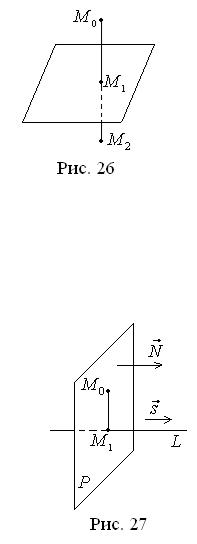
вектора s прямой L можно выбрать нормальный вектор N плоскости P ,

т.е. положить	R	= N (3,	−1, 2) . Параметрические уравнения прямой L будут
	s

(см. формулу (2.2)):

x = 1 + 3t,y = 2 − t,

z = −1 + 2t.

По формуле (3.5) находим значение параметра t = t1 , при котором прямая пересекает плоскость. Получим t1 = −2 . Подставим это значение в парамет-

рические уравнения прямой и вычислим координаты точки M1 :

x1 = 7, y1 = 0, z1 = 3.

Ответ: M1

(7, 0, 3).

Задача 38. Найти координаты точки M 2 , симметричной точке

M 0 (1, 2, −1) относительно плоскости P : 3x − y + 2z − 27 = 0 .

Решение. Воспользуемся результатом решения за-

дачи 37. Точка M1 (7, 0, 3) − проекция

точки M 0 на

плоскость. Координаты точки M 2 (x2 , y2 , z2 ) можно най-

ти, используя соотношения:

x0 + x2

= x ,

y0 + y2

= y ,

z0 + z2

= z .

Следовательно,

= 2x1 − x0 = 13,

y2 = 2 y1 − y0 = −2,

z2 = 2z1 − z0 = 7.

Ответ: M 2 (13,

− 2,

7).

Задача 39. Найти координаты проекции M 1 точки M 0

(0, 2, 1) на пря-

мую L :

x − 4

y + 1

z − 2

− 1

Решение. Найдем уравнение плоскости P ,

перпендикулярной прямой L и проходящей через

точку M 0 (0, 2, 1) . В качестве нормального вектора

N плоскости

P можно выбрать

направляющий

вектор s прямой L , т.е. положить N = s (2, −1, 3) .

Тогда уравнение плоскости

P : 2x − ( y − 2) + 3(z − 1) = 0, или 2x − y + 3z − 1 = 0.

Параметрические уравнения прямой L имеют вид

x = 4 + 2t,

= -1 - t,

= 2 + 3t.

Далее решаем аналогично задаче 37. Координаты точки M 1 находим с

помощью формулы (3.5). Получаем t1 = −1,

x1 = 2, y1 = 0, z1 = −1.

Ответ: M1

(2,

0, − 1).

Задача 40. Найти координаты точки M 2 , симметричной точке

M 0 (0, 2, − 1) относительно прямой L :

x − 4

y + 1

z − 2

-1

Решение. Воспользуемся результатом за-

дачи 39. Точка M 1 (2,

0, − 1)

проекция

точки M 0 на прямую L .

Координаты точки M 2 (x2 , y2 , z2 ) можно

найти, используя соотношения:

x0 + x2

= x1 ,

y0 + y2

= y1 ,

z0 + z2

= z1 .

Следовательно,

x2 = 2x1 − x0

= 4,

y2 = 2 y1 − y0 = −2,

z2 = 2z1 − z0

= −3.

Ответ: M 2 (4,

− 2,

− 3).

Задача 41. Найти расстояние между параллельными прямыми

x − 2

y − 3

z + 1

и L2

x − 5

z + 25

- 2

Решение. Нужно вычислить длину перпенди-

куляра d , опущенного из точки

M1 (2, 3,

−1) , че-

рез которую проходит прямая L1 , на прямую L2 .

Для этого построим параллелограмм со сторонами

M1M 2 и s . Здесь M 2 (5, 0, − 25) − точка, через ко-

торую проходит прямая L2 ,

а s −

направляющий

− 2) ). Пло-

вектор прямых (так как прямые параллельны, то s1

= s2

= s (3, 2,

щадь S параллелограмма вычисляется с помощью векторного произведения

векторов M1M 2 (3,

− 3,

− 24) и s (3,

− 2) :

UUUUUUR

M1M 2

´ s

-3

-24

= 3 ×

-1

-8

= 3(18i - 22 j + 5k ),

-2

S =\| M1M	R	+ 484	+ 25	= 3 833 .
	2 ´ s \|= 3 324

Расстояние d получим, разделив площадь параллелограмма S на длину его стороны | s | :

833

d =

= 3

49 = 21.

| s |=

9 + 4

+ 4 =

17,

| s |

Ответ: d = 21.

∙ Полезная формула.

Если заданы две параллельные прямые (L1 || L2 ,

s1 = s2 = s )

L :

x − x1

y − y1

z − z1

L :

x − x2

y − y2

z − z2

то расстояние d между ними вычисляется по формуле

| M M

d =

´ s |

(3.10)

1 2

| s |

Задача 42. Найти расстояние между скрещивающимися прямыми:

x = 2t - 4,

x = 4t - 5,

L1 : y = -t + 4, и

L2 : y = -3t + 5,

z = -2t -1

z = -5t + 5.

Решение. Прямая

проходит через точку M1 (−4,

4, −1) и ее направ-

− 2)

. Прямая L2 прохо-

ляющий вектор

s1 (2, − 1,

дит

через точку M 2 (−5, 5, 5)

и ее направляющий

− 5) . Известно, что, если прямые

вектор

s2 (4, − 3,

скрещиваются, то существуют две параллельные

плоскости P1 и P2 такие, что прямая L1 лежит в

плоскости

P1 ,

а прямая

L2 − в плоскости P2 . На-

правляющие векторы s1 и s2 будут направляющи-

ми векторами этих плоскостей.

Построим параллелепипед, сторонами которо-

го являются векторы M1M

. Найдем его объем. Для этого вычислим

2 , s1, s2

смешанное произведение

M1M 2 × s1 ´ s2 :

UUUUUUR

-1

-1 -2

= -9.

M1M 2 × s1 ´ s2 =

-3

-5

Таким образом, объем V = 9.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.09.20191.79 Mб26Philosophy.doc
#
09.02.20152.22 Mб25physics2.doc
#
09.02.2015430.36 Кб209Phys_LAB_5_READY (1).docx
#
09.02.2015210.97 Кб279Phys_LAB_№11.docx
#
09.02.2015567.81 Кб72Plazma_metod_4-7.doc
#
09.02.2015437.27 Кб12Ploskost_i_pryamaya_v_prostranstve.pdf
#
09.02.20151.71 Mб41Pogr IDZ1.doc
#
09.02.20151.69 Mб38Pogr.doc
#
14.04.2019805.89 Кб10politologiya 1-80.doc
#
09.02.201578.85 Кб8POLOZhENIE_Sovet_Starost_LETI_okonch.doc
#
09.02.20151.01 Mб5Polozova_Maria_MarketoIT#2.pdf