Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ploskost_i_pryamaya_v_prostranstve

.pdf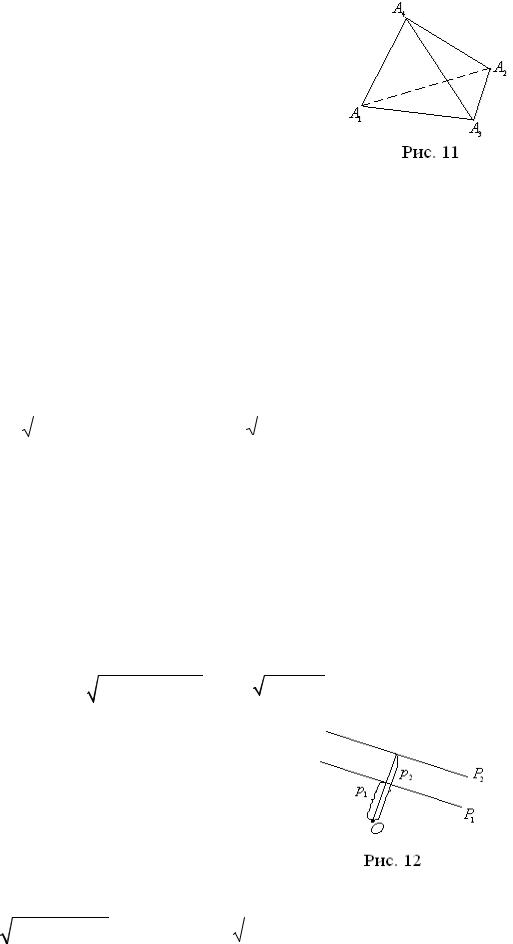

Скачиваний:

Добавлен:

09.02.2015

Размер:

437.27 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

		Решение.		Найдём уравнение грани A1 A2 A3 . Для
этого подставим в формулу (1.11) координаты вер-
шин A1 , A2 , A3 :
	x	y −1	z − 2	= 0 , или 7x + 7(y −1) −14(z − 2) = 0 .
	x	y −1	z − 2
	4	2	3
	5	−1	2

Уравнение искомой грани имеет вид

x + y − 2z + 3 = 0 .

Уравнения граней A1 A2 A4 , A1 A3 A4 ,

A2 A3 A4 найдите самостоятельно.

Ответ: A1 A2 A3 : x + y − 2z + 3 = 0;

A1A2 A4 : x − 5 y + 2z + 1 = 0;

A1A3 A4 : 3x − y − 8z + 17 = 0; A2 A3 A4 : 5x − 3y − 4z − 9 = 0 .

Задача 11. Найти расстояние от точки M 0 (−2, −4, 3) до плоскости

2x − y + 2z + 3 = 0.

Решение. Используем формулу (1.7):

d =

Ax0

+ By0 + Cz0 + D

| 2 × (-2) -1× (-4) + 2 × 3 + 3 |

= 3 .

A2 + B2 + C 2

4 + 1 + 4

Ответ: d = 3.

Задача 12. Найти расстояние между параллельными плоскостями

P1 : x − 2 y − 2z − 6 = 0 и P2 : x − 2 y − 2z − 12 = 0 .

Решение.

Первый способ. Выберем произвольно точку M 0 на плоскости P2 . Пусть,

например, x0 = y0 = 0. Тогда z0

= −6. Следовательно, M 0 (0, 0, −6). Найдем

расстояние d от точки M 0 до плоскости P1 ,

по формуле (1.7):

d =

A1x0 + B1 y0 + C1z0 + D1

12 - 6

= 2.

A12

+ B12 + C12

1 +

4 + 4

Второй способ. Очевидно, что плоскости P1 и

P2 лежат по одну сторону относительно начала ко-

ординат O(0, 0, 0).

Обозначим через p1 расстояние от начала координат до плоскости P1 , через p2 − до плоскости P2 .

p1 =

| D1 |

= 2 ,

p2 =

| D2

= 4.

+ B2

A22 + B22 + C22

+ C 2 3

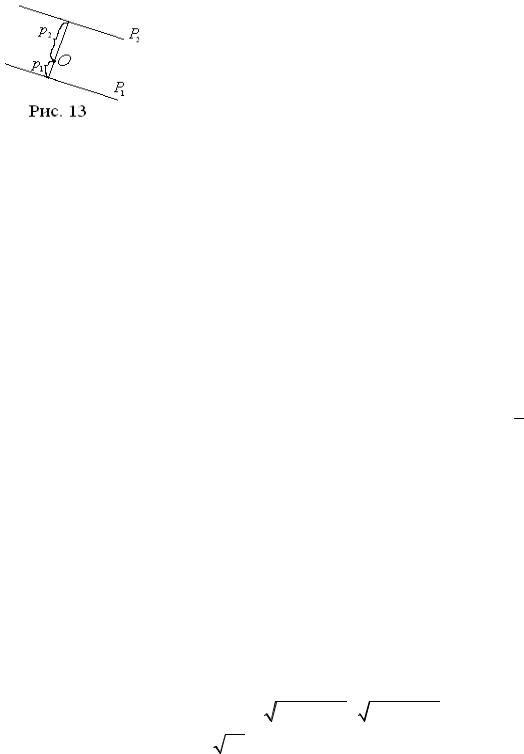
Расстояние между плоскостями равно d = p2 − p1 . Отсюда находим d = 4 − 2 = 2.

Ответ: d = 2.

Замечание. Если бы плоскости находились по разные стороны от начала координат, то расстояние между ними было бы равно d = p1 + p2 .

Задача 13. Составить уравнение плоскости, проходящей через заданную

2x − y + 2z − 3 = 0,		0 (1,	−1, 1), не лежащую на этой
прямую	и точку M
x + 2 y - z -1	= 0

прямой.

Решение. Уравнение произвольной плоскости P , проходящей через заданную прямую, имеет вид (см. формулу (1.8))

α (2x − y + 2z − 3) + β (x + 2 y − z −1) = 0.

Отсюда P : x(2α + β ) + y(−α + 2β ) + z(2α − β ) + (−3α − β ) = 0.

Подставляя в это уравнение координаты точки M 0 , получим

2α + β + α − 2β + 2α − β − 3α − β = 0, или 2α − 3β = 0, α = 3 β . 2

Положим, например, β = 2. Тогда α = 3. Остаётся подставить эти коэффици-

енты в уравнение плоскости. Получим P : 8x + y + 4z −11 = 0.

Ответ: 8x + y + 4z − 11 = 0.

Задача 14. Написать уравнение биссектрисы P острого двугранного уг-

ла между плоскостями 2x − 3y − 4z − 3 = 0 и 4x − 3y − 2z − 3 = 0.

Решение. Нормальные векторы первой и второй плоскостей соответст-

венно равны N1 (2, - 3,

- 4) и N2 (4, - 3, - 2). Они образуют острый уголϕ ,

т.к.

cosϕ =

N1 × N2

2 × 4 - 3 × (-3) - 4 × (-2)

> 0.

| N1

| ×| N2 |

4 + 9 +16 × 16 + 9 + 4

Очевидно, что | N1 |=| N2 |=

(Нормальные векторы N1

и N2

29.

всегда можно

взять равными по длине, например, единичными.) Так как | N1

|=| N2 |, то па-

раллелограмм, построенный на векторах N1 и N2 как на сторонах, является

ромбом, а диагональ N = N1 + N2

биссектрисой его угла. Следовательно,

вектор N (6, − 6, − 6) может быть выбран в качестве нормального вектора

искомой биссектрисы P. Далее следуем рассуждениям задачи 13. Уравнение биссектрисы P ищем в виде

α (2x − 3y − 4z − 3) + β (4x − 3y − 2z − 3) = 0.

Отсюда P : (2α + 4β )x − (3α + 3β ) y − (4α + 2β )z − 3α − 3β = 0.

Учитывая, что 2α + 4β = 6, 3α + 3β = −6, 4α + 2β = 6, получаем систему уравнений

α + 2β = 3,

	α + β = 2,	откуда находим α = 1, β = 1.

2α + β = 3,

Подставляя эти значения в уравнение биссектрисы P , имеем

6x − 6 y − 6z − 6 = 0, или x − y − z − 1 = 0.

Чертеж к этой задаче предлагаем сделать самостоятельно.

Ответ: x − y − z − 1 = 0.

2. ПРЯМАЯ В ПРОСТРАНСТВЕ

2.1.Основные сведения из теории

Прямая L в пространстве может быть задана уравнением одного из следующих видов.

1) Общие уравнения прямой:

A1x + B1 y + C1z + D1	= 0,
L :	(2.1)
A2 x + B2 y + C2 z + D2	= 0,

где коэффициенты A1 , B1 ,C1 не пропорциональны коэффициентам A2 , B2 ,C2 .

Это равносильно заданию прямой как линии пересечения двух плоскостей. 2) Параметрические уравнения прямой:

x = x0 + lt,
y = y0 + mt,	(2.2)
z = z0 + nt.

Здесь (x0 , y0 , z0 ) − координаты какой-либо точки M 0 , принадлежащей пря-

мой L , (l, m, n) − координаты вектора s , параллельного прямой. Вектор s

называется направляющим вектором прямой. Переменная t параметр, − ∞ < t < ∞.

3) Канонические уравнения прямой:

x − x0	=	y − y0	=	z − z0	.	(2.3)
l		m
				n

4)Уравнения прямой, проходящей через две заданные точки M1 (x1, y1, z1 )

иM 2 (x2 , y2 , z2 ) :

x − x1

y − y1

z − z1

(2.4)

x2 − x1

y2 − y1

z2 − z1

Кроме того, нам понадобятся следующие формулы, доказательство ко-

торых можно найти в теоретическом курсе.

5) Угол ϕ между двумя прямыми

L :

x − x1

y − y1

z − z1

x − x2

y − y2

z − z2

равен углу между направляющими векторами s1 (l1 , m1, n1 )

и s2 (l2 , m2 , n2 ) :

l l

+ m m + n n

cosϕ =

× s

cosϕ =

(2.5)

;

1 2

+ m2

+ n2

× l 2

+ m2

l 2

+ n2

Прямые L1 и L2 параллельны тогда и только тогда, когда векторы

R R

коллинеарны ( s1 || s2 ):

l1 = m1 = n1 . l2 m2 n2

Прямые L1 и L2 перпендикулярны тогда и только тогда, когда векторы

R	R	R
s2	ортогональны ( s1	s2 ):

l1l2 + m1m2 + n1n2 = 0.

R R

s1 и s2

(2.6)

s1 и

(2.7)

2.2. Решение типовых задач

Задача 15. Найти канонические уравнения прямой, заданной как линия

пересечения двух плоскостей: x + y + z - 2 = 0,

x - y - 3z + 6 = 0.

Решение. Найдем какую-нибудь точку M 0 на прямой. Положим, напри-

мер, z0 = 0 . Другие координаты получим из системы

x + y = 2,	Очевидно, что x0 = −2, y0					= 4 .
уравнений	Очевидно, что x0 = −2, y0					= 4 .
x − y = −6.
Следовательно, M 0 (−2,	4, 0) . Затем находим направ-
ляющий вектор s прямой. Так как прямая принадле-
жит одновременно обеим плоскостям, то вектор s						ор-
тогонален нормальным векторам этих плоскостей, т.е.
s N1 (1, 1, 1), s N2 (1,	−1, − 3) . Поэтому за направ-
ляющий вектор s можно принять
		R	R	R
		R	R	R
R	R	i	j	k	R	R	R
R	R				R	R	R
s = N1 × N2 =		1 1 1			= −2i + 4 j		− 2k .
		1	−1	−3

Подставляя координаты направляющего вектора s и точки M 0 в уравнения прямой (2.3), получим

x + 2

y − 4

или

x + 2

y − 4

− 2

− 2 1

Ответ:

x + 2

y − 4

− 2

∙ Полезная формула. Если прямая задана как линия пересечения двух

плоскостей:

A1x + B1 y + C1z + D1 = 0,

A x + B y + C

z + D = 0,

то ее направляющий вектор s можно выбрать в виде

	R	R	R
	R	R	R
	i	j	k
s =	A1	B1	C1	.	(2.8)
	A2	B2	C2
Задача 16. Найти параметрические и канонические уравнения прямой,
проходящей через точку M 0 (−4,	2,	2) и параллельной вектору s (3, 1,			−1) .
Решение. Известны точка M 0		и направляющий вектор s прямой.

Согласно формуле (2.2) параметрические уравнения прямой имеют вид

x = −4 + 3t,
	+ t,
y = 2
	− t.
z = 2

Канонические уравнения получаем, используя формулу (2.3):

x + 4

y − 2

z − 2

− 1

x = −4 + 3t,

+ 4

− 2

z − 2

Ответ:

y = 2 + t,

− 1

z = 2 − t.

Задача 17. Найти направляющий вектор

прямой L : x = 2,

y = 4.

Решение. Прямая L проходит через точку

M 0 (2,

4) на плоскости xOy и параллельна оси

Oz . Очевидно, что ее направляющий вектор

можно выбрать в виде

s (0, 0, 1).

Ответ: s (0, 0, 1).

Задача 18. Найти косинусы углов, которые образует прямая

L :

x + 3

2 y − 5

z −1

−4

с осями координат.

Решение. Обозначим через cosα , cos β ,

cosγ

косинусы углов прямой L

с осями Ox ,

Oy и Oz соответственно. Они, очевидно, равны направляющим

косинусам вектора s

прямой. Из уравнений прямой находим

s (3,

− 2,

2) .

Следовательно,

−2

cosα =

; cos β =

;

cosγ =

9 + 4 +

+ 4 +

+ 4 + 4

(Напомним, что cos2 α + cos2 β + cos2 γ = 1.)

Ответ: cosα =

; cos β =

−2

; cosγ =

Задача 19. Найти косинус острого угла между прямыми

L :

x − 4

2 y + 1

z + 3

L :

4x + 1

y − 2

z + 5

−3

−2

Решение. Из уравнений прямых вытекает, что направляющий вектор

прямой

L1 равен

−

− 2 ,

направляющий вектор прямой L2 равен

4) . Для удобства вычислений направляющий вектор прямой L1 вы-

s2 (4, 3,

- 3,

- 4) .

Он коллинеарен исходному. Используя формулу

берем в виде s1 (4,

4 × 4 + (-3) ×3 + (-4) × 4

(2.5), получаем cosϕ =

16 + 9 +16 × 16 + 9 +16 41

Ответ: cosϕ = 9 . 41

	x = 2t,
Задача 20. Показать, что прямая y = 3t, перпендикулярна прямой
		z = t

y + z − 8 = 0,
	= 0.
x − z + 4

Решение. Направляющий вектор первой прямой, очевидно, равен

R	(2, 3, 1)								R	найдем с помощью фор-
s1	(2, 3, 1)	, направляющий вектор второй прямой s2								найдем с помощью фор-
мулы (2.8):
				R	R	R
				R	R	R
				i	j	k	R	R	R
		R					R	R	R
		s2	=	0 1 1			= -i	+ j	- k .
				1	0	-1

Проверим условие ортогональности двух прямых (2.7):

l1l2 + m1m2 + n1n2 = 2 × (-1) + 3 ×1 + 1 × (-1) = 0.

Ответ: прямые перпендикулярны.

Задача 21. Проверить, лежат ли три данные точки M1 (-3, 5, 4) ,

M 2 (2, 4, 6) и M 3 (8, 3, 4) на одной прямой.

Решение. Напишем уравнения прямой, проходящей через две заданные точки M1 (-3, 5, 4) и M 2 (2, 4, 6) , согласно формуле (2.4). Получим

x + 3

y − 5

z − 4

, или

x + 3

y − 5

z − 4

2 + 3 4 - 5 6 - 4

-1

Проверим, удовлетворяют ли координаты точки M 3 (8,

3, 4) этим уравнени-

ям. После подстановки x

= 8, y = 3 получаем:

8 + 3

3 − 5

-1

Следовательно, точка M 3

не лежит на прямой.

Ответ: не лежат.

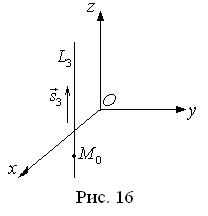
Задача 22. Найти канонические уравнения прямых L1,

L2 , L3 , проходя-

щих через точку M 0 (2, 0,

− 3) параллельно 1) оси Ox ;

2) оси Oy ;

3) оси Oz .

Решение. Найдем уравнения прямой L3 , проходящей через точку M 0 па-

раллельно оси Oz . Её направляющий вектор s3

можно выбрать в виде s3

(0, 0, 1) .

Используя

формулу (2.3), получим L :

x − 2

z + 3

Таким же образом находим L1 и L2 .

L :

x − 2 = y = z + 3 ,

s (1, 0, 0) ;

L2 :

x − 2

z + 3

(0, 1,

0) .

x − 2

z + 3

Ответ: L

;

x − 2

z + 3

;

x − 2

z + 3

x − 3

y + 2

z − 5

Задача 23. Найти точки пересечения прямой L :

−1

плоскостями координат.

Решение. Для того чтобы найти точку пересечения прямой L с плоско-

стью xOy , в канонических уравнениях прямой

L следует положить z = 0 .

Получим

x − 3

y + 2

= −1, откуда x = 4 , y = −4 . Таким образом, прямая L

−1

− 4, 0) . Аналогично находим точки

пересекает плоскость

xOy

в точке (4,

пересечения с плоскостями xOz и yOz .

Ответ: (4, − 4, 0) ; (2, 0, 10) ; (0,

4, 20) .

Задача 24. Известны координаты вершин тетраэдра:

A1 (0, 1, 2);

A2 (4, 3, 5); A3 (5, 0, 4);

A4 (3, 2, 3) . Составить канонические уравнения его ре-

бер и найти их длины.

Решение. Условие задачи такое же, как и в задаче

10. Найдем уравнения ребра A1 A2 . Для этого подставим координаты вершин A1 и A2 в формулу (2.4). Получим

x = y −1 = z − 2 . Теперь можно определить длину реб- 4 2 3

ра A1 A2 :

A1 A2 = ( x2 − x1 )2 + ( y2 − y1 )2 + ( z2 − z1 )2 = 16 + 4 + 9 = 29 .

Уравнения и длины отдельных ребер найдите самостоятельно.

Ответ: 1) A A :						x			=			y −1									=					z − 2										,					A A =												;
						x						y −1														z − 2																				29
																																														29
1	2	4									2																	3													1	2
		4									2																	3
2) A A		:			x				=			y −1								=					z − 2										,						A A =											;
					x							y −1													z − 2																				30
																																													30
1	3	5											−1															2													1	3
		5											−1															2
3) A A :			x						=		y −1								=					z − 2										,							A A =										;
			x								y −1													z − 2																							11
																																															11
1	4	3									1																	1													1	4
		3									1																	1
4) A A		:						x − 4							=			y − 3											=				z − 5						, A A =															;
								x − 4										y − 3															z − 5															11
																																																11
2	3								1												−3															−1					2	3
									1												−3															−1
5) A A :				x − 4									=			y − 3											=					z − 5						,			A A =									;
				x − 4												y − 3																z − 5																	6
																																																	6
2	4								1							1												2													2	4
									1							1												2
6) A A		:					x − 5							=			y						=							z − 4							,				A A = 3 .
6) A A		:												=									=														,				A A = 3 .
3	4								2									−2										1													3	4
									2									−2										1
Задача 25. Найти точку пересечения двух прямых
L :	x + 2									=				y		=						z −1									и L :										x − 3		=	y −1											=	z − 7	.
L :										=		−3				=															и L :												=												=	2	.
1		2										−3				4																								2	3	4														2
1																																								2

Решение. Перепишем уравнения прямых в параметрическом виде

	x = −2 + 2t1,				x = 3 + 3t2 ,
L1		,		L2		+ 4t2 ,
L1	: y = −3t1	,	и	L2	: y = 1	+ 4t2 ,
	z = 1 + 4t				z = 7 + 2t		.
		1				2

Для нахождения точки пересечения этих прямых нужно решить систему уравнений:

	−2 + 2t = 3 + 3t ,					3t			− 2t		= −5,
			1	2				2		1	= −1,
−3t1		= 1 + 4t2 ,			или 4t2 + 3t1						= −1,
1 + 4t			= 7 + 2t	,	t		2	− 2t		= −3.
		1	2				2		1

Очевидно, она имеет единственное решение t1 = 1, t2 = −1. Подставляя значе-

ние параметра t1 в параметрические уравнения прямой L1 (или t2 в уравнения прямой L2 ), получим x0 = −2 + 2 = 0, y0 = −3, z0 = 1 + 4 = 5.

Ответ: M 0 (0, − 3, 5) .

Задача 26. Найти биссектрису L острого угла между прямыми

L :

x + 2

z −1

и L

x − 3

y −1

z − 7

-3

Решение. Точку пересечения этих прямых M 0

(0, − 3, 5) мы нашли, ре-

шая задачу 25. Убедимся теперь, что направляющие векторы

s1 (2, − 3, 4) и

s2 (3, 4, 2) прямых L1 и L2 образуют острый угол. Действительно,

2 ×3 + (-3)

× 4 + 4 × 2

cosϕ =

> 0.

4 + 9 +16 × 4 + 9 +16 29

29 . (Направляющие векторы s1

и s2

Очевидно, что

всегда можно

взять равными по длине, например, единичными.) Так как

, то парал-

лелограмм, построенный на векторах

как на сторонах,

является ром-

s1 и

бом, а диагональ

− биссектрисой его угла. Следовательно, вектор

s = s1

+ s2

s (5, 1, 6) может быть выбран в качестве направляющего вектора биссектри-

сы L .

Таким образом, известно, что искомая прямая проходит через точку

M 0 (0, − 3, 5),

и ее направляющий вектор равен s (5, 1, 6) . Запишем канони-

ческие уравнения L согласно формуле (2.3):

y + 3

z − 5

Чертеж к этой задаче предлагаем сделать самостоятельно.

Ответ:

y + 3

z − 5

3. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ

3.1. Основные сведения из теории

Пусть прямая задана каноническими уравнениями

L : x − x0 = y − y0 = z − z0 , l m n

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.09.20191.79 Mб26Philosophy.doc
#
09.02.20152.22 Mб25physics2.doc
#
09.02.2015430.36 Кб209Phys_LAB_5_READY (1).docx
#
09.02.2015210.97 Кб279Phys_LAB_№11.docx
#
09.02.2015567.81 Кб72Plazma_metod_4-7.doc
#
09.02.2015437.27 Кб12Ploskost_i_pryamaya_v_prostranstve.pdf
#
09.02.20151.71 Mб41Pogr IDZ1.doc
#
09.02.20151.69 Mб38Pogr.doc
#
14.04.2019805.89 Кб10politologiya 1-80.doc
#
09.02.201578.85 Кб8POLOZhENIE_Sovet_Starost_LETI_okonch.doc
#
09.02.20151.01 Mб5Polozova_Maria_MarketoIT#2.pdf