Метод Дэвидона
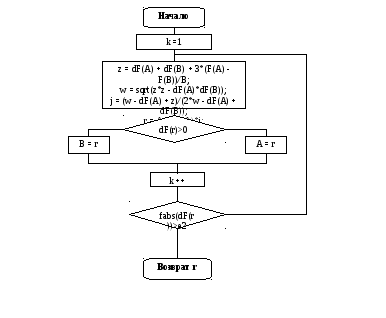
Текст программы:
#include <windows.h>
#include <conio.h>
#include <iostream>
#include <math.h>
using namespace std;
/***************************Структуры*****************************/
struct Dot {
double x1,x2; };
struct grad {
double g1,g2; };
struct Vek {
double x1,x2,len; };
/*************************Глобалочки******************************/
Dot x; Vek p; double a,b;
/******************************Функция*********************************/
double f(double t) {
Dot x2 ;
x2.x1=x.x1+t*p.x1;
x2.x2=x.x2+t*p.x2;
return x2.x1*x2.x1+3*x2.x2*x2.x2+2*x2.x1*x2.x2;}
/**************************производная******************************/
double df(double t) {
Dot x2;
x2.x1=x.x1+t*p.x1;
x2.x2=x.x2+t*p.x2;
return ((-400*(x2.x2-x2.x1*x2.x1)*x2.x1-2*(1-x2.x1))*p.x1+200*(x2.x2-x2.x1*x2.x1)*p.x2);
}
/**********************Antigradientnoe napravlenie***************************/
void napr()
{
p.x1=400*(x.x2-x.x1*x.x1)*x.x1+2*(1-x.x1);
p.x2=-200*(x.x2-x.x1*x.x1);
}
/****************************Metod Svenna 4**********************************/
void Swann4(double t)
{
double s=0;
if(t>fabs((f(0)-df(0))/df(0)))
t=fabs((f(0)-df(0))/df(0));
if(df(0)>0)
{ p.x1=-p.x1;
p.x2=-p.x2;
}
do
{
s=s+t;
t=2*t;
}
while((df(0)*df(s))>0);
a=s-t/2;
b=s;
}
/***************************Ras4etnie formuli********************************/
double gam(double c)
{
double z,w;
z=df(a)+df(b)+3*(f(a)-f(b))/b;
w=sqrt(z*z-df(a)*df(b));
c=a+((z-df(a)+w)/(df(b)-df(a)+2*w))*(b-a);
return c;
}
/*****************************Metod Devidona*********************************/
double Davidon(double e)
{
double c=0;
Swann4(1);
do
{
c=gam(c);
if(df(c)<0)
a=c;
else
b=c;
}
while(fabs(df(c))>e);
return c;
}
/******************************Metod Koshi***********************************/
void KOSHI(double e)
{
double alfa;
Dot x2;
int g=0;
x.x1=-1.2;
x.x2=1;
x2.x1=x.x1;
x2.x2=x.x2;
do
{
g++;
x.x1=x2.x1;
x.x2=x2.x2;
napr();
alfa=Davidon(e);
x2.x1=x.x1+alfa*p.x1;
x2.x2=x.x2+alfa*p.x2;
}
while((sqrt(pow((x2.x1-x.x1),2)+pow((x2.x2-x.x2),2))>e)||(fabs(f(0)-f(alfa))>e));
x.x1=x2.x1;
x.x2=x2.x2;
cout<<"\nKolli4estvo iteraciy: k = "<<g;
}
/***************************Osnovnaya programma******************************/
void main()
{
x.x1=-2;
x.x2=-2 ;
double e;
cout<<"\n\n\nCelevaya funkciya: 100(x2-x1^2)^2+(1-x1)^2";
cout<<"\nNa4al'naya to4ka poiska: Xo = ( -1.2 ; 1 )";
cout<<"\nVvedite to4nost' poiska: E = ";
cin>>e;
KOSHI(e);
cout<<"\nRezul'tat minimizacii: ";
cout<<"( "<<x.x1<<" ; "<<x.x2<<" )";
cout<<endl;
}
Результаты тестирования метода:
Ниже приведена таблица с результатами работы программы для функции f(x) = 100(x2 - x12)2 + (1 - x1)2, с различными стартовыми точками и точностями вычисления.
|
Точность: |
|
0.0001 |
|
0.00001 |
|
0.000001 |
|
Метод Коши |
К |
x* |
K |
x* |
K |
x* |
|
X0=(1.2,1) |
6241 |
(0.999902, 0.999803) |
9625 |
(0.999991, 0.999981) |
14207 |
(0.999999, 0.999998) |
|
X0=(1.5,2) |
614 |
(1.00011, 1.000221) |
812 |
(1.000011, 1.000022) |
1106 |
(1.000001, 1.000002) |
|
X0=(-2,-2) |
5704 |
(0.999899, 0.999797) |
7410 |
(0.99999, 0.99998) |
9114 |
(0.999999, 0.999998) |
Графическая интерпретация:
Выводы:
В данной работе был использован метод Свенна4 и метод Дэвидона для получения оптимального шага. Поиск ведется в пространстве, начиная с заданной начальной точки x0 по антиградиентному направлению p0. И в результате выполнения метода Коши находится оптимальный шаг, доставляющий минимум в результате исчерпывающего спуска вдоль антиградиентного направления pк. Полученный шаг соответствует точке x* = xк+1 . Большое количество итераций и неточность минимума объясняется тем, что вблизи минимума для реальных (овражных) функций метод зацикливается, либо рыскает и останавливается.
Ответы на контрольные вопросы: