Вычисление определенного интеграла по частям.
Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур. Примеры.
Основными геометрическими приложениями определенного интеграла являются: вычисление площади плоской фигуры, вычисление объемов тел вращения вокруг осей координат и вычисление длины дуги плоской кривой.
Телом
вращения вокруг
оси Ох называется
фигура, полученная от вращения вокруг
оси 
криволинейной
трапеции, ограниченной графиком
непрерывной на отрезке 
кривой 
и
прямыми 
, 
и
(Рис.17).
Объем тела вращения вокруг оси определяется по формуле:
.
Если
функция
и
ее производная
непрерывны
на отрезке
,
то длина дуги кривой на отрезке
определяется
по формуле:
Вычисление площадей плоских фигур в декартовых координатах
Площадь
плоской фигуры, ограниченной непрерывной
на отрезке 
кривой 
,
осью
,
а также вертикальными прямыми
и
(площадь
криволинейной трапеции – рис. 12),
определяется по формуле:
.
Если график функции расположен ниже оси (Рис. 13), то площадь фигуры определяется по формуле:
.
Площадь
фигуры, ограниченной кривыми 
и 
,
прямыми
и
,
при условии, что 
(Рис.
14), определяется по формуле:
.
Замечание:
Если плоская фигура имеет сложную форму,
то прямыми, параллельными оси 
,
ее следует разбить на части таким
образом, чтобы можно было применять уже
известные формулы.
Пример
Вычислить площадь фигур, ограниченных линиями:
а) 
;
б)
.
Решение.
а)
Фигура
ограничена осью
(
)
и параболой 
на
отрезке 
.
Построим параболу. Найдем точки пересечения параболы с осью . Для этого приравняем :
; 
;
;
.
Найдем координаты вершины параболы:
,
.
Парабола
имеет
вершину в точке с координатами 
и
ветви ее направлены вверх.
Фигура, ограниченная заданными линиями изображена на рис. 15.
Площадь искомой фигуры равна сумме площадей двух криволинейных трапеций:
.
Найдем искомую площадь:
(ед2)
(ед2)
Тогда площадь заданной плоской фигуры равна:
(ед.2).
б)
Фигура
ограничена параболой 
и
прямой 
.
Построим данные параболу и прямую (рис. 16).
Найдем границы интегрирования, т.е. точки пересечения прямой и параболы. Для этого решим систему, составленную из уравнений этих линий:
; 
;
;
;
;
.
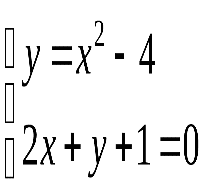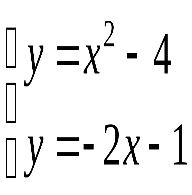Следовательно,
парабола и прямая пересекаются в точках
с абсциссами 
и
.
Площадь фигуры определяем по формуле:
,
где
линией
является
прямая
(ограничивает
фигуру сверху), алинией
является
парабола
(ограничивает
фигуру снизу).
(ед.2).
Несобственные интегралы с бесконечными пределами интегрирования. Примеры.
В предыдущих лекциях мы рассматривали интегралы от функций, интегрируемых на конечных отрезках интегрирования. На практике возникает необходимость обобщения этих понятий на случаи, когда либо один из концов (или оба) отрезка интегрирования удален в бесконечность, либо функция не ограничена на отрезке интегрирования.
Пусть
функция 
определена
на промежутке 
и
интегрируема по любому отрезку
т.е.
существует определенный интеграл
при
любом 
Тогда,
если существует конечный предел
то его называют несобственным интегралом первого рода и обозначают
Таким образом, по определению,
Если данный предел не существует или бесконечен, то несобственный интеграл не существует или расходится.
Аналогично
вводится несобственный интеграл по
промежутку 
Несобственный интеграл с двумя бесконечными пределами можно определить как сумму выше рассмотренных несобственных интегралов
где -любое число, при условии существования обоих интегралов справа.
Геометрический смысл несобственного интеграла первого рода.
Пусть 
тогда
определенный интеграл
выражает
площадь области, ограниченной сверху
графиком функции 
снизу
– осью
слева
– прямой
справа
– прямой 
Несобственный интеграл
выражает
конечную площадь бесконечной области,
ограниченной сверху графиком функции 
,
снизу осью
,
слева прямой
Рассмотрим пример вычисления несобственного интеграла первого рода.
т.е. данный интеграл сходится.
Рассмотрим пример.
интеграл расходится, так как
В рассмотренных примерах вычисление несобственного интеграла было основано на его определении.