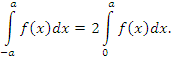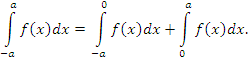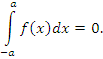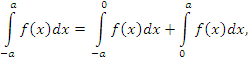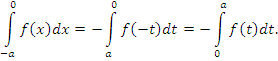- •Дифференциал функции и его свойства.
- •Первообразная функция и неопределенный интеграл.
- •Неопределенный интеграл Определение:
- •Свойства неопределенного интеграла. Свойства неопределённого интеграла
- •Интегралы от основных элементарных функции (таблица интегралов).
- •Метод разложения интегрирования неопределенных интегралов. Примеры.
- •Таким образом, алгоритм действий следующий:
- •Интеграл примет вид
- •Интегрирование тригонометрических функций. Примеры.
- •Интегрирование биномиальных дифференциалов. Примеры.
- •Определенный интеграл и его геометрический смысл. Примеры.
- •Достаточные условия существования определенного интеграла.
- •Свойства определенного интеграла.
- •Теорема о среднем.
- •Определенный интеграл как функция верхнего предела.
- •Свойства определенного интеграла как функции верхнего предела.
- •Формула Ньютона-Лейбница для вычисления определенного интеграла. Формула Ньютона–Лейбница
- •Замена переменной в определенном интеграле. Примеры.
- •Определенный интеграл от четной и нечетной функции на симметричном интервале.
- •Вычисление определенного интеграла по частям.
- •Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур. Примеры.
- •Вычисление площадей плоских фигур в декартовых координатах
- •Несобственные интегралы с бесконечными пределами интегрирования. Примеры.
- •Несобственные интегралы от неограниченных функций. Примеры.
Замена переменной в определенном интеграле. Примеры.
Во многих случаях подынтегральное выражение не позволяет сразу же найти интеграл по таблице. Тогда введение новой переменной интегрирования помогает свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной.
Вводится новая переменная, назовём её t. Например,
в интеграле
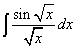 можем
ввести новую переменную
можем
ввести новую переменную  ;
;в интеграле
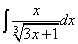 можем
ввести новую переменную
можем
ввести новую переменную 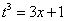 ;
;в интеграле
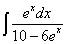 можем
ввести новую переменную
можем
ввести новую переменную 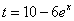 .
.
Далее dx определеяем как дифференциал по переменной t. После этого интеграл можно найти по таблице интегралов. Заменив обратно t на функцию от x, находим данный интеграл окончательно.
Прежде чем перейти к подробным решениям примеров, следует привести теорему, в которой обобщаются перечисленные выше действия.
Теорема. Пусть
функция ![]() определена
и дифференцируема на некотором
промежутке Т и
пусть Х –
множество значений этой функции, на
котором определена функция f(x).
Тогда, если на множестве Х функция f(x)
имеет первообразную, то на
множестве Т справедлива
формула
определена
и дифференцируема на некотором
промежутке Т и
пусть Х –
множество значений этой функции, на
котором определена функция f(x).
Тогда, если на множестве Х функция f(x)
имеет первообразную, то на
множестве Т справедлива
формула
![]() (1)
(1)
Формула (1) называется формулой замены переменной в неопределённом интеграле.
Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.
Пример 1. Найти неопределённый интеграл методом замены переменной:
![]()
Решение. Производим замену x − 1 = t; тогда x = t + 1. Отсюда dx = dt. По формуле (1)
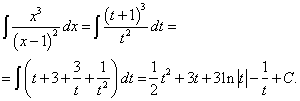
Возвращаясь к переменной x, окончательно получаем
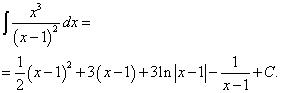
Определенный интеграл от четной и нечетной функции на симметричном интервале.
Теорема 1. Пусть f(x) – интегрируемая на промежутке [-a,a] четная функция:
Тогда интеграл от f(x) в симметричных пределах равен удвоенному интегралу по половинному промежутку:
Для доказательства представим исходный интеграл в виде суммы двух интегралов:
Преобразуем первый интеграл в правой части этого равенства, выполнив подстановку x = – st:
Утверждение доказано. Теореиа 2. Пусть f(x) – интегрируемая на промежутке [-a,a] нечетная функция:
Тогда интеграл от f(x) в симметричных пределах равен нулю:
Теорема доказывается аналогичным образом:
|