15. Теорема о среднем.

 Теорема 5. Если f(x) - непрерывная функция, заданная на промежутке [a, b], то существует такая точка  , что

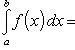
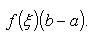     (14)

     В самом деле, пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму

     Так как при всех k будет m ≤ f(ξ_k) ≤ M, а x_k+1 > x_k, то m(x_k+1 - x_k) ≤ M(x_k+1 - x_k). Складывая такие неравенства и замечая, что

получим:

m(b - a) ≤ σ ≤ M(b - a).

     Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b - a к новому неравенству

     Таким образом, частное

есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (14).

     Заметим, что равенство (14) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a > b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b.

     Теорему 5 обычно называют теоремой о среднем значении. Из нее вытекает ряд свойств интеграла, выражающихся неравенствами.

16. Определенный интеграл как функция верхнего предела.

Рассмотрим функцию  . Эту функцию называют: интеграл как функция верхнего предела. Отметим несколько свойств этой функции.

Теорема 2.5. Если   интегрируемая на   функция, то   непрерывна на  .

Доказательство. По свойству 9 определенного интеграла (теорема о среднем) имеем  , откуда, при  , получаем требуемое.

Теорема 2.6. Если   непрерывная на   функция, то функция   дифференцируема на   и  .

Доказательство. По свойству 10 определенного интеграла (вторая теорема о среднем), имеем   где С – некоторая точка отрезка  . В силу непрерывности функции  Получаем

.

Доказанная теорема решает задачу восстановления первообразной для непрерывной функции с помощью интеграла как функции верхнего предела и даёт конструктивное доказательство (то есть доказательство с построением объекта, существование которого утверждается) теоремы 1.1. Более того, если функция   имеет на отрезке   конечное число точек разрыва первого рода, то, разбивая отрезок   на участки непрерывности функции  , получаем, что с помощью интеграла как функции верхнего предела можно восстановить обобщённую первообразную и в этом случае, а заодно и установить справедливость теоремы 1.2.

Таким образом,  - одна из первообразных функции   следовательно,  Где  - другая первообразная   Далее, так как   то   следовательно,   и поэтому 

17. Свойства определенного интеграла как функции верхнего предела.

18. Формула Ньютона-Лейбница для вычисления определенного интеграла. Формула Ньютона–Лейбница

Пусть f (х) данная функция, F её произвольная первообразная.

\int_{a}^{b} f(x) dx =F(x)|_{a}^{b}∫ab​f(x)dx=F(x)∣ab​= F(b) — F(a)

 

где F(x) - первообразная для f(x)

То есть, интеграл функции f (x) на интервале [a;b] равен разности первообразных в точках b и a.