12. Определенный интеграл и его геометрический смысл. Примеры.

13. Достаточные условия существования определенного интеграла.

Своеобразие предельного перехода в определении интеграла может привести к убеждению, что определенный интеграл существует лишь в исключительных случаях. Ниже приведен ряд утверждений, показывающий, что класс интегрируемых функций достаточно богат и охватывает широкий круг функций, используемых в практических задачах.

Теорема 2.5. Если функцияf (x) интегрируема на отрезке[a,b], то она ограничена на этом отрезке.

Теорема 2.6. Если функцияf (x) непрерывна на отрезке[a,b], то она интегрируема на этом отрезке.

Теорема 2.7. Если функцияf (x) определена и монотонна на отрезке[a,b], то она интегрируема этом отрезке.

Теорема 2.8. Если функцияf (x) ограничена на отрезке[a,b]

и непрерывна во всех точках этого отрезка, за исключением конечного числа точек, где функция имеет разрыв первого рода, то эта

функция интегрируема на отрезке [a,b].

Теорема 2.9. Если интегрируемую на[a,b] функцию изменить

в конечном числе точек, то получится интегрируемая функция с тем же интегралом.

В качестве функции, которая не является интегрируемой по Риману можно привести функцию Дирихле на отрезке [0,1]:

1,	если x	рациональное;
f (x) =	если x	иррациональное.
0,

14. Свойства определенного интеграла.

Интегральное исчисление строится на базе набора свойств определенного интеграла. Приведем наиболее важные из них:

1.	∫a	f (x)dx = 0, еслиf (x) определена в точкеa ;
	a
2.	∫a	f (x)dx= −∫b	f (x)dx, еслиf (x) интегрируемая на[a,b].

ba

Очевидным является факт, что значение определенного интеграла для интегрируемой на [a,b]функцииf (x) не зависит от обозначения переменной интегрирования:

∫b	f (x)dx= ∫b	f (t)dt= ∫b	f (z)dz.
a	a	a

56

Теорема 2.10. Если функции			f (x) иg(x) интегрируемы на
отрезке [a,b], то для любых действительных чиселα иβ										функ-
ция α f (x)+ β g(x)	также интегрируема на							[a,b] и справедливо
равенство
∫ab (α f(x) + β g(x))dx= α ∫b					f (x)dx+ β ∫b g(x)dx				(2.6)
Теорема 2.11. Если функция			a				a
			f (x) интегрируема на отрезках
[a,c] и[c,b], то она интегрируема и на отрезке[a,b], причем
∫b	f (x)dx= ∫c	f (t)dx+ ∫b (z)dz,								(2.7)
a	a					c

Теорема 2.12 (теорема о среднем в определенном интеграле) .

Если функция f (x) непрерывна на отрезке[a,b],		то существует
хотя бы одна точка c [a,b], такая, что
∫b	f (x)dx= f(c)(b−a)	(2.8)
a

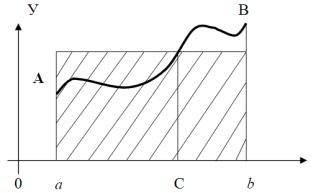
Равенство (2.8) с геометрической точки зрения означает, что площадь криволинейной трапеции aABb совпадает с площадью некоторого прямоугольника (рис.2.2)

Рис. 2.2

57

Теорема 2.13. Еслиf (x)≤ g(x) для всехx [a,b], а		f (x) и
g(x) интегрируемы на[a,b], то
∫b	f (x)dx≤ ∫b g(x)dx	(2.9)