5. Метод разложения интегрирования неопределенных интегралов. Примеры.

Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интегралаприводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Таким образом, алгоритм действий следующий:

1. тождественное преобразование подынтегральной функции;

2. применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов;

3. использование таблицы интегралов.

В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла.

При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования.

6. Метод замены переменной (метод подстановки) интегрирования неопределенных интегралов. Примеры.

7. Метод интегрирования неопределенных интегралов по частям. Примеры.

8. Интегрирование простейших рациональных дробей. Примеры.

9. Интегрирование некоторых видов иррациональностей. Примеры.

1. Интегралы вида  , где    несократимые обыкновенные дроби. Следует сделать подстановку   где s – общий знаменатель дробей  , т. е. наименьшее общее кратное n, …, g. Тогда  , каждая дробная степень выразится через целую степень t и подынтегральная функция преобразуется в рациональную функцию от t, что позволяет избавиться от иррациональности.

2. Интегралы вида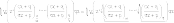

Нужно сделать подстановку  , где s – наименьшее общее кратное знаменателей n, …, g. Тогда   и подынтегральная функция преобразуется в рациональную функцию от t.

П р и м е р  15.  Найти интеграл  .

 

Решение.  ;  ;  .

 

Интеграл примет вид

.

3. Интегралы вида  .

Выделим полный квадрат в выражении  , сделаем подстановку  , обозначим  . Тогда интеграл примет вид

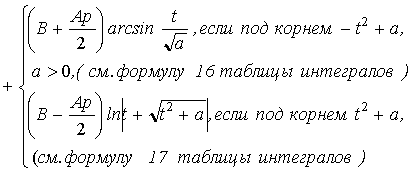В ответе t заменить на  .

П р и м е р  16.  Найти интеграл  .

Решение.  ,  ,  .

Интеграл примет вид

4. Интегралы вида 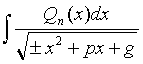 , где Q_n(x)  многочлен степени n(n > 1).

,где Q_n-1(x) – неизвестный многочлен (n1)-й степени, λ – неизвестное число.

Дифференцируя левую и правую части равенства по x, получим

  .

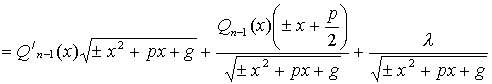Умножая это равенство на  , получим

Методом неопределенных коэффициентов можно найти коэффициенты Q_n-1(x) и λ, и затем останется вычислить только  .

5. Интегралы вида  .

С помощью подстановки   указанные интегралы приводятся к интегралам вида 3 или 4. В самом деле,

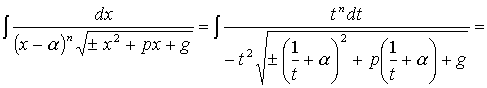
Под корнем после преобразований получается квадратный трехчлен.

10. Интегрирование тригонометрических функций. Примеры.

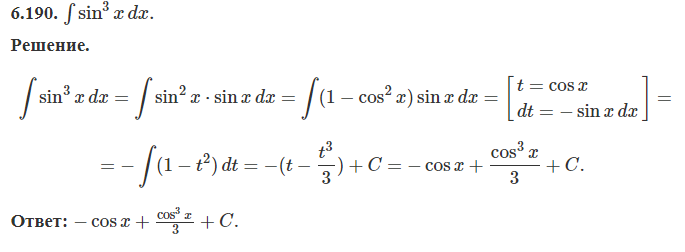
11. Интегрирование биномиальных дифференциалов. Примеры.

Дифференциальным биномом называют выражение вида

где a и b — любые константы, а показатели степеней m, n и p — рациональные числа. Изучим вопрос об интегрируемости в элементарных функциях дифференциальных биномов. Рассмотрим три случая , когда интеграл от дифференциального бинома допускает рационализирующую подстановку. 1. Первый случай соответствует целому p. Дифференциальный бином представляет собой дробно-линейную иррациональность вида  , где r — наименьшее общее кратное знаменателей рациональных чисел m и n. Стало быть, интеграл от дифференциального бинома в этом случае рационализируется подстановкой  . 2.Второму случаю соответствует целое число  . Сделаем подстановку  и положим для краткости  , получим

Подынтегральная функция в правой части является дробно-линейной иррациональностью следующего вида вида  , где s — знаменатель рационального числа p. Таким образом, для второго случая дифференциальный бином рационализируется подстановкой

3. Третьему случаю соответствует целому число  . Подынтегральная функция в правой части является дробно-линиейной иррациональностью вида  , так что интеграл от дифференциального бинома рационализируется подстановкой вида

В середине 19-го века П.Л.Чебышев доказал, что указанными выше тремя случаями исчерпываются все случаи, когда дифференциальный бином интегрируется в элементарных функциях. (Мемуар 1853 года «Об интегрировании иррациональных дифференциалов»).

Примеры

1)Вычислить интеграл  . Здесь  .  Так как p — целое, значит используем подстановку из первого случая

подставим: