
- •§ 18. Понятие, предел и непрерывность функции нескольких переменных
- •§ 19. Частные производные и дифференциал функции нескольких переменных
- •§ 20. Экстремум функции нескольких переменных. Наибольшее и наименьшее значения функции в замкнутой области
- •§ 21. Касательная плоскость и нормаль к поверхности
- •§ 22. Производная по заданному направлению. Градиент
- •§ 23. Неявные функции, их дифференцирование
§ 21. Касательная плоскость и нормаль к поверхности
В
где функции
![]() дифференцируемы на отрезке
дифференцируемы на отрезке![]() .
Возьмем
.
Возьмем![]() и соответствующую ему точкуМ кривой.
Дадимtприращение
и соответствующую ему точкуМ кривой.
Дадимtприращение![]() такое, что
такое, что![]() .
Обозначим соответствующую точку черезN. Проведем секущуюMN. Ее уравнение (см.
аналитическую геометрию)
.
Обозначим соответствующую точку черезN. Проведем секущуюMN. Ее уравнение (см.
аналитическую геометрию)![]() ,
,![]() .
Пусть кривая задана параметрически
уравнениями
.
Пусть кривая задана параметрически
уравнениями![]() ,
,
z
N
М
О у
х





где Х,Y,Z
– текущие координаты прямой (секущей).
Разделим все знаменатели на![]() :
:
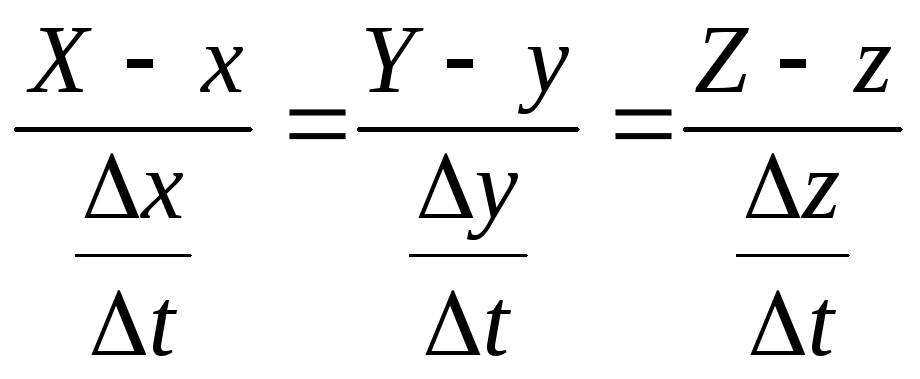 .
.
Ясно, что секущая займет положение
касательной, когда точка N
совпадет с точкойМ при стремленииN кМпо
кривой. Следовательно уравнение
касательной получится тогда, когда
перейдем к пределу при![]() ,
получим
,
получим
![]() – (21.1)
– (21.1)
искомое уравнение касательной.
Замечание.В случае плоской кривой![]() и уравнение касательной прямой, очевидно,
имеет вид
и уравнение касательной прямой, очевидно,
имеет вид![]() .
.
Теперь получим уравнение касательной
плоскости к поверхности
![]() в
в
т
z N
T
M
S
x
y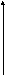







![]() .
Пусть функция
.
Пусть функция![]() дифференцируема в точкеМ. Проведем
через
дифференцируема в точкеМ. Проведем
через
точку М линиюMS,
принадлежащую поверхности![]() .
Пусть ее уравнение в параметрической
форме будет
.
Пусть ее уравнение в параметрической
форме будет![]() .
Если функциих(t),у(t),z(t)
дифференцируемы в точкеt,
которой соответствует точкаМ, то
уравнение касательнойMT
к кривойMS имеет
вид (21.1). Поскольку криваяMS
принадлежит поверхности, имеем
.
Если функциих(t),у(t),z(t)
дифференцируемы в точкеt,
которой соответствует точкаМ, то
уравнение касательнойMT
к кривойMS имеет
вид (21.1). Поскольку криваяMS
принадлежит поверхности, имеем![]() .
Отсюда
.
Отсюда![]()
![]()
![]() (21.2)
(21.2)
в точке М. Введем в рассмотрение прямуюMN:
 ,
(21.3)
,
(21.3)
где
![]() вычислены в точкеМ. Из (21.1), (21.2) и
(21.3) видим, что прямыеMT
иMN перпендикулярны.
Поскольку прямаяMN
не зависит от выбора кривойMS
(зависит только от уравнения поверхности
и от точкиМ), прямаяMN
перпендикулярна касательной к любой
кривой на поверхности, проходящей через
точкуМ. Поэтому все эти касательные
лежат в одной плоскости. Эта плоскость
и называетсякасательной плоскостью
к данной поверхности в точкеМ.
Из аналитической геометрии известно,
что уравнение плоскости, проходящей
через точку
вычислены в точкеМ. Из (21.1), (21.2) и
(21.3) видим, что прямыеMT
иMN перпендикулярны.
Поскольку прямаяMN
не зависит от выбора кривойMS
(зависит только от уравнения поверхности
и от точкиМ), прямаяMN
перпендикулярна касательной к любой
кривой на поверхности, проходящей через
точкуМ. Поэтому все эти касательные
лежат в одной плоскости. Эта плоскость
и называетсякасательной плоскостью
к данной поверхности в точкеМ.
Из аналитической геометрии известно,
что уравнение плоскости, проходящей
через точку![]() и перпендикулярной прямой (21.3), имеет
вид
и перпендикулярной прямой (21.3), имеет
вид
![]() .
(21.4)
.
(21.4)
Прямая MN, перпендикулярная к касательной плоскости и проходящая через точку касания, называетсянормалью к поверхности в точкеМ. Уравнение нормали имеет вид (21.3).
Если поверхность задана уравнением
![]() ,
то представляем его в виде
,
то представляем его в виде![]() .
Тогда
.
Тогда![]() и уравнение касательной плоскости
примет вид
и уравнение касательной плоскости
примет вид
![]() .
.
Пример. Найдем уравнения касательной
плоскости и нормали к поверхности![]() в точке
в точке![]() .
.
Решение. Имеем![]() ,
поэтому уравнение касательной плоскости
(21.4) имеет вид
,
поэтому уравнение касательной плоскости
(21.4) имеет вид
![]() или
или![]() ,
т.е.
,
т.е.![]() (здесь
(здесь![]() –
координаты текущей точки касательной
плоскости).
–
координаты текущей точки касательной
плоскости).
Уравнение нормали:
![]() .
.
