§ 19. Частные производные и дифференциал функции нескольких переменных

Рассмотрим функцию двух переменных , определенную в некоторой области. Возьмем в областипроизвольную точку, придадим аргументух приращение, а аргументу оставим без изменения, т.е. перейдем от точкик точке, тоже принадлежащей области.Тогда функция получитчастное приращение , соответствующее приращениютолько одного аргументах: =. Составим отношение. Если существует конечный предел этого отношения при, то он называетсячастной производной функциипо независимой переменнойхв точкеи обозначаетсяили. Иными словами,

===.

Аналогично определяются частная производная функции по независимой переменнойув точке:

===

и частные производные функции любого числа переменных. Например, для функции

===.

Из определения частной производной следует и правило для нахождения частных производных. Например, чтобы найти частную производную функции пох в точке, нужно считать аргументу постоянным и дифференцироватькак функцию одной переменнойх. Затем в полученное выражение вместох иу подставитьи.

Пример 1. Найдем частные производныеифункциив точке.

Решение. Имеем

=,;=,.

Подсчитаем теперь изменение функции при переходе от точкик точкеобласти определения функции. Разность значений функции в точкахиМ называетсяполным приращением функциипри переходе из точкиМ в точку, обозначаетсяили, т.е.==–. При переходе из точкиМ в точкуаргументы тоже получают приращенияи. Тогдаможно записать в виде. Геометрически полное приращение функции означает приращение аппликатыz при переходе из точкиМ в точку.

При определении дифференциала функции одной переменной важную роль играла форма записи приращения функции . Если, гдепри, то функциюназывали дифференцируемой, а первое слагаемое в выражении для– дифференциалом функции. Аналогичная ситуация имеет место и в случае функции нескольких переменных.

Определение 1. Функцияназываетсядифференцируемой в точке, если ее полное приращение в этой точке можно представить в виде

, (19.1)

где А иВ не зависят от приращенийи, аи– некоторые функции оти, стремящиеся к нулю прии. Выражениеназываетсяполным дифференциаломфункциии обозначаетсяили, а его слагаемыеиназываютсячастными дифференциалами функциипохи поу соответственно и обозначаютсяи.

Таким образом, =,=,=, гдеА иВ не зависят оти.

Теорема 1. Если функциядифференцируема в точке, то она непрерывна в этой точке.

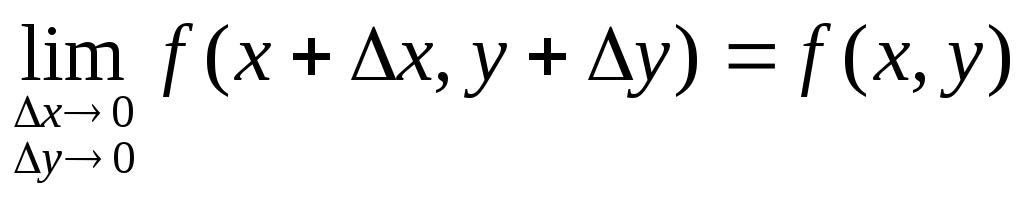Доказательство. В силу дифференцируемости функции в точкеможно записать. Отсюда следует, чтоприи, т.е.. Следовательно,или, что и означает непрерывность функциив точке. Теорема доказана.

Теорема 2 (необходимое условие дифференцируемости функции). Если функциядифференцируема в точке, то она в этой точке имеет частные производныеи.

Доказательство. Поскольку функциядифференцируема, имеем представление. Пусть,. Тогда. Аналогично, если,, то. Так какА иВ конечны, тоитоже конечны, следовательно, существуют. Теорема доказана.

Поскольку полный дифференциал =, подставляяи, получим выражение дифференциала через частные производные:=. Отсюда приинаходими, поэтому=.

Аналогичное выражение имеет место и для функции любого числа переменных, т.е. если , то.

В случае функции одной переменной существования производной было достаточно для дифференцируемости функции. Для функции нескольких переменных ситуация другая: существования частных производных не достаточно для ее дифференцируемости. Имеет место

Теорема 3. Если существуют частные производные функции, непрерывные в точке, то в этой точке функция дифференцируема.

Доказательство. Поскольку, по условию, частные производные непрерывны в точке, они существуют в некоторой окрестности этой точки. Рассмотрим приращение данной функции при переходе из точкив точку, которая принадлежит указанной окрестности:

.

В первой квадратной скобке получилось приращение функции при переходе из точки в точку, при этом изменилась только одна переменнаях. Поэтому по формуле Лагранжа можно записать:

.

Аналогично, для второй квадратной скобки имеем:

.

Тогда полное приращение

.

В силу непрерывности частных производных в точке имеем:

,.

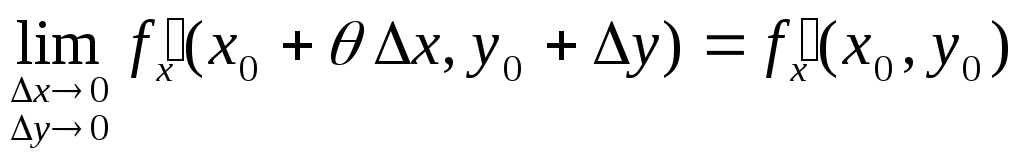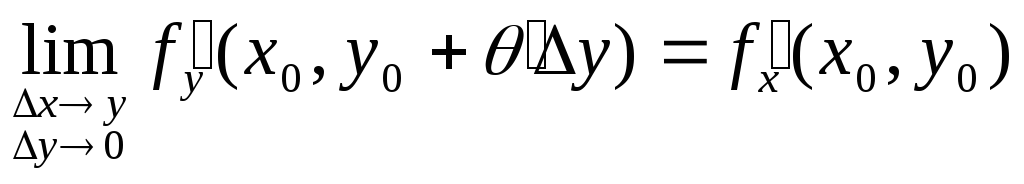Следовательно, прии,прии. Тогда

.

Таким образом, приращение представлено в виде (19.1), поэтому функциядифференцируема в точке. Теорема доказана.

Выведем теперь формулы для вычисления производных сложной функции нескольких переменных. Сначала рассмотрим случай дифференцируемой функции , аргументы которой зависят от одной переменнойt, т.е., причем функцииитоже дифференцируемы. Нужно найти производную. Пусть аргументt получает приращение. Тогдах иу получат соответствующие приращения,, причемиприв силу непрерывности дифференцируемой функции. Функциятоже получит приращениев силу ее дифференцируемости. Отсюда

,.

Таким образом,

. (19.1)

Заметим, что знак пишется тогда, когда находится частная производная функции по одной из нескольких переменных, знакd – тогда, когда производная находится по основному аргументу, и этот аргумент единственный.

Может получиться так, что у функции переменнаяу зависит отх, т.е.. Тогда основным аргументом являетсяхи формула (19.1) принимает вид

.

В случае, когда количество аргументов у функции z больше двух, но все они зависят от одного аргументаt, то получается формула, аналогичная формуле (19.1). Например, для функции, гдеимеем

. (19.2)

Теперь рассмотрим случай, когда основных аргументов два, а не один. Пусть . Здесь уже производные по основным аргументам будут частными производными (их два). Положими найдем, воспользовавшись формулой (19.1):

.

Аналогично,

.

В случае большего числа переменных формулы получаются аналогично.

Для функции одной переменной известно, что форма дифференциалаостается неизменной, если заменить независимую переменнуюх функцией. Имеет ли место это свойство для функции нескольких переменных? Выясним это.

Если , гдех иу – независимые переменные, то, как показано выше,

.

Пусть теперь х иу – функции,. Поскольку теперь ухеu иv – независимые переменные, имеем

.

(предполагаем, что для всех функций выполняются достаточные условия дифференцируемости). По правилу дифференцирования сложной функции

,,

поэтому

, т.е. формула для вычисления дифференциала сохраняется и в случае, когдах иу – функции. Таким образом, форма дифференциала является инвариантной, т.е. неизменной и для независимых переменныхх иу, и для функцийх иу.

Рассмотрим теперь частные производные и дифференциалы высших порядков. Пусть . Для функций большего числа переменных рассуждения аналогичны.

Частные производные ив свою очередь могут оказаться функциями двух переменных. Если от них снова найти частные производные, то они называются частными производными 2-го порядка и обозначаютсяпри этоминазываютсясмешанными производными. Например, для функции. Аналогично определяются частные производные 3-го, 4-го и т.д. порядка.

Видим, что в приведенном примере . Всегда ли так будет или это случайное совпадение? Имеет место

Теорема 4 (о равенстве смешанных производных). Если функция: 1) определена в открытой областиD; 2) в этой области существуют первые производныеи, а также вторые смешанные производныеи; 3) производныеинепрерывны в некоторой точкеобластиD, то

.

Доказательство. Рассмотрим вспомогательное выражение

, (19.3)

где h иk отличны от нуля и настолько малы, что вD содержится весь прямоугольник. Пусть– вспомогательная функция, дифференцируемая на отрезкев силу 2-го условия теоремы и, следовательно, непрерывная. Имеем. Выражение (19.3) с помощьюзаписывается следующим образом:

. (19.4)

С помощью формулы Лагранжа последнее равенство запишется в виде

.

Поскольку существует, по формуле Лагранжа поу получаем

.

Рассуждая аналогично, с помощью вспомогательной функции

из (19.3) получим , поэтому

=.

Переходя в последнем равенстве к пределу при ии учитывая, чтои смешанные производные непрерывны, получим

=.

Теорема доказана.

Пусть – функция двух независимых переменныхх иу, дифференцируемая в областиD. Тогда в этой области функция имеет полный дифференциал

,

где . Зафиксируеми. Тогда дифференциалявляется функцией только переменныхх иу, определенной в областиD. Полный дифференциал от дифференциаланазывается дифференциалом 2-го порядка или вторым дифференциалом функциии обозначаетсяили. Таким образом, по определению. Учитывая, чтоипостоянны, находим

.

Предполагая частные производные второго порядка непрерывными в области D, получим, что смешанные производные равны и

.

Аналогично, если в области Dфункцияимеет непрерывные частные производные 3-го порядка, то дифференциал от дифференциаланазывается ее дифференциалом 3-го порядка или третьим дифференциалом и вычисляется по формуле

,

и т.д.

Символически можно записать

,

,

.

Здесь правую часть нужно понимать так: двучлен в скобках возводится формально в соответствующую степень и результат почленно умножается на z, полученные произведения считаются производными соответствующих порядков.

Пример 2. Для функциинайдемв точке.

Решение. Найдем частные производные 3-го порядка данной функции, вычислим их в данной точке и подставим в формулу для. Имеем

и

.

В случае большего числа переменных формулы получаются аналогично. Например, для функции

.

Если переменные х иу не являются независимыми переменными, то (как и в случае функции одной переменной) форма записи дифференциалов высших порядков изменяется, т.е. дифференциалы высших порядков не обладают свойством инвариантности их формы. Например, для функции

.

Здесь уже х иу – функции, поэтомуи– функции, иине равны нулю.