§ 18. Понятие, предел и непрерывность функции нескольких переменных

Понятие функции нескольких переменных вводится с помощью понятия отображения множеств, которое было нами введено в 1 семестре.

Определение 1. ПустьХ – множество пар (х;у) действительных чисел. Отображениеf Х вR, сопоставляющее каждой паре чисел (х;у)число, называетсяфункцией двух переменных, заданной на множествеХ. При этомх иу называютсяаргументами функцииf,Х –областью ее определения,–значением функции. Множествоназываетсямножеством значений функции.

Аналогично определяется функция трех переменных и функцияnпеременных, если в качествеХ рассматривать множества системидействительных чисел соответственно.

Определение 2.Естественной областью определения функции нескольких переменных называется множество значений ее аргументов, при которых функция имеет смысл.

Пример 1. Найдем области определения функций,,.

Решение. Все три функции имеют смысл, когда подкоренные выражения неотрицательны, т.е.. В первом случае имеем– круг с центром в начале координат и радиусом 1, во втором –– шар с центром в начале координат и радиусом 1, в третьем случае–n-мерный шар с центром в начале координат и радиусом 1.

Для функции двух переменных можно построить график, т.е. множество всех точектрехмерного пространства, для которых, аz – значение функции в точке (х;у). Графиком обычно является некоторая поверхность. Например, графиком функцииявляется поверхность параболоида вращения, график функции– полусфера.

z

z

О

О х x

y y

При график функциипостроить невозможно.

Как известно, каждой точке плоскости с заданной декартовой системой координат соответствует единственная пара чисел – ее координат, и наоборот. Поэтому пары чисел и точки плоскости можно отождествлять и для пар чисел применять геометрическую терминологию, называя пару чисел (х;у) точкой плоскости. Аналогично, тройку чиселможно называть точкой трехмерного пространства.

Продолжая аналогию, назовем n-мерной точкой системуn действительных чисел:, а числаназовем координатами точкиМ. Множество всехn-мерных точек назовемn-мерным пространством. Обобщая известную формулу для расстояния между двумя точками плоскости, определим расстояние между точкамии n-мерного пространства формулой

. (18.1)

n-мерное пространство с введенным по формуле (18.1) расстоянием между любыми его двумя точками называетсяn-мерным евклидовым пространством . Приполучаем евклидову плоскость, при– трехмерное евклидово пространство.

В качестве окрестности точки n-мерного евклидова пространства будем рассматриватьn-мерный шар с центром в этой точке, т.е. множество всех точекпространства , координаты которых удовлетворяют неравенству

. (18.2)

Определение 3.Предельной точкой данного множестваЕточек пространства называется такая точка, в любой окрестности которой имеется хотя бы одна отличная отточкаМ этого множества.

Как и в случае множества одномерного пространства, т.е. множества числовой прямой, предельная точка может принадлежатьЕ и не принадлежатьЕ. Например, для множестваЕ всех точек плоскости вида, гдеm иn – любые натуральные числа, точка– предельная, не принадлежащая этому множеству. Если же множествоЕ =(прямоугольник), то все его предельные точки принадлежат этому множеству.

Определение 4. Непустоеn-мерное точечное множество называетсязамкнутым, если оно содержит все свои предельные точки.

Таким образом, множество не является замкнутым, а прямоугольникЕ =– замкнутое множество. Замкнутыми являются и все пространство и любое множество, не имеющее ни одной предельной точки (например, любое конечное множество точек).

Определение 5. ТочкаА данногоn-мерного множестваЕ называется еговнутренней точкой, если существует такая окрестность этой точки, которая целиком состоит из точек данного множества.n-мерное точечное множество называется открытым, если все его точки являются внутренними.

Например, круг – открытое множество, открытым множеством является и все пространство .

Определение 6. Пусть– предельная точка области определенияфункцииn переменных. Числоl называетсяпределом этой функции в точкеА, если для любогонайдется окрестность точкиА такая, что для всех точекэтой окрестности,, имеет место неравенство

, т.е..

Пишут: 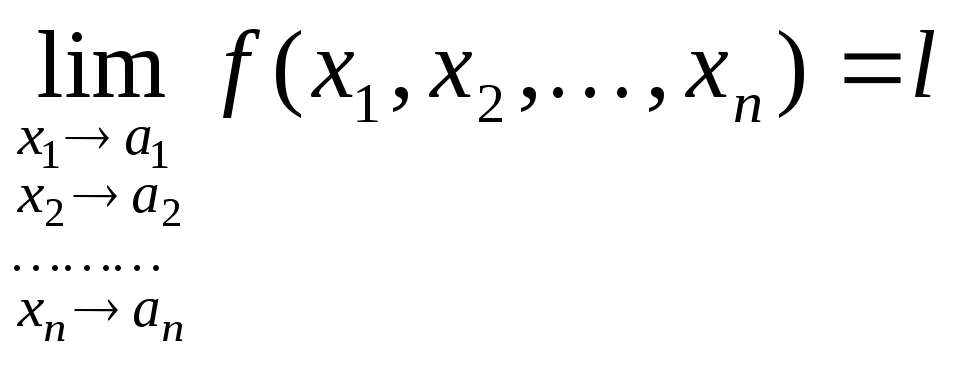или.

Можно дать и другое определение предела функции в точке (на языке последовательностей), равносильное данному определению.

Определение 7. Пусть– предельная точка области определенияфункции. Числоl называется пределом этой функции в точкеА, если для любой последовательности точек, принадлежащихи сходящихся кА, соответствующая последовательность значений функциисходится к числуl.

Второе определение особенно полезно при доказательстве того, что функция не имеет предела в данной точке. Для этого достаточно указать две последовательности точек, сходящихся к данной точке, такие, что соответствующие последовательности значений функции сходятся к разным пределам. Часто оказывается удобным брать последовательности точек на кривых, проходящих через предельную точку, причем при движении по кривой координаты могут изменяться и непрерывно.

Пример 2. Покажем, что функцияв точкене имеет предела.

Решение. Заметим, что через начало координатпроходит любая прямая вида, гдеk =const. Найдем предел функции, когда точкаприближается к точкеО по прямой. Имеем

.

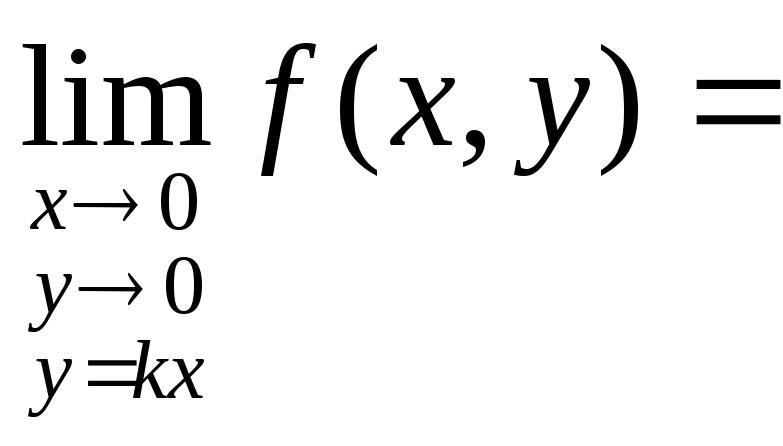
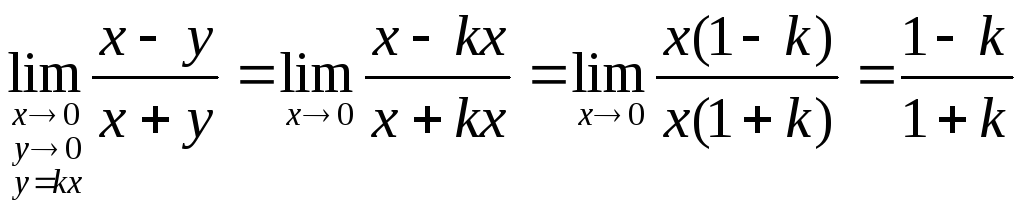Видим, что величина предела зависит от k, т.е. от пути движения к предельной точке. Поэтому предела нет.

Бесконечно малые и бесконечно большие функции, предел функции на бесконечности определяются аналогично случаю функции одной переменной.

При вычислении пределов функции нескольких переменных можно использовать замечательные пределы.

Пример 3.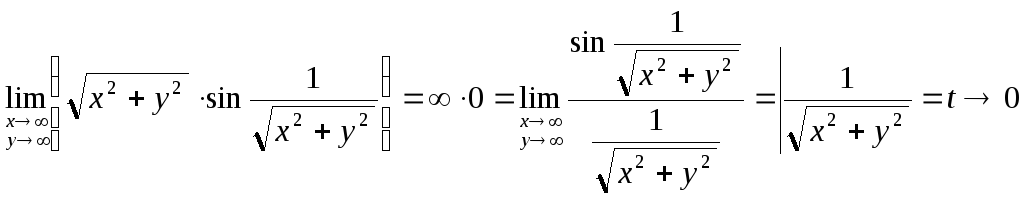прии.

На пределы функций нескольких переменных распространяются основные теоремы о пределах, доказанные нами для функций одной переменной: об ограниченности функции, имеющей предел, о пределе суммы, произведения и частного функций, леммы о бесконечно малых функциях и т.д. Доказательства их аналогичны приведенным в 1-м семестре.

Введем теперь понятие непрерывности функции нескольких переменных.

Определение 8. Функцияназываетсянепрерывной в точке, если имеет место равенство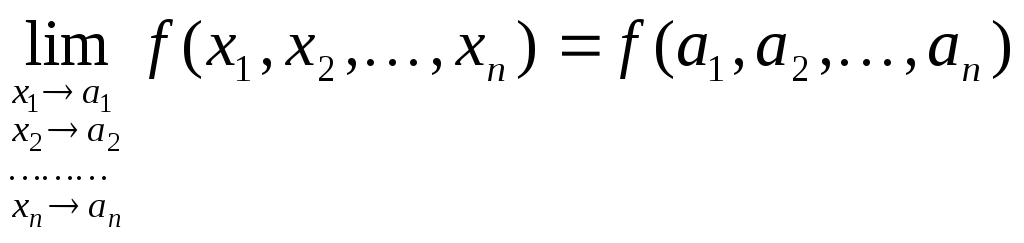, или,

короче, . В противном случае функция терпит разрыв в точкеА,А – точка разрыва функции.

Пример 4. Покажем, что функция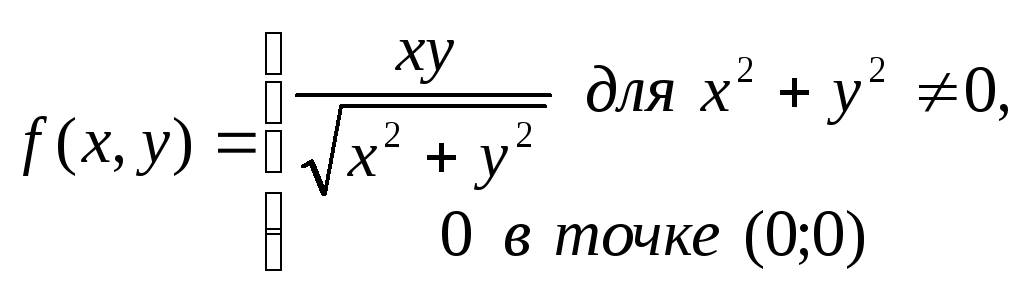непрерывна в каждой точке.

Решение. Для любой точки, отличной от точки, по теоремам о пределе функции имеем: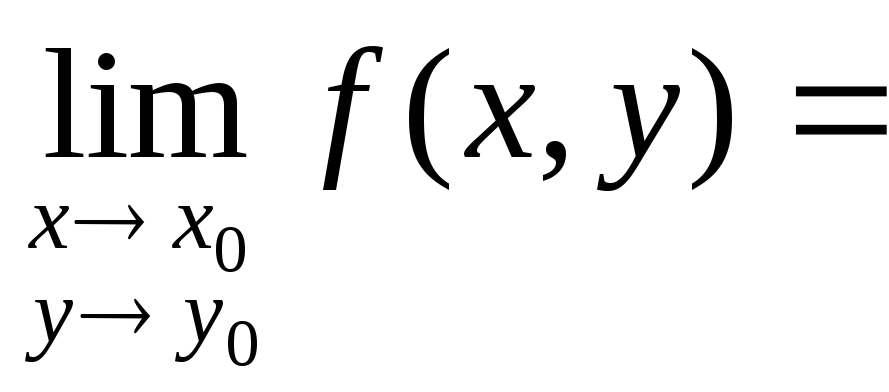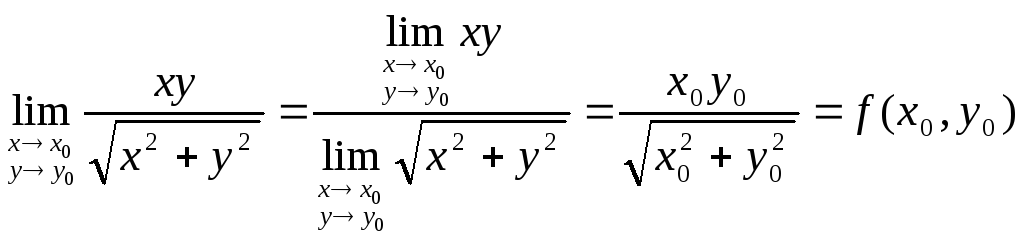, т.е. в этой точке функция непрерывна.

Для того, чтобы доказать непрерывность функции в точке , заметим, что

. Поскольку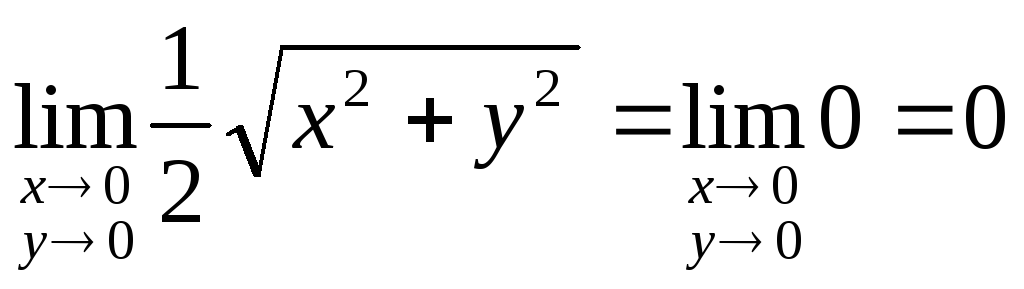, то и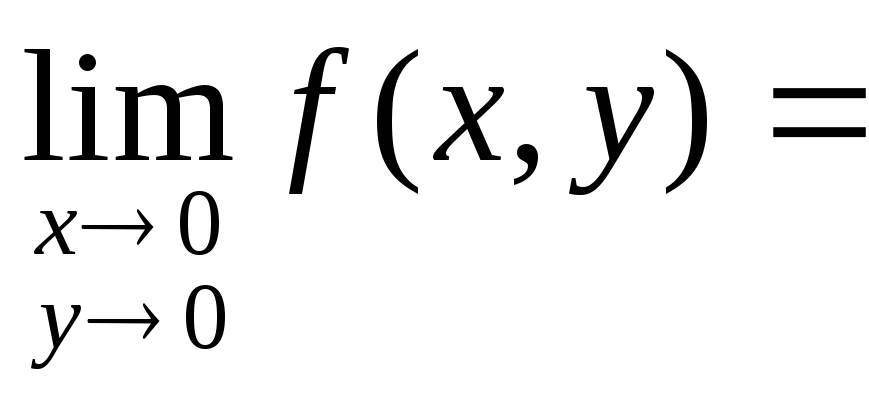=по теореме о промежуточной переменной, т.е. требуемое равенство выполнено.

Пример 5. Исследуем на непрерывность функцию

Решение. Так же, как в примере 4, с помощью теорем о пределе функции доказываем непрерывность функциив точке, отличной от точки. Для точкиимеем: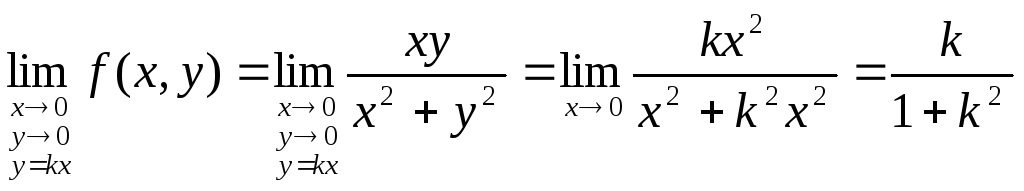– зависит отk, т.е. предел не существует, поэтому функция разрывна в этой точке.

Таким образом, функция непрерывна на множестве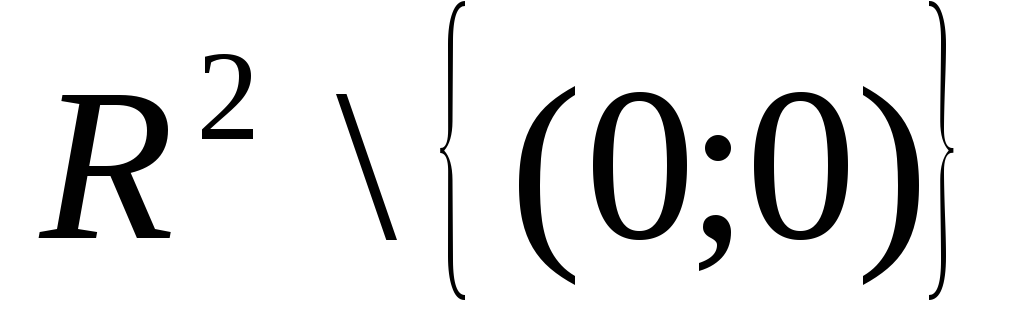и терпит разрыв в точке.

Пример 6. Исследуем на непрерывность функцию.

Решение. Так же, как в примерах 4 и 5, доказывается, что функциянепрерывна, если. Если, то функция терпит разрыв, так как в этих точках функция не определена, т.е. функция разрывна в точках прямой.

Для функций нескольких переменных имеет место ряд теорем, аналогичных соответствующим теоремам для функций одной переменной: теоремы о непрерывности суммы, произведения, частного непрерывных функций, сложной функции и т.д. Справедливы также теоремы, аналогичные теоремам Вейерштрасса и Больцано-Коши.