
- •§ 18. Понятие, предел и непрерывность функции нескольких переменных
- •§ 19. Частные производные и дифференциал функции нескольких переменных
- •§ 20. Экстремум функции нескольких переменных. Наибольшее и наименьшее значения функции в замкнутой области
- •§ 21. Касательная плоскость и нормаль к поверхности
- •§ 22. Производная по заданному направлению. Градиент
- •§ 23. Неявные функции, их дифференцирование
§ 20. Экстремум функции нескольких переменных. Наибольшее и наименьшее значения функции в замкнутой области
Определение 1. Точка![]() называетсяточкой максимума (точкой
минимума) функции
называетсяточкой максимума (точкой
минимума) функции![]() ,
если существует такая окрестность точки
,
если существует такая окрестность точки![]() ,
для всех точек
,
для всех точек![]() которой выполняется неравенство
которой выполняется неравенство
![]() или
или![]() (20.1)
(20.1)
(соответственно,
![]() или
или![]() .
.
Для функций большего числа переменных точки максимума и минимума определяются аналогично.
Точки максимума и минимума называются точками экстремума.
Теорема 1 (необходимое условие
экстремума). Если функция![]() имеет в точке
имеет в точке![]() конечные частные производные и эта
точка является точкой экстремума, то
обе частные производные в точке
конечные частные производные и эта
точка является точкой экстремума, то
обе частные производные в точке![]() равны нулю.
равны нулю.
Доказательство. Пусть функция![]() в точке
в точке![]() имеет максимум. Зафиксируем значение
имеет максимум. Зафиксируем значение![]() ,
тогда функция
,
тогда функция![]() будет функцией одной переменнойх,
для которой в некоторой окрестности
точки
будет функцией одной переменнойх,
для которой в некоторой окрестности
точки![]() выполняется неравенство
выполняется неравенство![]() ,
т.е.
,
т.е.![]() −
точка максимума функции одной переменной
−
точка максимума функции одной переменной![]() .
Тогда должно быть
.
Тогда должно быть![]() .
.
Аналогично показывается, что
![]() .
.
Теорема доказана.
Аналогичная теорема справедлива и для функции большего числа переменных.
Таким образом, экстремум может быть только в тех точках, в которых частные производные равны нулю или не существуют, т.е. в критических точках. Но не всякая критическая точка является точкой экстремума. Установим достаточные условия существования экстремума для функции двух переменных.
Теорема 2 (достаточные условия
экстремума). Если функция![]() в некоторой окрестности точки
в некоторой окрестности точки![]() имеет частные производные до второго
порядка включительно, причем
имеет частные производные до второго
порядка включительно, причем![]() ,
,![]() ,
а вторые частные производные непрерывны
в точке
,
а вторые частные производные непрерывны
в точке![]() ,
то функция
,
то функция![]() в этой точке:
в этой точке:
1) при
![]() имеет максимум, если
имеет максимум, если![]() и минимум, если
и минимум, если![]() ;
;
2) при
![]() не имеет экстремума.
не имеет экстремума.
Без доказательства.
Таким образом, для отыскания точек
экстремума функции двух переменных
![]() нужно
вычислить ее частные производные, из
системы уравнений
нужно
вычислить ее частные производные, из
системы уравнений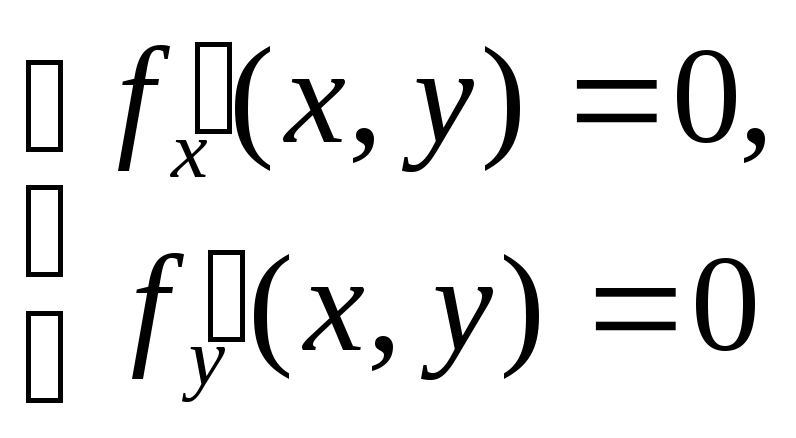 найти стационарные точки, вычислить
значения вторых производных в этих
точках и проверить знак
найти стационарные точки, вычислить
значения вторых производных в этих
точках и проверить знак![]() .
Если
.
Если![]() ,
то при
,
то при![]() в стационарной точке – минимум функции,
при
в стационарной точке – минимум функции,
при![]() − максимум. Если
− максимум. Если![]() ,
то стационарная точка не является точкой
экстремума. Если
,
то стационарная точка не является точкой
экстремума. Если![]() ,
то исследовать стационарную точку на
экстремум нужно с помощью производных
высших порядков.
,
то исследовать стационарную точку на
экстремум нужно с помощью производных
высших порядков.
Пример 1. Исследуем на экстремум
функцию![]() .
.
Решение. Имеем![]() ,
,![]() ,
,![]()
![]() т.е. стационарная точка одна:
т.е. стационарная точка одна:![]() .
Поскольку
.
Поскольку![]()
![]() ,
то
,
то![]() –
точка экстремума функции, причем в этой
точке функция имеет максимум, так как
–
точка экстремума функции, причем в этой
точке функция имеет максимум, так как![]() ,
,![]() .
.
Пусть теперь функция
![]() определена
и непрерывна в замкнутой ограниченной
областиD. Тогда по
теореме Вейерштрасса она принимает в
какой-то точке
определена
и непрерывна в замкнутой ограниченной
областиD. Тогда по
теореме Вейерштрасса она принимает в
какой-то точке![]() области наибольшее значение и в точке
области наибольшее значение и в точке![]() –
наименьшее значение. Если
–
наименьшее значение. Если![]() или
или![]() (или обе точки) – внутренние, то они
являются точками экстремума функции.
Кроме того, наибольшее (наименьшее)
значение функция может принимать и на
границе областиD.
(или обе точки) – внутренние, то они
являются точками экстремума функции.
Кроме того, наибольшее (наименьшее)
значение функция может принимать и на
границе областиD.
Таким образом, нужно найти значения функции в критических точках и сравнить их со значениями функции на границе D. Наибольшее (наименьшее) из полученных значений и будет наибольшим (наименьшим) значением функции в замкнутой областиD.
Пример 2. Найдем наибольшее и
наименьшее значения функции![]() в треугольнике
в треугольнике![]() ,
ограниченном сторонами
,
ограниченном сторонами![]() .
.
Р
3 А
критические точки функции. Имеем



![]() ,
,![]() .
Частные производные существуют в каждой
точке, поэтому достаточно найти
стационарные точки функции,
.
Частные производные существуют в каждой
точке, поэтому достаточно найти
стационарные точки функции,
у
(D)
В
О
3
х
т.е. решить систему уравнений

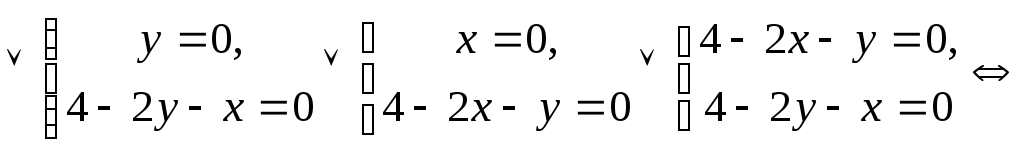
![]()
![]() .
Внутри области лежит лишь точка
.
Внутри области лежит лишь точка![]() (так как на сторонеАВ находится
точка
(так как на сторонеАВ находится
точка![]() ),
которая и является стационарной точкой
функции.
),
которая и является стационарной точкой
функции.
![]() .
.
Изучим поведение функции на границе
треугольника. На сторонах ОА иОВ,
очевидно,
![]() ,
на сторонеАВ
,
на сторонеАВ
![]() ,
поэтому
,
поэтому![]()
![]() ,
,
![]() .
Из подчеркнутых значений функции
выбираем наибольшее и наименьшее
значения:
.
Из подчеркнутых значений функции
выбираем наибольшее и наименьшее
значения:![]() ,
,![]() .
.
