
- •Теория вероятностей
- •Содержание
- •Введение
- •Часть 1. Случайные события
- •Комбинаторика
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •2 Классическое, статистическое и геометрическое определение вероятности события. Непосредственный подсчет вероятности
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •3 Теоремы сложения и умножения вероятностей
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •4 Полная вероятность. Формулы Байеса (Бейеса)
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •5 Повторные независимые испытания
- •5.1 Основные формулы
- •5.2 Наивероятнейшее число появлений события в независимых испытаниях
- •5.3 Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •Часть 2. Случайные величины
- •1 Дискретные случайные величины
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •2 Непрерывные случайные величины
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •3 Частные виды распределений непрерывных случайных величин
- •Нормальное распределение
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •3.2 Показательное распределение
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •3.3 Равномерное распределение
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •Закон больших чисел
- •Задачи для аудиторного решения
- •Задачи для самостоятельного решения
- •5 Цепи Маркова
- •Задачи для самостоятельного решения
- •Список использованной литературы
- •Приложения
- •Задачи для подготовки к контрольной работе №1
- •Задачи для подготовки к контрольной работе №2
- •Дополнительные задачи по курсу теории вероятностей
- •Тесты по теории вероятностей Вариант 0
- •Вариант 1
- •Вариант 2
- •Вопросы для подготовки к экзамену по теории вероятностей
- •Теория вероятностей
- •426069, Г. Ижевск, ул. Студенческая, 11.
Задачи для аудиторного решения
Функция плотности равномерного распределения изображена на рисунке 32.
1) Найти параметр С и записать аналитическое выражение функции плотности .
2) Записать функцию распределения и построить ее график.
3) Найти вероятность, что непрерывная случайная величина Х примет отрицательное значение.
4) Найти математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины Х.
 у
у
![]()
С 0 5 х
Рисунок 32
Функция распределения равномерно распределенной непрерывной случайной величины Х имеет вид
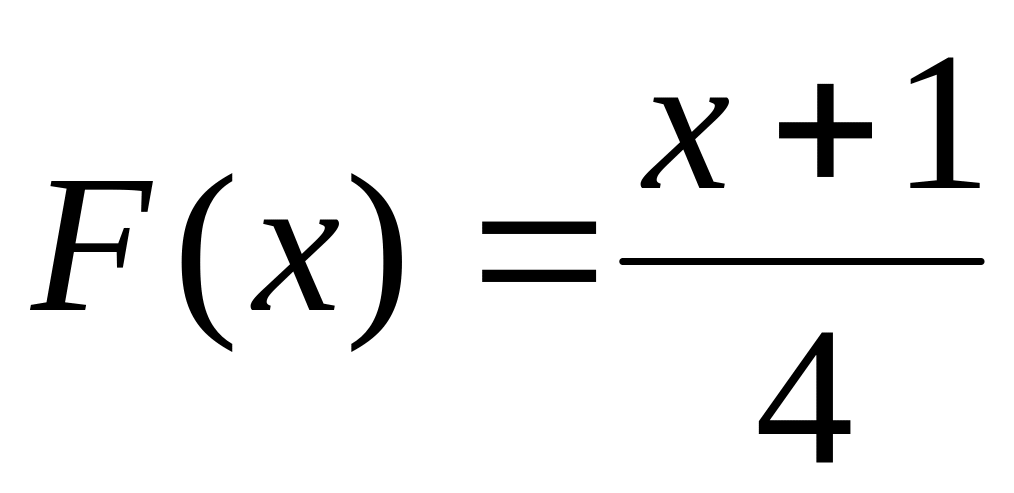 ,
где
,
где
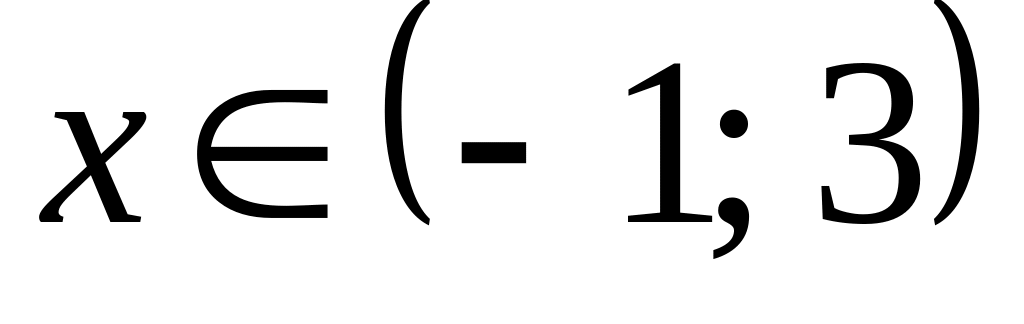 .
.
1) Построить график функции .
2) Найти функцию плотности и построить ее график.
3) Найти вероятность,
что в 500 независимых испытаниях случайная
величина Х
не менее 150 раз попадет в интервал
![]() .
.
Случайные величины Х и Y независимы и распределены равномерно: Х в интервале
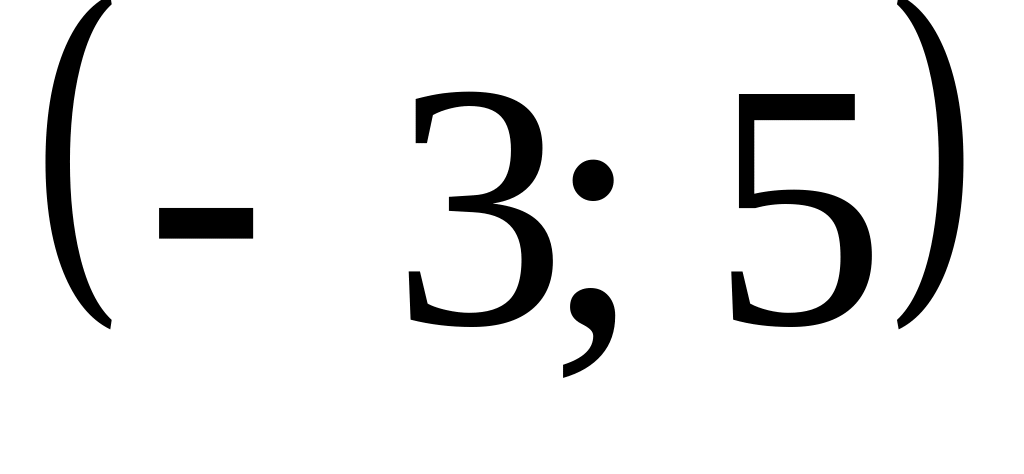 ,
Y
– в интервале
,
Y
– в интервале
 .
Найти дисперсию суммы Х
и Y.
.
Найти дисперсию суммы Х
и Y.
Задачи для самостоятельного решения
Функция распределения равномерного распределения имеет вид:
![]()
1) Найти параметр С.
2) Построить график .
3) Записать функцию плотности и построить ее график.
4) Найти вероятность того, что непрерывная случайная величина Х примет значение, не меньшее –3.
Функция плотности равномерного распределения изображена на рисунке 33. Найти математическое ожидание непрерывной случайной величины Х.
 у
у



 5
5


0 2 С х
Рисунок 33
Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир входит на платформу в случайный момент времени. Какова вероятность, что ждать пассажиру придется не больше полминуты. Найти среднее время ожидания и среднее квадратическое отклонение времени ожидания поезда.
Случайные величины Х и Y независимы и распределены равномерно: Х в интервале
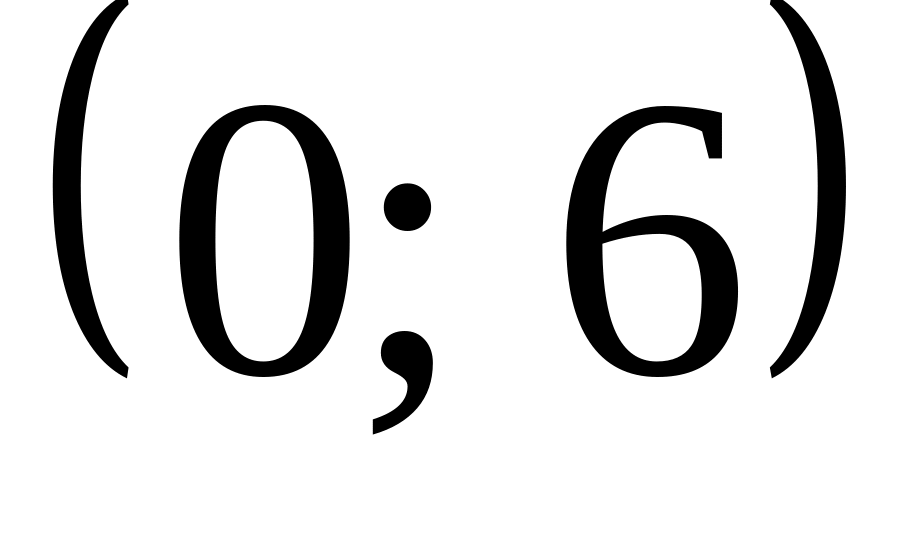 ,
Y
– в интервале
,
Y
– в интервале
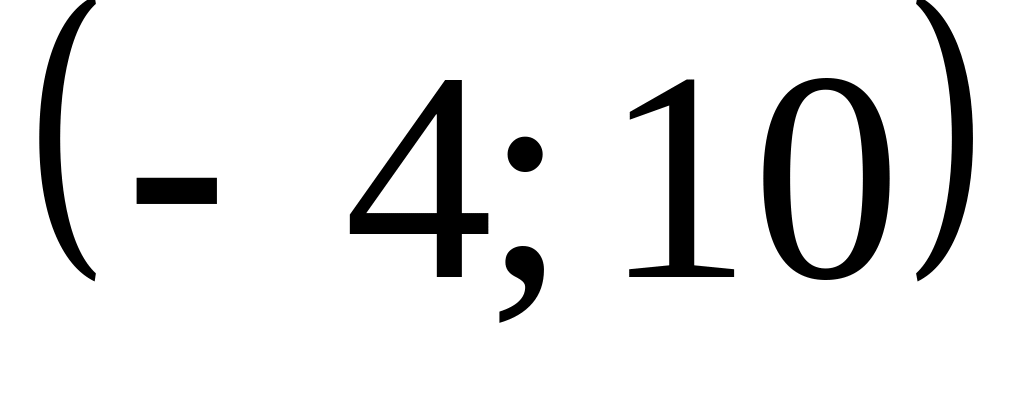 .
Найти
.
Найти
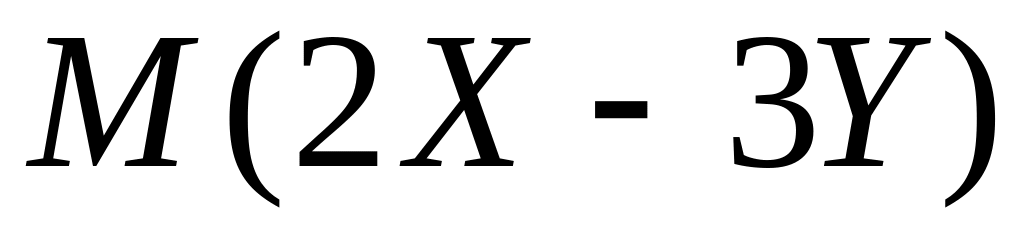 .
.Непрерывная случайная величина Х имеет равномерное распределение с математическим ожидание и дисперсией
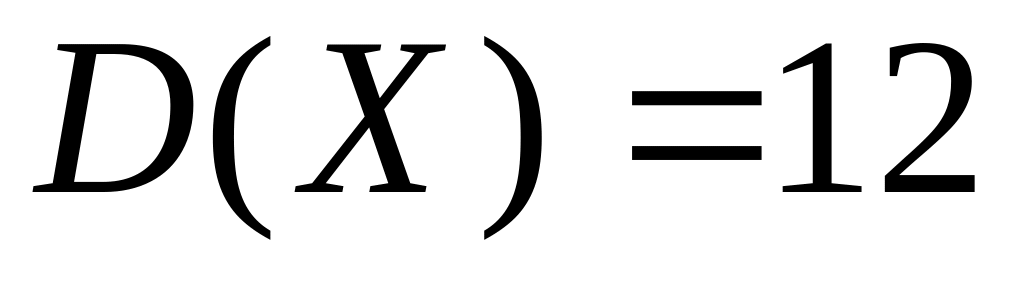 .
Написать функцию плотности
.
.
Написать функцию плотности
.
Закон больших чисел
Установлено, что при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности. Под законом больших чисел понимается ряд математических теорем (теорема Чебышева, теорема Пуассона, теорема Бернулли), в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным. В основе доказательств этих теорем используются неравенства Маркова и Чебышева.
Теорема (неравенство Маркова). Если случайная величина Х принимает только неотрицательные значения и имеет конечное математическое ожидание, то для любого положительного числа верно неравенство
![]() .
.
Теорема (неравенство Чебышева). Для любой случайной величины, имеющей конечное математическое ожидание и дисперсию, справедливо неравенство
![]() .
.
Теорема
Чебышева. Если
случайные величины
![]() независимы, имеют математические
ожидания
независимы, имеют математические
ожидания
![]() и дисперсии
и дисперсии
![]() ,
ограниченные одним и тем же числом С,
то для любого числа
,
ограниченные одним и тем же числом С,
то для любого числа
![]() выполняется неравенство
выполняется неравенство
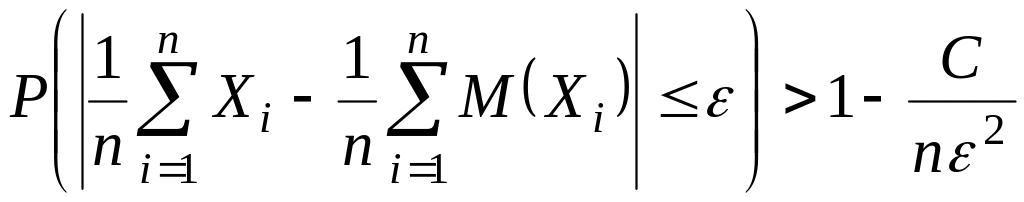 .
.
Отсюда следует, что
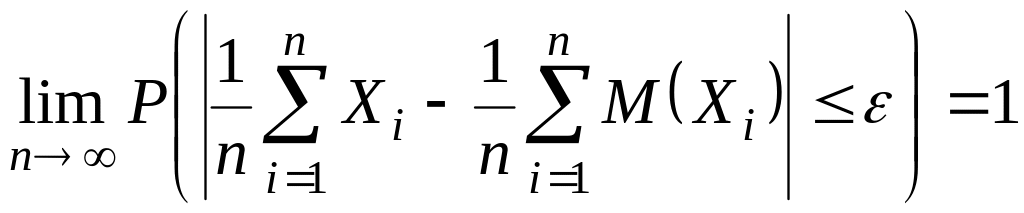 .
.
Если все случайные
величины
![]() (
(![]() 2, 3, …, п)
имеют одно и то же математическое
ожидание
2, 3, …, п)
имеют одно и то же математическое
ожидание
![]() (
2, 3, …, п),
то неравенство принимает вид
(
2, 3, …, п),
то неравенство принимает вид
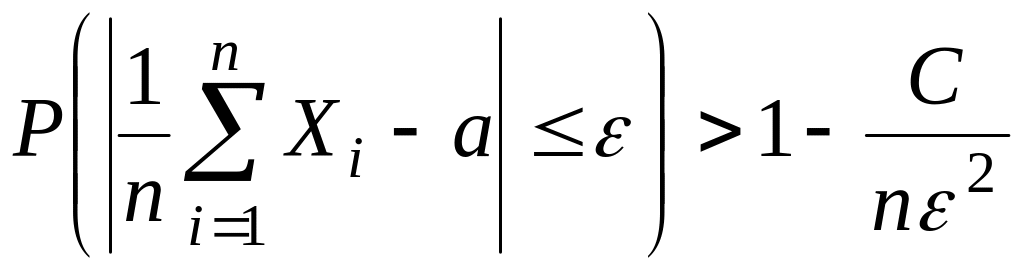 .
.
Переходя к пределу
при
![]() ,
отсюда получают
,
отсюда получают
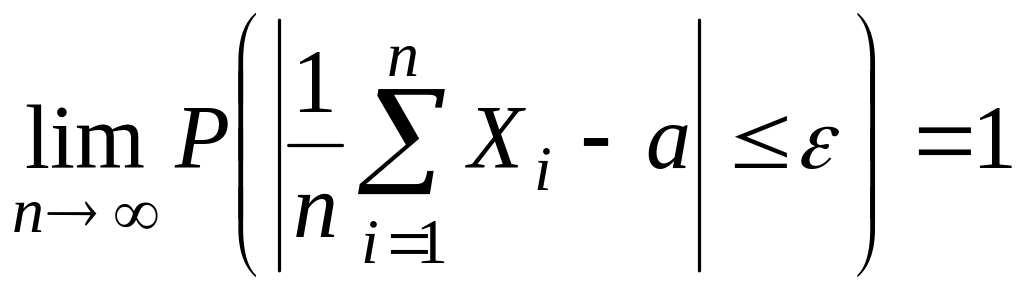 .
.
Теорема
Бернулли. Если
в каждом из п независимых испытаний
вероятность р появления события А
постоянна, то вероятность того, что
отклонение частоты
![]() от
вероятности р по модулю не превзойдет
числа
,
больше, чем разность
от
вероятности р по модулю не превзойдет
числа
,
больше, чем разность
![]() ,
то есть
,
то есть
![]() .
.
Отсюда следует, что
![]() .
.
Пример 1. Средний срок службы мотора 4 года. Оценить снизу, что данный мотор не прослужит более 20 лет.
Решение. Введем
случайную величину Х
– срок службы мотора. Из условия задачи
следует, что
![]() .
Для оценки вероятности используем
неравенство Маркова
:
.
Для оценки вероятности используем
неравенство Маркова
:
![]() .
.
Таким образом, вероятность того, что мотор прослужит более 20 лет, превышает 0,8.
Пример 2. Сумма всех вкладов в некотором сберегательном банке составляет 2 млн. руб., а вероятность того, что случайно взятый вклад не превышает 10000 руб., равна 0,8. Что можно сказать о числе вкладчиков данного сберегательного банка?
Решение. Пусть
случайная величина Х
– величина случайно взятого вклада, а
п
– число всех вкладчиков. Тогда средняя
величина вклада
![]() ,
а
,
а
![]() .
Используя неравенство Маркова, получаем
.
Используя неравенство Маркова, получаем
![]() ,
,
или
![]() .
.
Отсюда

то есть число вкладчиков данного сберегательного банка не превышает 1000.
Пример 3. Электростанция обслуживает сеть из 18000 ламп, вероятность включения каждой из которых в зимний вечер равна 0,9. Определить вероятность того, что число ламп, включенных в сеть зимним вечером, отличается от своего математического ожидания по абсолютной величине не более чем на 200.
Решение. Так как число включенных ламп – это случайная величина, распределенная по биномиальному закону, то
![]() ,
,
![]() .
.
Определим искомую вероятность, используя неравенство Чебышева :
![]() .
.
Пример 4. Оценить вероятность того, что отклонение любой случайной величины от ее математического ожидания по модулю будет меньше трех средних квадратических отклонений этой величины.
Решение. Оценим
вероятность, используя неравенство
Чебышева. Так как по условию задачи
![]() ,
а
,
а
![]() ,
то
,
то
![]() .
.
Знаем, что в случае нормального распределения эта вероятность равна 0,9973, что не противоречит полученному результату.
Пример 5. Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было взято на выборку по одной лампе из каждого ящика. Оценить вероятность того, что средняя продолжительность горения отобранных 200 электроламп отличается от средней продолжительности горения во всей партии по абсолютной величине меньше, чем на 5 часов, если известно, что среднее квадратическое отклонение продолжительности горения любой лампы в каждом ящике меньше 7 часов.
Решение. Введем
случайные величины
– продолжительность горения электролампы,
взятой из i-го
ящика. По условию задачи известно, что
дисперсия
![]() .
Очевидно, что средняя продолжительность
горения ламп в выборке
.
Очевидно, что средняя продолжительность
горения ламп в выборке
![]() ,
а средняя продолжительность горения
ламп во всей партии
,
а средняя продолжительность горения
ламп во всей партии
![]() .
Оценим искомую вероятность, используя
теорему Чебышева:
.
Оценим искомую вероятность, используя
теорему Чебышева:
.
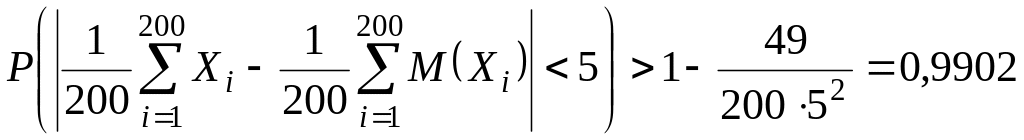 .
.
Пример 6. Пусть вероятность того, что покупателю обувного магазина необходима обувь 45 размера, равна 0,15. Оценить границы числа покупателей среди 2000 побывавших в магазине, которым нужна такая обувь, если эти границы надо гарантировать с вероятностью 0,98.
Решение. Если т – число покупателей, которым нужна обувь 45-го размера, то используем теорему Бернулли:
,
![]() ,
,
отсюда
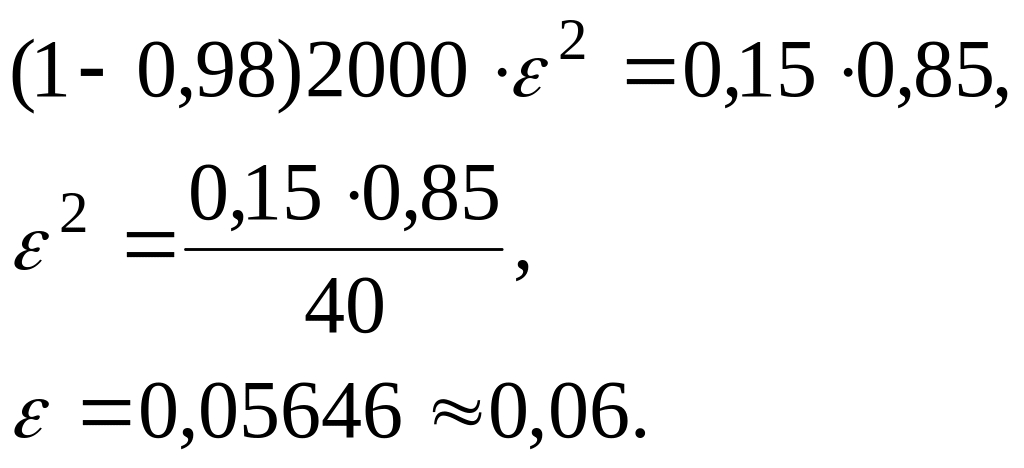
Тогда
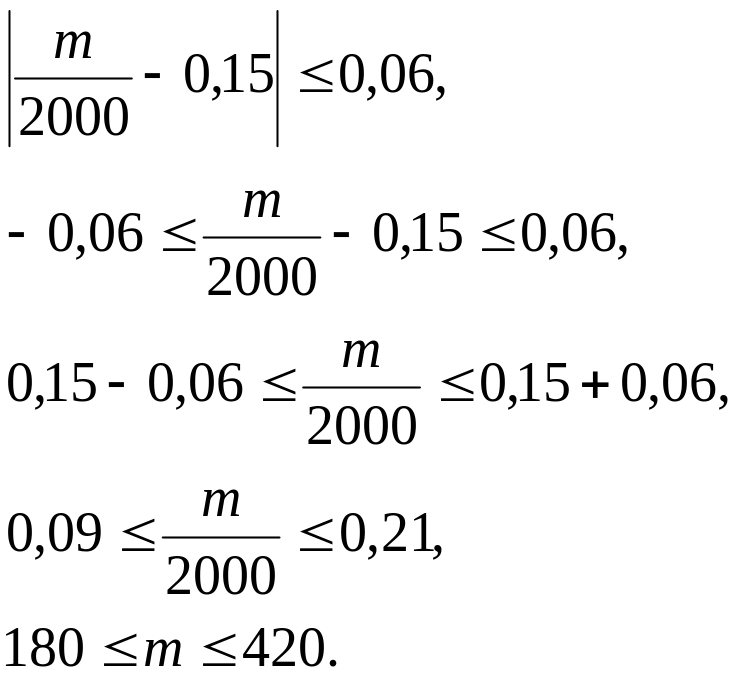 ,
,
Таким образом, можно гарантировать с вероятностью 0,98, что из 2000 покупателей, побывавших в магазине, число покупателей, которым нужна обувь 45 размера, заключено в границах от 180 до 420.
