3.6. Геометрический расчет сопла.

Геометрический расчет сопла заключается в определении длин входной части и выходной части .

, (3.10)

м.

, (3.11)

м.

34

3.7. Результаты газодинамического и геометрического расчетов сопла Лаваля.

Таблица 6.

	P, МПа	ρ,	T, K	W,	a,	λ	M	F, м2	d, м
Вход	6,79	32,8	697,74	114	538,2	0,231	0,212		0,047
Сеч. А	5,6	28,64	660,9	299	523,78	0,606	0,571		0,0309
Сеч. В	4,662	25,09	626,83	400	510,1	0,811	0,784		0,0285
Критика	3,7	21,26	586,7	493,5	493,5	1	1		0,0279
Сеч. C	1,062	8,72	410,4	780	412,74	1,581	1,89		0,0346
Сеч. D	0,0823	1,395	197,34	1025	286,21	2,078	3,58		0,0755
Выход	0,0001	0,0107	28,16	1179,2	108,12	2,4	10,91	0,507	0,804

35

4. Кинематический анализ движения жидкости.

Виды движения жидкой частицы. Кинематика жидкой среды существенно отличается от кинематики системы материальных то­чек или кинематики твердого тела. Движение твердого тела в об­щем случае складывается из поступательного перемещения вместе с полюсом (мгновенным центром вращения) и вращения относи­тельно мгновенной оси, Проходящей через полюс. Движение жидко­сти значительно сложнее, поскольку частица кроме указанных пе­ремещений может деформироваться.

Изучим возможные формы движения жидкой частицы, рассмат­ривая для начала ради простоты плоское движение в плоскости ху. Будем обозначать составляющие вектора скорости в данной точке через w_x, w_y, w_z. Для рассматриваемого плоского течения w_z = 0. Пусть частица в форме квадрата с «полюсом» в точке А перемести­лась за некоторое время А' в соседнее положение, изображенное на рис. 4.1 параллелограммом. Точка А при этом заняла положение А'. Очевидно, перемещение части складывается из следующих со­ставляющих: а) перемещение полюса; б) вращение около полюса; в) деформация частицы.

Скорость поступательного движения полюса, как и в случае движения твердого тела, определяется компонентами вектора ско­рости w_x, w_y

Вращательное движение жидкой частицы существенно отличается от вращения твердого тела. Действительно, вращение жид­кой частицы нельзя охарактеризовать угловой скоростью какого-либо одного отрезка, выбранного в этой частице. Например, угловая скорость w ребра АВ может быть определена из разности скоростей изменения составляющих скорости в направлении оси у:

.

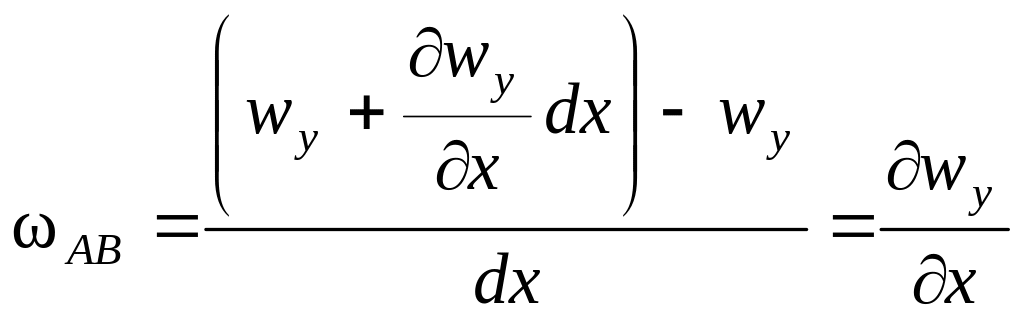Угловая скорость ребра AD равна

.

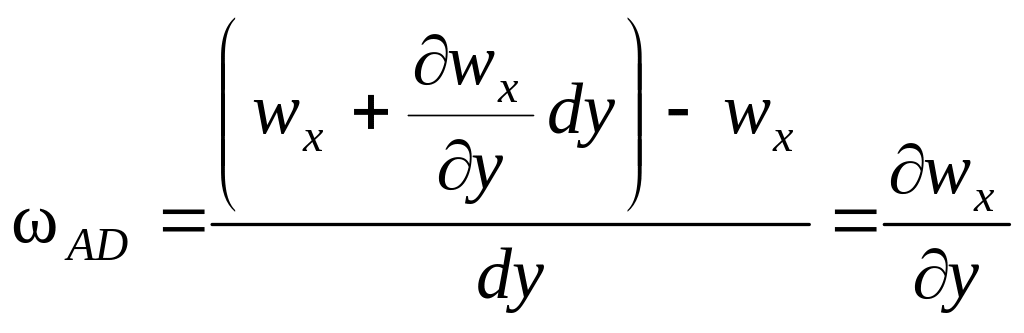По предложению Гельмгольца, за угловую скорость жидкой ча­стицы принимается средняя алгебраическая величина из угловых скоростей сторон прямоугольника

. (4. 1)

Индекс z в выражении (4. 1) показывает, что определяется состав­ляющая вектора угловой скорости относительно оси z, нормаль­ной к плоскости ху. Угловая скорость считается положительной, если вращение происходит против часовой стрелки.

36

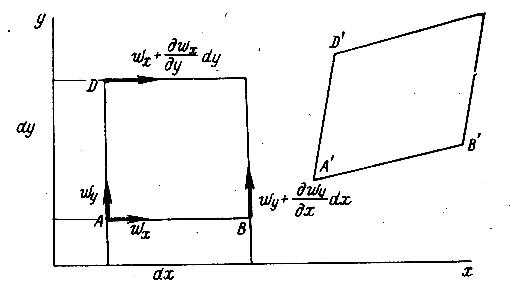
Рис.4.1

Деформация жидкой частицы может быть двоякого рода. Во-первых, это деформация растяжения-сжатия, характе­ризующаяся удлинением сторон исходной частицы. Очевидно, что такое удлинение определяется изменением соответствующих ком­понент скорости по координатным осям:

, .

Во-вторых, возможна деформация скоса ребер жидкой частицы, т. е. заострение (или затупление) исходных углов. Такую деформа­цию можно охарактеризовать поперечной изменчивостью скорости течения, или средней арифметической из угловых скоростей вращения ребер:

.

Приведенные соображения позволяют сформулировать тео­рему Гельмгольца: скорость жидкой частицы склады­вается из скорости полюса, скорости вращательного движения около оси, проходящей через полюс, и скорости деформационного движе­ния, состоящего в свою очередь из линейной деформации растяже­ния-сжатия и угловой деформации скашивания ребер частицы.

Теорема Гельмгольца справедлива и для более общего случая пространственного движения. При этом появляются новые члены, характеризующие движение: деформация растяжения – сжатия в на правлении оси z, т. е. , и угловые скорости и деформации скоса относительно осей у и х. Приведем выражения для этих величин без вывода. Угловые скорости:

, ,

(4.2)

37

деформации скоса:

, ,

. (4.3)

Индексы х, у, z при ε в последних выражениях не следует понимать как символы проекции: они указывают лишь направление перпен­дикуляра к площадке, в которой происходит перекашивание грани. Вообще в отличие от угловой скорости w, которая, как и в меха­нике твердого тела, имеет векторный характер, деформация скоса ε является скаляром.

Вихревое и безвихревое движение. Если при движении жидкости ее частицы вращаются и составляющие угловой скорости ω_x, ω_y, ω_z не равны нулю, движение называется вихревым. Наличие вращательных движений в двухмерном потоке может быть установ­лено таким простейшим экспериментом: в поток вводят поплавок со стрелкой-индикатором, причем его размер мал по сравнению с радиусом кривизны линий тока. Если при движении поплавка стрелка-индикатор не остается параллельной самой по себе, а из­меняет свое направление с некоторой угловой скоростью w, то дви­жение — вихревое и угловая скорость поплавка совпадает с угло­вой скоростью жидкой частицы.

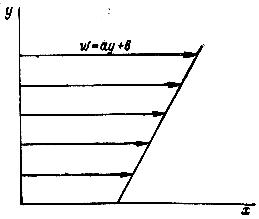
Необходимо отметить, что вихревым может быть течение и при прямолинейных траекториях частиц. Например, если частицы дви­жутся параллельно оси x (рис. 4.2), причем скорости изменяются по закону w_x = ay + b, где а и b — постоянные, то угловая ско­рость равна

;

Мы имеем вихревое течение, и поплавок, помещенный в поток, будет вращаться по часовой стрелке. Течение вязкой жидкости в трубах постоянного сечения — также вихревое, причем угловая скорость вращения частиц нарастает с приближением к стенке трубы.

Рассмотрим один частный случай движения жидкости, когда вращение частиц отсутствует. В этом случае ω_x = ω_y = ω_z = 0. Такое движение называется безвихревым.

Важность этого частного случая движения определяется тем обстоятельством, что, как показывает опыт, при обтекании тела с плавными обводами вращение частиц наблюдается только в тон­кой пристенной области и за кормой. Во всем остальном потоке движение осуществляется практически без вращения частиц. Поэ­тому безвихревое движение имеет особое значение для теории удобообтекаемых тел (таких, как современные самолеты, ракеты, ко­рабли, проточные части турбомашин). Особенно большое значение имеет теория безвихревого движения для решения за­дачи о распределении давлений на по­верхность обтекаемого тела.

38

Рис. 4.2. Движение частицы параллельно оси x.

При плоском (двухмерном) течении равенство нулю угловой скорости вра­щения приводит к выражению:

.

Если обратиться к рис. 4.1, то угловая скорость ребра АВ при этом будет и положительна (ребро АВ вращается против часовой стрелки). Угловая скорость ребра AD будет и отрицательна (ребро AD вращается по часовой стрелке). Средняя скорость вращения:

,

равная угловой скорости биссектрисы исходного прямого угла, в случае безвихревого движения равна нулю; частица перемещается без вращения, несмотря на наличие деформационного движения. В этом случае поплавок, опущенный в жидкость, будет переме­щаться вместе с потоком таким образом, что стрелка-индикатор остается все время параллельной самой себе.

Безвихревое циркуляционное течение. Интересным и практи­чески важным примером безвихревого движения является круго­вое течение, в котором скорость обратно пропорциональна расстоя­нию от оси вращения частиц (рис. 4.3):

. (4.4)

Хотя линии тока этого течения криволинейны, но поток является безвихревым — частицы деформируются, но не вращаются.

Течение, в котором скорость подчиняется закону (4.4), называют безвихревым циркуляционным потоком (иногда – менее точно – плоским вихрем).

Рассмотрим безвихревое циркуляционное течение с непрерывно убывающим радиусом. Скорость течения и ее градиент вблизи оси вращения должны непрерывно нарастать и в пределе стать беско­нечно большими (рис. 4.3). В реальной жидкости это невозможно из-за действия вязкости; опыт показывает, что центральная область вихря приходит во вращение и вращается как твердое тело с угло­вой скоростью ω. За пределами этого ядра вихря (заштрихованный круг на рис. 4.3) скорость изменяется по закону (4.4).

39

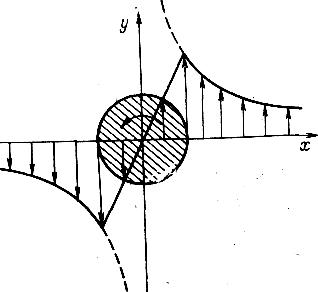
Рис. 4.3 Круговое течение

Приме­рами подобных потоков являются круговые течения у отверстия стока воды в ванне, атмосферные смерчи и т. д. Возрастание ско­рости с приближением к оси потока приводит к понижению давле­ния, поэтому свободная поверх­ность жидкости принимает воронко­образную форму. В свою очередь, и местное понижение давления в жидкости приводит через неко­торое время к формированию та­кого поля скоростей, которое при­ближается к безвихревому цирку­ляционному течению.

Важным примером использова­ния в технике безвихревого цир­куляционного течения является движение газов в спиральной ка­мере с тангенциальным подводом газа (рис. 4.4). Газовый поток вра­щается в камере; выход газов осу­ществляется через окна прорезан­ные в торцевых стенках камеры вблизи от ее оси. Хотя линии тока являются спиралями, но радиусы их кривизны приближенно можно считать равными радиусу соответствующей окружности r, прове­денному из оси камеры. Распределение скоро­стей оказывается близким к заданному форму­лой (4.4). Скорость сильно возрастает с при­ближением к оси камеры.

Возрастание скорости с приближением к оси спиральной камеры позволяет использо­вать ее в качестве циклонной уста­новки для сепарации твердых частиц из газо­вого потока — центробежные силы; действую­щие на частицы при движении с большой скоростью по криволинейным траекториям, отбрасывают их к стенкам камеры.

Другое применение спиральной камеры — так называемые ре­циркуляционные печи, используемые при термической обработке крупных поковок или отливок. Обрабатываемое изделие (садка) размещается у оси камеры. За счет большой скорости газов, обте­кающих поверхность садки, происходит интенсивный теплообмен между потоком и поверхностью, что позволяет сократить сроки термообработки.

40

Рис. 4.4. Движение газов в спиральной камере с тангенсиальным подводом газа.

41

Замечания руководителя

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ГОУВПО «ВГТУ»)

Авиационный факультет

Кафедра Теоретической и Промышленной теплоэнергетики

КУРСОВАЯ РАБОТА

по дисциплине «Гидрогазодинамика»

Расчетно-пояснительная записка

Разработал студент ____________________________________Д.И. Новиков

Подпись, дата Инициалы, фамилия

Руководитель_________________________________________________А.В. Муравьев

Подпись, дата Инициалы, фамилия

Члены комиссии ______________________________________________

Подпись, дата Инициалы, фамилия

Нормоконтролер _____________________________________________А.В. Муравьев

Подпись, дата Инициалы, фамилия

Защищена_______________________Оценка____________________________

дата

2008