Типовые цифровые последовательности
Графическое отображение цифровых последовательностей цифровых испытательных сигналов имеет ряд особенностей. Код цифрового сигнала изображается вертикальной линией, длина корой числовому выражению сигнала. Способ кодирования квантованных дискретных выборок и конкретный вид кодовых посылок не учитывается. Для того, чтобы подчеркнуть, что последовательность кодовых посылок изображает цифровой сигнал концы отображающих отрезков завершаются кружочками, рис.7.а.
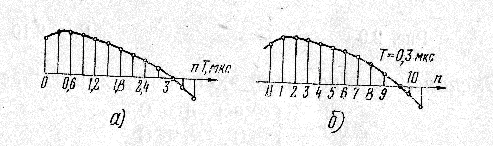
рис.7.
Несмотря на то,
что вообще говоря , цифровая
последовательность является функцией
непрерывного времени, ее отсчеты
определены в дискретные моменты времени
.
Если задать интервал дискретизации
в виде параметра, то цифровую
последовательность можно задать в виде
функции номера
ее
посылок, рис.7б.
Далее рассмотрим примеры типовых цифровых последовательностей.
1.Единичный импульс. Эта цифровая функция является одним из видов испытательных воздействий, с ее помощью определяется импульсная характеристика цифрового фильтра.
График цифрового импульса приведен ниже, на рис 8
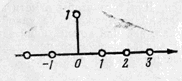
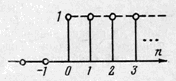
Рис.8 рис.9
2.Единичная функция
Выражение для единичной функции имеет вид:
.
График цифровой единичной функции
приведен на рис.9.
3.Экспонента.
Выражение для экспоненциальной функции имеет вид:
, где
- цифровая постоянная времени, которая
определяется при дискретизации
экспоненты.
Экспоненциальная функции имеет график, показанный на рис 10.
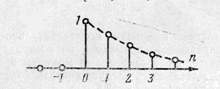
рис 10.
4.Синусоида.
Выражение для
цифровой синусоиды при переходе к
дискретному времени имеет вид
,
или в окончательно:
,
где
круговая
цифровая частота.
Введем циклическую
частоту дискретизации
,
тогда
,
где
циклическая цифровая частота.
Рассмотрим диапазоны изменения круговой и циклической цифровых частот.
При переходе
аналоговой синусоиды с частотой
в цифровую область, необходимо выбирать
минимальное значение частоты дискретизации
равным
.
При этом допустимые диапазоны изменения
цифровых частот определяся следующим
образом:
График цифровой синусоиды показан на рис.11.
рис.11.
СПОСОБЫ ОПИСАНИЯ ЦИФРОВЫХ ФИЛЬТРОВ
Z-преобразование
Операторный
метод,
базирующийся
на преобразовании Лапласа,
является
одним из основных направлений в
исследовании линейных
систем.
Преобразование Лапласа (.1) позволяет
осуществить перевод оригинала
из
области непрерывного времени t
в
его комплексное
изображение
E(s)
в
s-области.
,
(.1)
В
области дискретного времени преобразование
Лапласа последовательности
принимает
вид суммы:
(.2)
Трансцендентность
изображений дискретных .последовательностей
из-за наличия экспоненты в ( .2) приводит
к определенным
трудностям, поэтому применительно к
дискретным и цифровым устройствам
пользуются не дискретным
преобразованием Лапласа, а
-преобразованием,
которое
получается из (:2) заменой
:
(.3)
Свойства -преобразования.
Линейность. Если
и
являются
-преобразованиями
последовательностей
и
,
то любых действительных
а
и
b
z-преобразование
равно
Это
непосредственно вытекает из (.3)
и
является подтверждением принципа
суперпозиции из определения.
Задержка.
Если
-
преобразование относится
к
последовательности
,
то
-преобразование
последовательности
,задержанной
на
тактов,
равно
.
При определении
-преобразования
ординаты
в соответствии с
(.3)
умножаются на комплексные числа
последовательности
и
результаты
умножения
суммируются.
Очевидно,
что
-преобразование
будет точно таким
же, если оперировать несмещенной
последовательностью
и последовательностью
смещенной на т
тактов
в сторону опережения.
Формульная запись при этой операции имеет вид:
(.4)
Из (.4) следует, в частности, что в выражениях z-форм множитель z±m должен рассматриваться как оператор сдвига преобразуемой последовательности на т тактов дискретизации. Знак показателя определяет направление сдвига (минус - задержка, плюс - опережение).
Свертка.
Если
последовательности
соответствует
-преобразование
,
а
последовательности
-преобразование
,
то дискретной свертке этих
последовательностей:
(.5)
соответствует произведение их - преобразований:
(.6)
Обратное z-преобразование определяется формулой:
(.7)