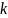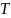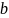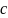2.1. Точные методы исследования нелинейных сау. Метод фазовой плоскости. 2. Анализ нелинейных систем автоматического управления.

Цель задания - исследование свободных режимов движения в нелинейной САУ методом фазовой плоскости.

Необходимо выполнить следующие задачи:

• Записать уравнения движения системы.

• Получить уравнения фазовых траекторий на фазовой плоскости 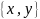, где .

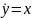• Коротко описать суть методов припасовывания и точечных преобразований.

• Определить асимптоты и линии переключения на фазовой плоскости.

• Определить параметры предельного цикла.

• Нарисовать фазовый портрет исследуемой нелинейной системы.

• Выбрать начальные условия внутри и вне предельного цикла и снять осциллограммы (по времени и на фазовой плоскости ).

№ варианта
1	0,5	0,1	0,01	0,8

Уравнения движения системы

T + T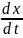 =−kF (x) , где F(x) принимает значения от –с до с.

F (x)= 0.8, x≥0.01, x’ ≥0

0.8, x≥−0.01, x’ <0

−0.8, x<0.01, x’ ≥0

−0.8, x<−0.01, x’ <0

Соответственно запишем уравнение движения так:

При 0.8, x≥0.01, x’ ≥0 или 0.8, x≥−0.01, x’ <0 : T + T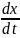 =−0,4

А при −0.8, x<0.01, x’ ≥0 или −0.8, x<−0.01, x’ <0 : T + T =0,4

Уравнение движения фазовых траекторий на фазовой плоскости {x,y}, где y=x’

Формулу уравнения движения T + T =−kF (x) можно представить в виде:

=y ; 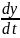= 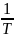(−kc−y);

На фазовой плоскости можно выделить две области, на которых F(x) принимает значения –с и с.

а) Для области 1, где F(x)= - c

=y ;

= 10 (−0,4−y);

=

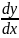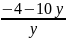
Решив это уравнение, получаем уравнение фазовых траекторий в области 1:

x=0.08 ln∣y+0.4∣−0 .1y+C1 .

б) для области 2, где F(x)=c

=y ;

= 10 (0,4−y);

=

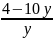
Решив это уравнение, получаем уравнение фазовых траекторий в области 2:

x=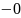 .08 ln∣y-0.4∣−0 .1y+C2 .

2.Метод точечных преобразований.

Метод точечного преобразования представляет собой усовершенствование метода

припасовывания с привлечением геометрических представлений в фазовом пространстве.

Запишем в общем виде уравнения динамики нелинейной системы второго порядка без

внешнего воздействия:

Н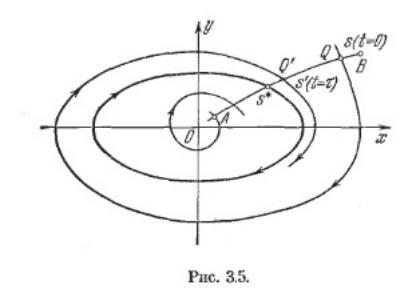 а фазовой плоскости (x, y) возьмем какой-нибудь отрезок линии АВ, который

пересекается фазовыми траекториями в одном направлении (рис. 3.5). Обозначим через s

координату произвольной точки Q на отрезке АВ, отсчитываемую вдоль дуги АВ от начала A

Пусть решение уравнений x = x(t), y = y(t)

дает фазовую траекторию, проходящую

через точку Q. Допустим далее, что с

увеличением t эта фазовая траектория

снова пересечет отрезок АВ в некоторой

другой точке Q' (рис. 3.5). Координату

точки Q' по дуге АВ обозначим s’. Точка Q' (первого следующего пересечения отрезка АВ той же фазовой траекторией) называется последующей по отношению к исходной точке Q. Зависимость s’ = f(s), соответствующая ходу фазовой траектории в силу решения уравнений (3.12), называется функцией последования. Функция последования определяет закон точечного преобразования для данной нелинейной системы.

Определение последующих точек по заданным исходным на отрезке АВ и называется

точечным преобразованием отрезка АВ самого в себя. Ввиду непрерывности

расположения фазовых траекторий исходные и последующие точки заполняют весь

отрезок. Однако каждая точка отрезка АВ не обязательно имеет последующую внутри

этого отрезка. Фазовые траектории, пересекающие отрезок, могут и не возвращаться к

нему.

Возможен такой случай, что последующая точка Q' совпадает с исходной Q, т. е. f(s) = s =

s*.

При этом мы получаем замкнутую фазовую траекторию (рис. 3.5): предельный цикл или

кривую, соответствующую особой точке типа ≪центр≫, и т. п. Последнее выясняется из

хода соседних фазовых траекторий. Случай (3.14) называется точечным преобразованием

точки Q самой в себя. Это неподвижная точка в общем точечном преобразовании отрезка

АВ.

Есть фазовая траектория, пересекающая отрезок АВ в точке Q. С увеличением времени t

э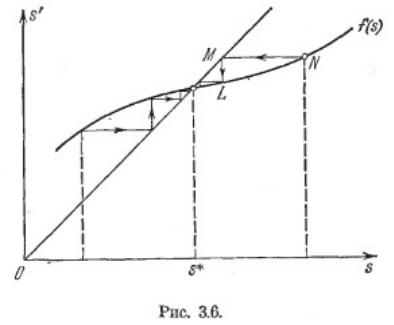 та траектория опять пересекает АВ в точке Q`. Координата точки Q по дуге АВ – s, точки Q` – s`. Точка Q- последующая к точке Q`. s`=f(s), соответствующая ходу фазовой траектории, называется функцией последования

(при f(s)=s=s* - замкнутая фазовая

траектория). Если процесс сходится к предельному циклу s*, то это устойчивый предельный цикл. Параметрическая форма: τ-параметр(содержащий время прохождения изображающей точки по фазовой траектории от исходной точки Q до её последующей Q`) Пусть в точке Q будет t = 0, а в точке Q1 обозначим t = τ. На участке фазовой траектории QQ1 имеем

F(x) = с. Поэтому уравнения принимают вид:

T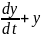 =−kc; =y;

Интегрирование их дает:

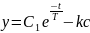
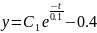
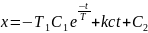
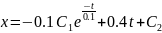
Обозначим ординаты точек Q и Q1 через y0 и y1 соответственно.

Закон точечного преобразования будем искать в виде функций y0  τ  , y1 τ  .

При начальных условиях (точка Q) t=0 , x=b , y=y0 определяются постоянные:

 ;

)  ;

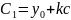
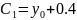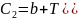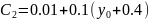Для Q1 t = τ, x = -b, y = y1:

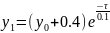-0.4

-0.02 = -0,1(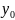 + 0.4)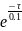 - 0.4τ + 0.02 + 0,02(y0+0.4)

Отсюда можно получить: y0(t) и у1(t).

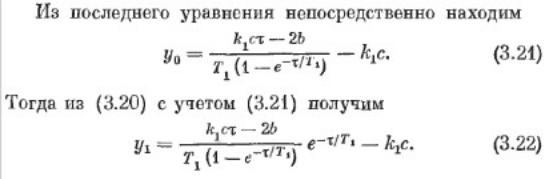
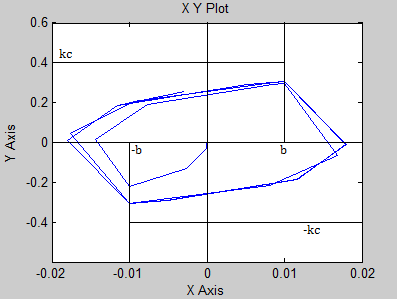
Определим асимптоты и линии переключения на фазовой плоскости:

Линии переключения: x = -0.02 и x = 0.02 (y = b и y = -b)

Асимптоты: y = -0.4 и y = 0.4 (y=-kc и y=kc)

Определим параметры предельного цикла:

Диаграмма точечного преобразования:

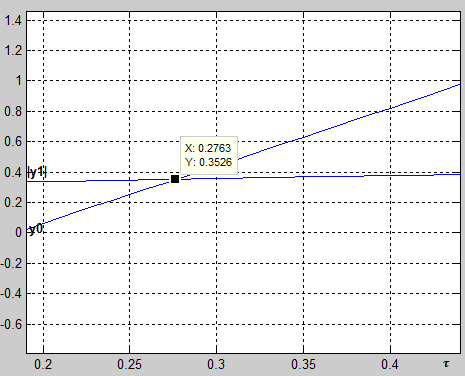
полупериод автоколебаний:

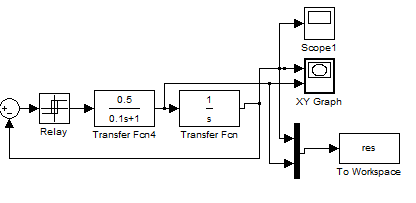
Нарисуем фазовый портрет искомой нелинейной системы. Схема нелинейной системы,

построена в simulink.

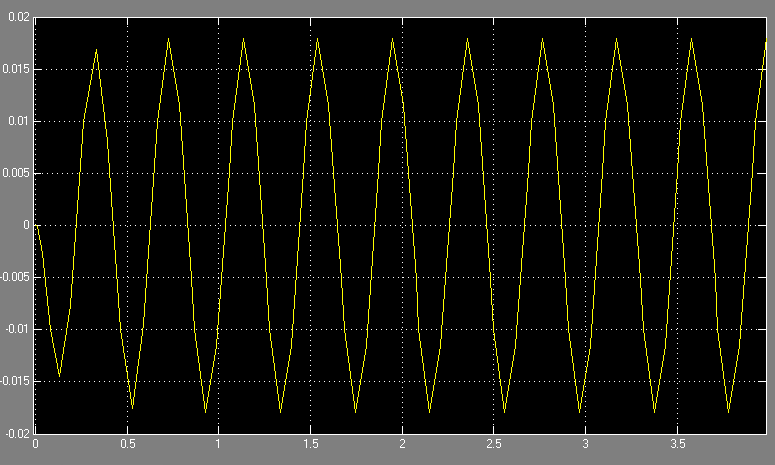
Осциллограммы (по времени и на фазовой плоскости), для начальных условий, внутри

предельного цикла.

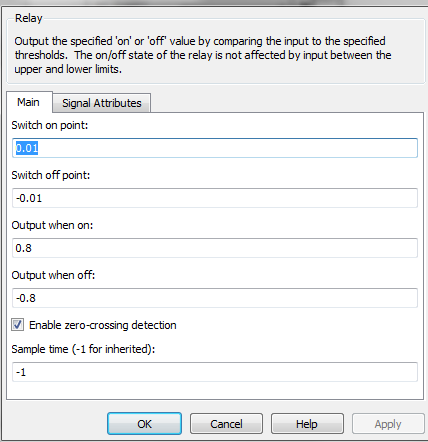
Настройки реле:

1. Switch on point - Порог включения. Значение, при котором происходит включение реле. (b)

2. Switch off point - Порог выключения. Значение, при котором происходит выключение реле. (-b)

3. Output when on - Величина выходного сигнала во включенном состоянии. (c)

4. Output when off - Величина выходного сигнала в выключенном состоянии. (-c)