
- •Тема 7. Теория графов
- •7.1. Основные понятия теория графов
- •7.2. Матричные способы задания графов
- •7.3. Изоморфизм графов
- •7.4. Маршруты и пути
- •7.5. Связность графа
- •7.6. Экстремальные пути в нагруженных ориентированных графах
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из в ( )
- •7.7. Эйлеровы и гамильтоновы графы
- •7.8. Деревья. Основные определения
- •7.9. Минимальные остовные деревья нагруженных графов
- •7.10. Задачи для самостоятельного решения
- •Литература
Тема 7. Теория графов
7.1. Основные понятия теория графов
Теория графов – это математический аппарат для формализации (моделирования) реальных задач по исследованию свойств конечных множеств с заданными отношениями между их элементами. В их числе задачи из области администрирования сетей, информационных потоков, планирования, проектирования и управления различными системами.
Первая работа по теории графов принадлежащая Эйлеру, появилась в 1736 году. Вначале эта теория была связана с математическими головоломками и играми. Однако впоследствии теория графов стала использоваться в топологии, алгебре, теории чисел. В наше время теория графов находит применение в самых разнообразных областях науки, техники и практической деятельности. Она используется при проектировании электрических сетей, планировании транспортных перевозок, построении молекулярных схем. Применяется теория графов также в информатике, экономике, психологии, социологии, биологии.
Задачи на графах удобно переводить на языки программирования, то есть решать с использованием современной вычислительной техники. Умение решать задачи на графах, в том числе и на персональных ЭВМ позволит будущему специалисту приобрести опыт разработки технологий и методов теории операций для решения задач при научных исследованиях и проектно-конструкторской деятельности.
Графы помогают описывать и исследовать различные системы объектов и их связи. Например, в графе, изображенном на рис. 13, точки (вершины графа) можно интерпретировать как города, а линии, соединяющие вершины (ребра), как дороги, соединяющие эти города.
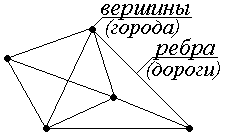
Рис. 13
Формальное
определение графа таково: Графом
![]() называется пара множеств:
называется пара множеств:
![]() – множество, элементы которого называются
вершинами,
– множество, элементы которого называются
вершинами,
![]() – множество неупорядоченных пар вершин,
называемых ребрами.
– множество неупорядоченных пар вершин,
называемых ребрами.
Для многих задач несущественно, являются ли ребра отрезками прямых или криволинейными дугами; важно лишь то, какие вершины соединяет каждое ребро.
Если ребрам графа
приданы направления от одной вершины
к другой, то такой граф называется
ориентированным,
т.е.
подмножество
![]() представляет собой упорядоченные пары.
Ребра ориентированного
графа называются дугами.
Соответствующие вершины ориентированного
графа называют началом
и концом.
Если направления ребер не указываются,
то граф называется неориентированным
(или просто графом). Неориентированное
ребро графа эквивалентно двум
противоположно направленным дугам,
соединяющим те же самые вершины. Множество
ребер графа может быть пустым. Множество
вершин графа не может быть пустым.
представляет собой упорядоченные пары.
Ребра ориентированного
графа называются дугами.
Соответствующие вершины ориентированного
графа называют началом
и концом.
Если направления ребер не указываются,
то граф называется неориентированным
(или просто графом). Неориентированное
ребро графа эквивалентно двум
противоположно направленным дугам,
соединяющим те же самые вершины. Множество
ребер графа может быть пустым. Множество
вершин графа не может быть пустым.
Граф, имеющий как ориентированные, так и неориентированные ребра, называется смешанным.
Пример. На
рис. 14 изображен неориентированный граф
.
![]() ,
,
![]() .
.
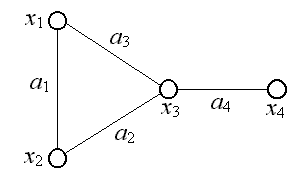
Рис. 14. Неориентированный граф
Пример. На
рис. 15. изображен ориентированный граф
.
,
![]() .
.
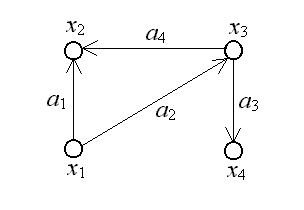
Рис. 15. Ориентированный граф
Пример. На
рис. 16. изображен ориентированный граф
.
,
![]() .
.

Рис. 16. Граф с пустым множеством дуг
Как в случае
ориентированного, так и в случае
неориентированного ребра говорят, что
вершины
![]() и
и
![]() инцидентны
ребру
инцидентны
ребру
![]() ,
если эти вершины соединены
.
Две вершины называются смежными,
если они инцидентны одному и тому же
ребру. Два ребра называются смежными,
если они имеют общую вершину. Степенью
вершины
графа
,
если эти вершины соединены
.
Две вершины называются смежными,
если они инцидентны одному и тому же
ребру. Два ребра называются смежными,
если они имеют общую вершину. Степенью
вершины
графа
![]() называется число ребер, инцидентных
этой вершине. Вершина, имеющая степень
0, называется изолированной,
а степень 1 – висячей.
Полустепенью
исхода (захода)
вершины
называется число ребер, инцидентных
этой вершине. Вершина, имеющая степень
0, называется изолированной,
а степень 1 – висячей.
Полустепенью
исхода (захода)
вершины
![]() ориентированного графа
ориентированного графа
![]() называется число
называется число
![]() (
(![]() )
дуг ориентированного графа
,
исходящих из
(заходящих в
).
)
дуг ориентированного графа
,
исходящих из
(заходящих в
).
Для ориентированного
графа множество вершин, в которые ведут
дуги, исходящие из вершины
,
обозначают
![]() ,
то есть
,
то есть
![]() .
Множество
называют образом
вершины
.
Соответственно
.
Множество
называют образом
вершины
.
Соответственно
![]() – множество вершин, из которых исходят
дуги, ведущие в вершину
,
то есть
– множество вершин, из которых исходят
дуги, ведущие в вершину
,
то есть
![]() .
Множество
называют
прообразом
вершины
.
.
Множество
называют
прообразом
вершины
.
Пример. В
графе, изображенном на рис. 14, концами
ребра
![]() являются
вершины
являются
вершины
![]() ;
вершина
;
вершина
![]() инцидентна
ребрам
инцидентна
ребрам
![]() ;
степень вершины
;
степень вершины
![]() равна
3;
вершины
равна
3;
вершины
![]() и
смежные;
ребра
и
и
смежные;
ребра
и
![]() смежные;
вершина
смежные;
вершина
![]() висячая. В
ориентированном графе, изображенном
на рис. 15, началом дуги
является
вершина
,
а ее концом
вершина x2;
вершина x1
инцидентна
дугам
и
;
висячая. В
ориентированном графе, изображенном
на рис. 15, началом дуги
является
вершина
,
а ее концом
вершина x2;
вершина x1
инцидентна
дугам
и
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если множеству
принадлежат пары
![]() ,
то такие ребра
,
то такие ребра
![]() называют петлями. Существование
одинаковых пар
называют петлями. Существование
одинаковых пар
![]() соответствует наличию параллельных
или кратных ребер (дуг), а кратностью
ребер называют количество таких
одинаковых пар.
соответствует наличию параллельных
или кратных ребер (дуг), а кратностью
ребер называют количество таких
одинаковых пар.
Например, кратность
ребра
![]() в графе, изображенном на рис. 17, равна
двум, кратность ребра
в графе, изображенном на рис. 17, равна
двум, кратность ребра
![]() равна трем.
равна трем.
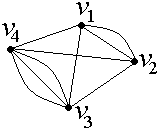
Рис. 17. Граф с кратными ребрами
Граф, содержащий
кратные ребра, называется мультиграфом.
Граф с кратными ребрами и петлями
называется
псевдографом.
Следует
заметить, что в случае ориентированного
псевдографа вклад каждой петли инцидентной
вершине
равен 1 как в
![]() ,
так и в
,
так и в
![]() .
.
Подграфом
неориентированного
графа
называется
граф, все вершины и ребра которого
содержатся среди вершин и ребер графа
.
Аналогично определяется подграф
ориентированного графа. Подграф
называется собственным,
если он отличен от самого графа. Граф
– полный,
если для любой пары вершин
![]() и
и
![]() существует
ребро
существует
ребро
![]() .
Граф
– симметрический,
если для любой дуги
существует противоположно ориентированная
дуга
.
Граф
– симметрический,
если для любой дуги
существует противоположно ориентированная
дуга
![]() .
Граф
– планарный,
если он может быть изображен на плоскости
так, что не будет пересекающихся дуг.
Неориентированный граф
– двудольный,
если множество его вершин
.
Граф
– планарный,
если он может быть изображен на плоскости
так, что не будет пересекающихся дуг.
Неориентированный граф
– двудольный,
если множество его вершин
![]() можно разбить
на два такие подмножества
можно разбить
на два такие подмножества
![]() и
и
![]() ,
что каждое ребро имеет один конец в
,
а другой в
.
,
что каждое ребро имеет один конец в
,
а другой в
.
