
Дифференциальные уравнения.
Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких – то уравнением в частных производных.
Дифференциальное
уравнение можно записать в виде:
![]() ,
где
,
где![]() – некоторая функция
– некоторая функция![]() переменных
переменных![]() .
.
Порядок
![]() старшей производной называетсяпорядком
дифференциального уравнения.
старшей производной называетсяпорядком
дифференциального уравнения.
Дифференциальное
уравнение
![]() -го
порядка называетсяразрешенным
относительно старшей производной, если
оно имеет вид:
-го
порядка называетсяразрешенным
относительно старшей производной, если
оно имеет вид:
![]() ,
где
,
где![]()
некоторая функция от
некоторая функция от
![]() переменной.
переменной.
Решением
дифференциального уравнения
![]() называется функция
называется функция![]() ,
которая при подстановке ее в это уравнение
обращает его в тождество.
,
которая при подстановке ее в это уравнение
обращает его в тождество.
Пример.
Найти решение дифференциального
уравнения
![]() .
.
Решение:
![]()
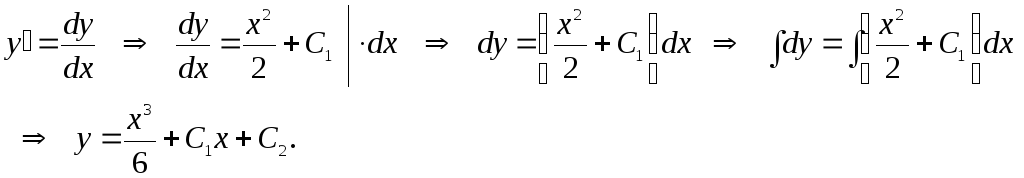
Ответ:
![]()
Общим
решением дифференциального уравнения
![]()
![]() -го
порядка называется такое его решение
-го
порядка называется такое его решение![]() ,
которое является функцией переменной
,
которое является функцией переменной![]() и
и![]() произвольных постоянных
произвольных постоянных![]() .
.
Частным
решением дифференциального уравнения
![]() называется решение, получаемое из общего
решения при некоторых конкретных
числовых значениях
называется решение, получаемое из общего
решения при некоторых конкретных
числовых значениях![]() .
.
Пример.
Рассмотрим дифференциальное уравнение
из предыдущего примера
![]() .
Тогда общим решением будет
.
Тогда общим решением будет
![]() ,
,
а
частным решением:
![]() или
или![]() .
.
Дифференциальные уравнения первого порядка.
Дифференциальное
уравнение первого порядка
имеет вид:
![]() или
или![]() ,
где
,
где![]() – независимая переменная;
– независимая переменная;![]()
неизвестная функция и ее производная.
неизвестная функция и ее производная.
Учитывая,
что
![]() уравнение первого порядка можно записать
в форме:
уравнение первого порядка можно записать
в форме:![]() .
.
Общим
решением
дифференциального уравнения первого
порядка называется функция вида
![]() ,
где
,
где![]() – произвольная постоянная, удовлетворяющая
условиям:
– произвольная постоянная, удовлетворяющая
условиям:
Для любого значения
 она является решением уравнения;
она является решением уравнения;При любом допустимом начальном условии
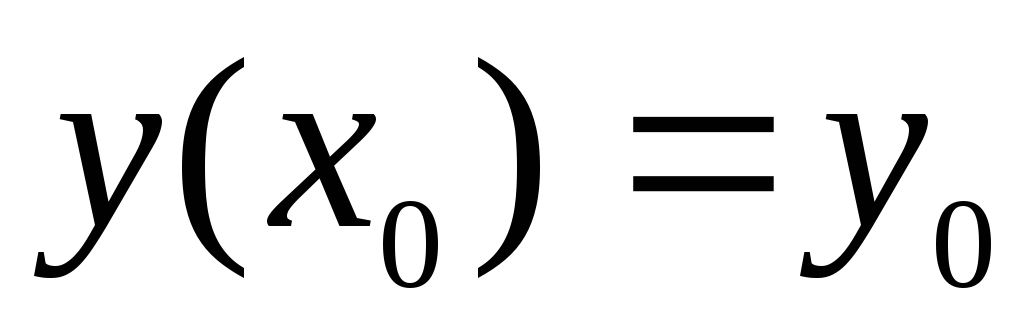 найдется такое значение
найдется такое значение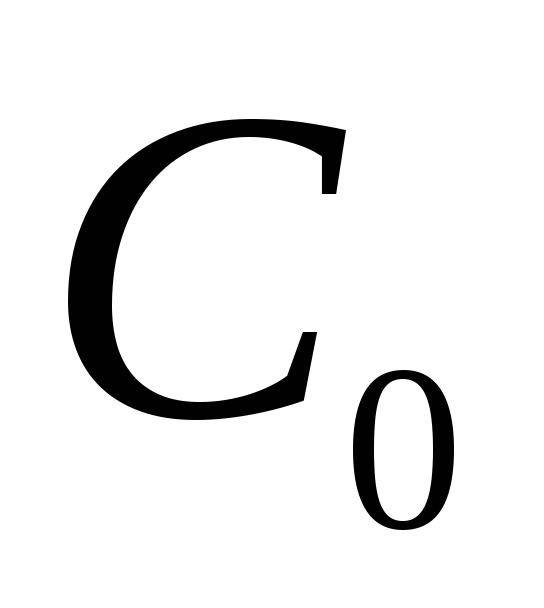 ,
что
,
что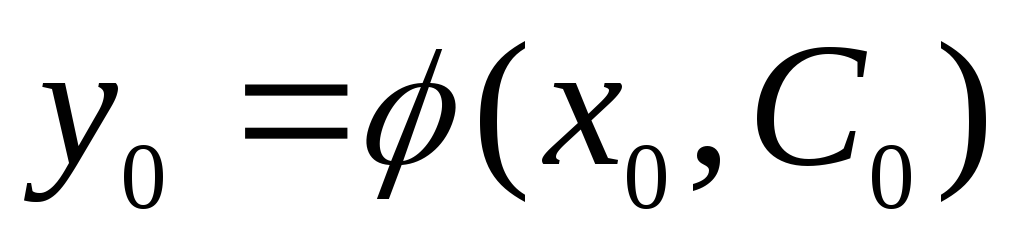 .
.
Если общее решение не представлено в явном виде, то оно называется общим интегралом.
Задача
нахождения частного решения,
удовлетворяющего заданному начальному
условию
![]() ,
называетсязадачей
Коши.
,
называетсязадачей
Коши.
Пример.
Дана задача Коши
![]() .
Найти частное решение.
.
Найти частное решение.
Решение: Общее решение имеет вид
![]() ,
,
![]() .
.
Подставляем начальные условия:
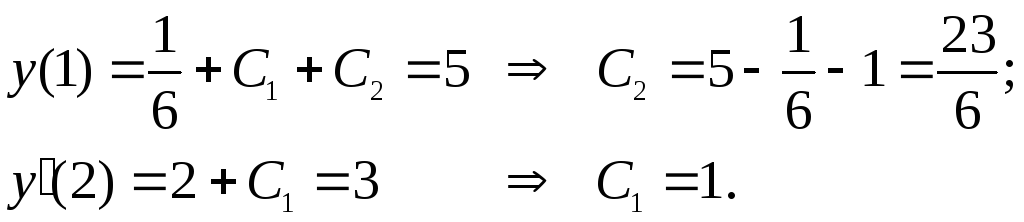
Получим,
что частное решение данной задачи Коши
![]() .
.
Ответ:
![]() .
.
Теорема
Коши о существовании и единственности
решения.
Пусть дано дифференциальное уравнение
![]() .
Если функция
.
Если функция![]() и ее частная производная
и ее частная производная![]() непрерывны в некоторой области
непрерывны в некоторой области![]() плоскости
плоскости![]() ,
то в некоторой окрестности любой
внутренней точки
,
то в некоторой окрестности любой
внутренней точки![]() этой области существует единственное
решение уравнения
этой области существует единственное
решение уравнения![]() ,
удовлетворяющее условию
,
удовлетворяющее условию![]() при
при![]() .
.
Геометрически
общее решение представляет собой
однопараметрическое семейство
интегральных кривых на плоскости
![]() .
Частное решение – одна из кривых этого
семейства, проходящая через точку
.
Частное решение – одна из кривых этого
семейства, проходящая через точку![]() .
.
Типы дифференциальных уравнений первого порядка:
Дифференциальное уравнение с разделяющимися переменными имеет вид:
![]() или
или
![]() ,
,
где
![]() – непрерывные функции.
– непрерывные функции.
Разделив
обе части уравнения на
![]() ,
получим уравнение:
,
получим уравнение:
![]() ,
,
![]() .
.
В
полученных уравнениях левая часть
зависит только от
![]() ,
а правая часть только от
,
а правая часть только от![]() ,
т.е. переменные разделены.
,
т.е. переменные разделены.
Поскольку
дифференциалы равны, то их неопределенные
интегралы различаются на постоянную
величину. Интегрируя слева по переменной
![]() ,
а справа по переменной
,
а справа по переменной![]() ,
получаем:
,
получаем:
![]() или
или
![]() .
.
Пример.
Найти частное решение дифференциального
уравнения
![]() при начальных условиях
при начальных условиях![]() .
.
Решение:

![]() .
.
Ответ:
![]() .
.
Пример.
Найти решение дифференциального
уравнения
![]() .
.
Решение:

Ответ:
![]() .
.
Неполные дифференциальные уравнения первого порядка
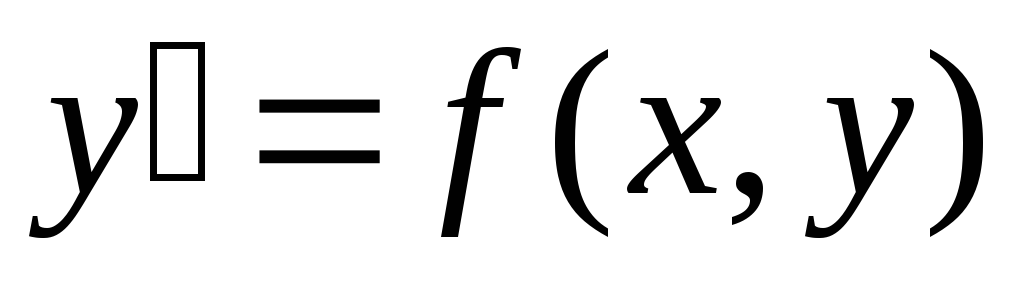 – это дифференциальные уравнения, в
которых функция
– это дифференциальные уравнения, в
которых функция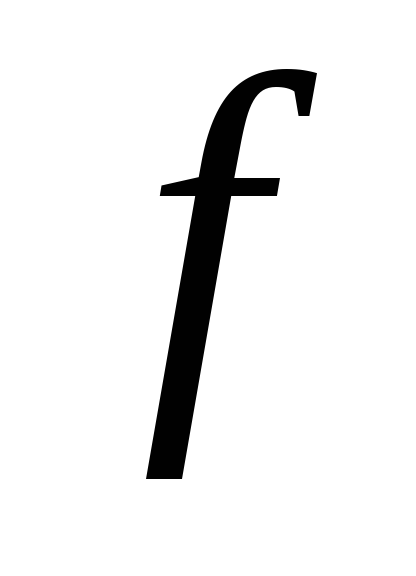 явно зависит только от одной переменной:
явно зависит только от одной переменной:
А)
Пусть
![]() зависит только от
зависит только от![]() ,
тогда
,
тогда![]() ,
откуда получаем:
,
откуда получаем:![]() .
.
Б)
Пусть
![]() зависит только от
зависит только от![]() ,
т.е.
,
т.е.![]() – это уравнение называетсяавтономным.
Откуда получаем:
– это уравнение называетсяавтономным.
Откуда получаем:
![]() .
.
Линейные дифференциальные уравнения первого порядка имеют вид:
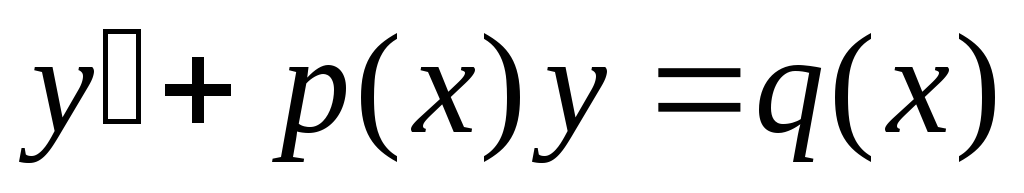 .
.
Если
![]() ,
то уравнение
,
то уравнение![]() называетсялинейным
однородным уравнением,
если
называетсялинейным
однородным уравнением,
если
![]() ,
то –линейным
неоднородным уравнением.
,
то –линейным
неоднородным уравнением.
А)
Однородное
уравнение
– это уравнение, приводящееся к виду:
![]() .
Подстановкой
.
Подстановкой![]() однородное уравнение сводится к уравнению
с разделяющимися переменными.
однородное уравнение сводится к уравнению
с разделяющимися переменными.
Пример.
Найти решение дифференциального
уравнения
![]() .
.
Решение: Воспользуемся подстановкой, приводящей исходное уравнение к уравнению с разделяющимися переменными, и решим его:
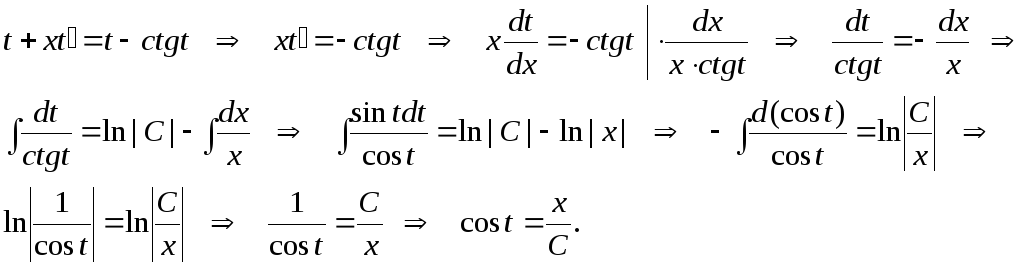 Выполним
обратную замену и получим искомое
решение:
Выполним
обратную замену и получим искомое
решение:
![]()
Ответ:
![]() .
.
Б)
Линейное
неоднородное дифференциальное уравнение
![]() подстановкой
подстановкой![]() сводится
к уравнению
сводится
к уравнению![]() .
Далее требуется, чтобы
.
Далее требуется, чтобы![]() ,
тогда из этого уравнения можно найти
,
тогда из этого уравнения можно найти![]() ,
а из предыдущего зная
,
а из предыдущего зная![]() ,
находят
,
находят![]() .
Зная
.
Зная![]() и
и![]() ,
находят
,
находят![]() .
.
Для
решения неоднородного линейного
уравнения также можно использовать
метод
вариации произвольных постоянных.
Этот метод состоит в том, что сначала
находят общее решение соответствующего
однородного линейного уравнения, т.е.
![]() .
Затем, полагают в решении однородного
уравнения
.
Затем, полагают в решении однородного
уравнения![]() величину
величину![]() ищут решение неоднородного уравнения.
Для этого подставляют в неоднородное
уравнение
ищут решение неоднородного уравнения.
Для этого подставляют в неоднородное
уравнение![]() и
и![]() ,
и из полученного дифференциального
уравнения определяют функцию
,
и из полученного дифференциального
уравнения определяют функцию![]() .
Таким образом, общее решение неоднородного
уравнения имеет вид:
.
Таким образом, общее решение неоднородного
уравнения имеет вид:![]() .
.
Пример. Найти решение дифференциального уравнения
![]() .
.
Решение: 1 способ.
Используя
подстановку
![]() ,
уравнение примет вид
,
уравнение примет вид
![]()
Приравнивая
скобку к нулю, находим
![]() :
:
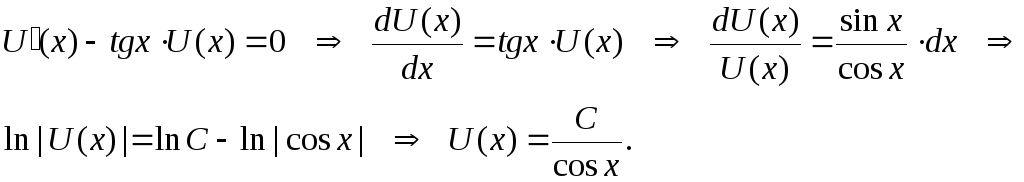
Зная
![]() ,
можно посчитать
,
можно посчитать![]() :
:
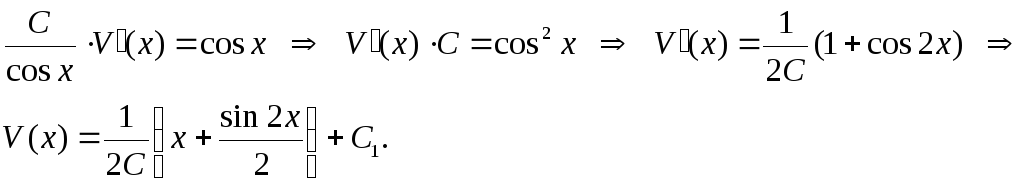
Ответ:
![]() .
.
2способ. Находим общее решение соответствующего однородного линейного уравнения
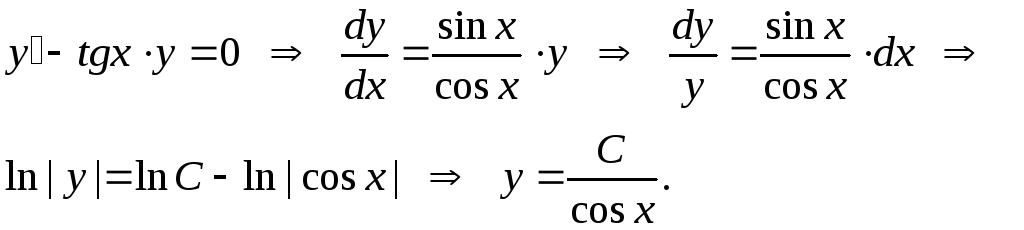
Пусть
в решении однородного уравнения величина
![]() ,
получим решение неоднородного уравнения
,
получим решение неоднородного уравнения
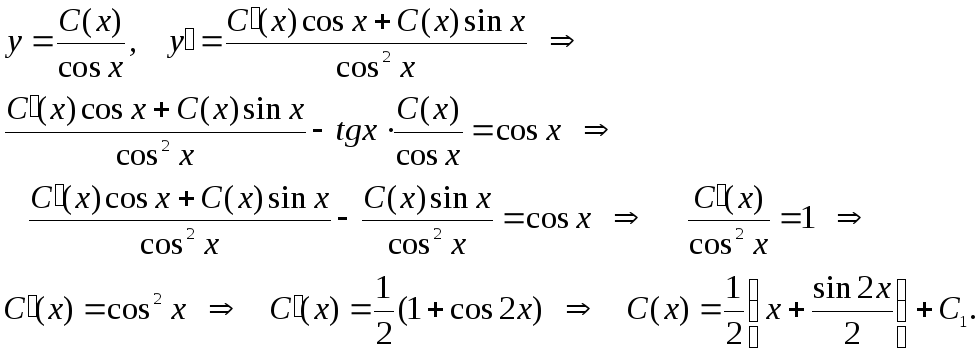
Ответ:
![]() .
.
Уравнение Бернулли – это нелинейное уравнение, которое можно привести к линейному соответствующей заменой неизвестной функции
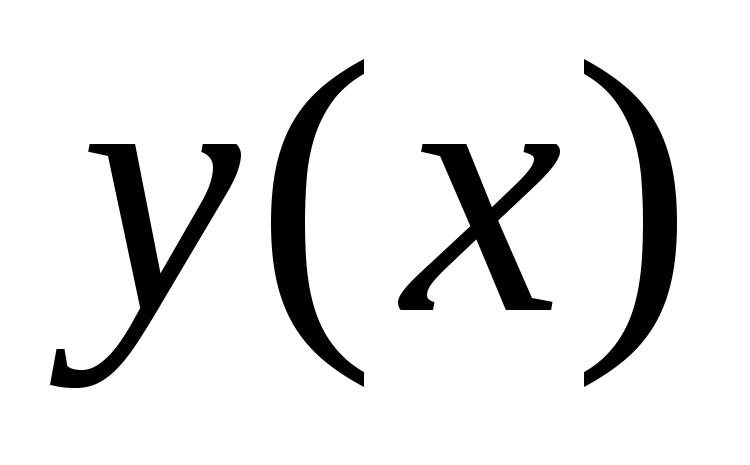 .
Уравнение Бернулли имеет вид:
.
Уравнение Бернулли имеет вид: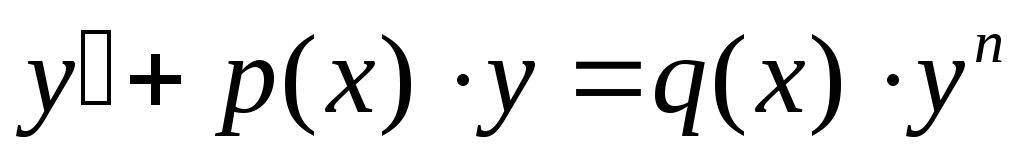 ,
где
,
где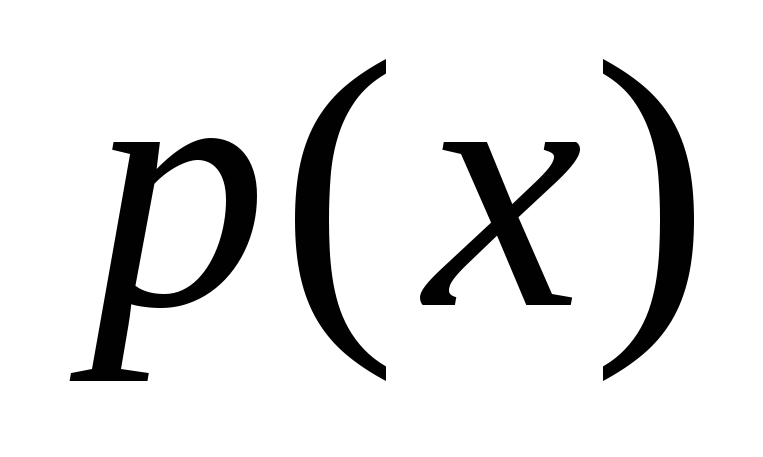 и
и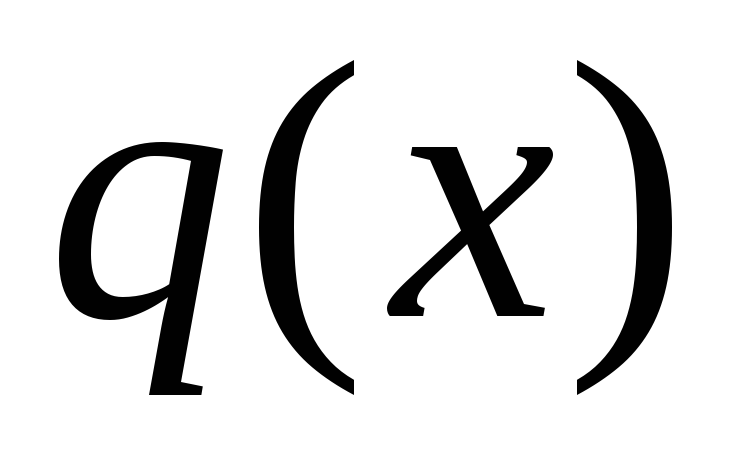 – непрерывные функции;
– непрерывные функции;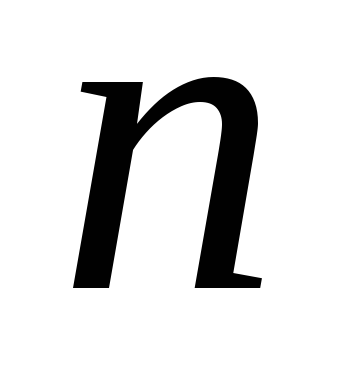
постоянное число,
постоянное число,
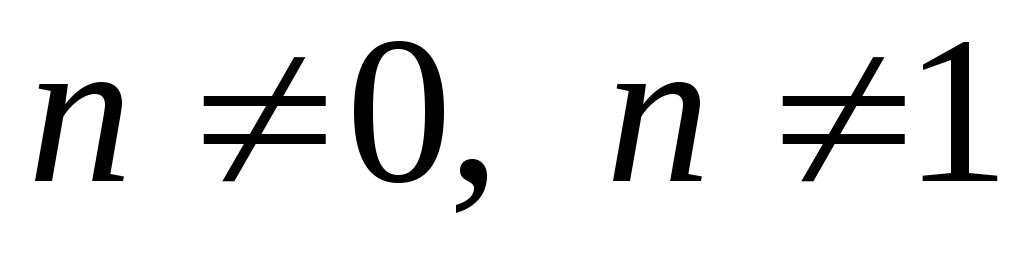 .
Данное уравнение приводится к линейному
заменой
.
Данное уравнение приводится к линейному
заменой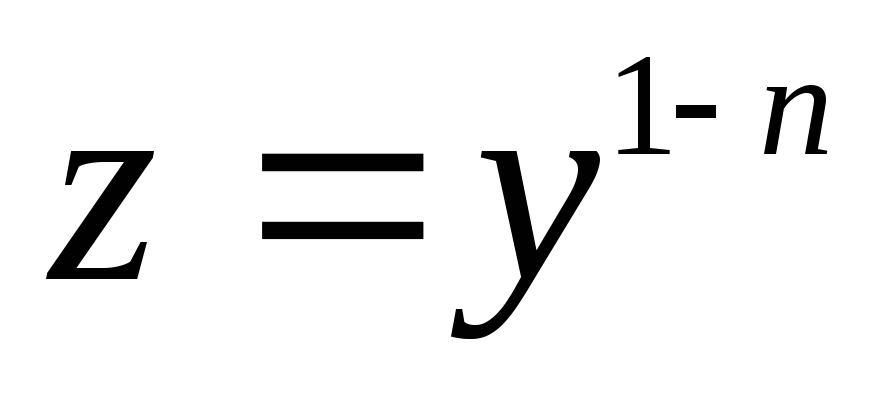 тогда
тогда .
Разделим обе части уравнения Бернулли
на
.
Разделим обе части уравнения Бернулли
на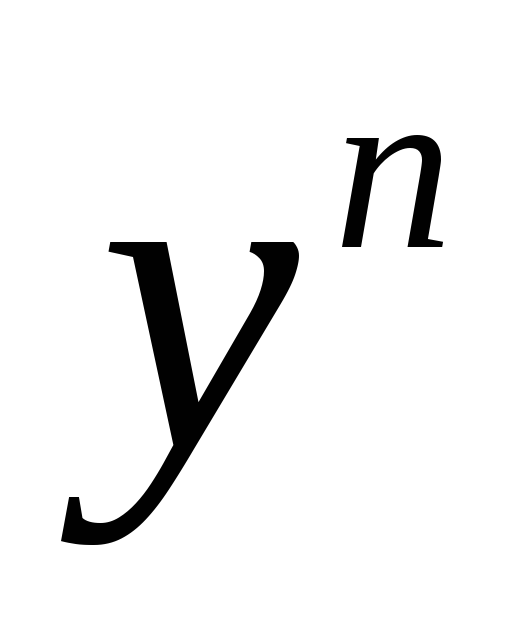 :
: .
Умножим обе части на
.
Умножим обе части на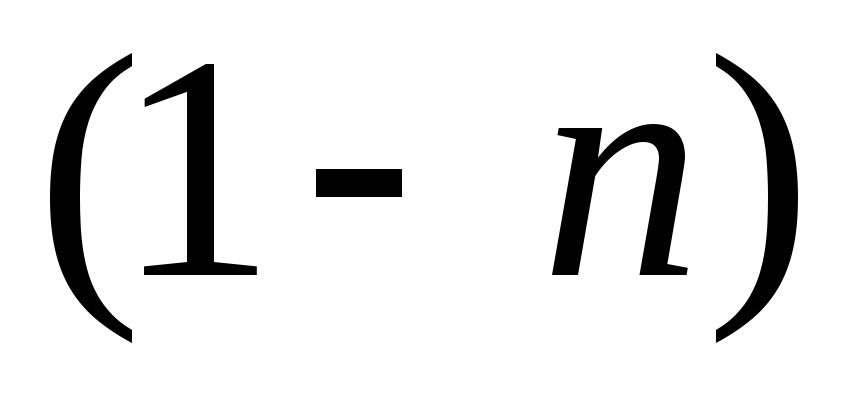 :
: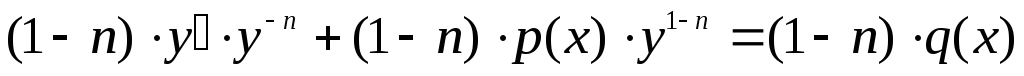 .
Переходим к
.
Переходим к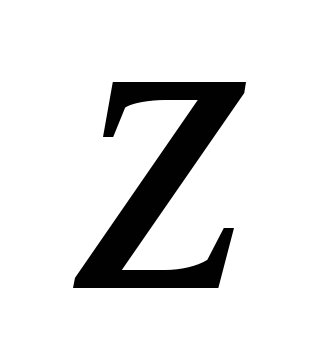 :
: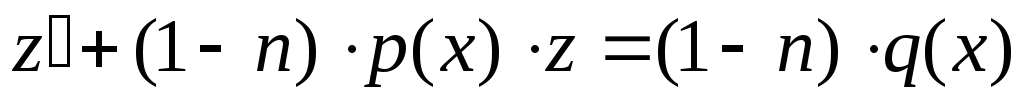 .
.
Пример.
Найти решение дифференциального
уравнения
![]() .
.
Решение:
Разделим обе части уравнения на
![]() и умножим на
и умножим на![]() ,
получим
,
получим![]() .
Используя замену
.
Используя замену![]() ,
наше уравнение примет вид
,
наше уравнение примет вид![]() ,
а это линейное неоднородное дифференциальное
уравнение.
,
а это линейное неоднородное дифференциальное
уравнение.
Найдем
сначала решение однородного уравнения:
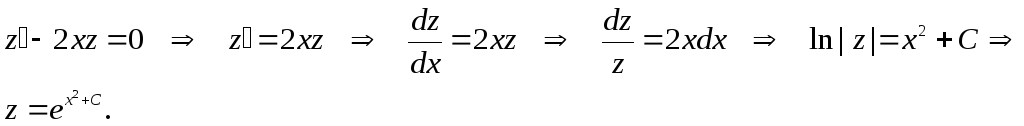
Принимаем
![]() и находим решение неоднородного
уравнения:
и находим решение неоднородного
уравнения:

Ответ:
![]() .
.
