Работа № 4 Решение краевой задачи методом стрельбы

Рассмотрим краевую задачу для линейного ДУ 2-го порядка:

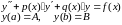(3)

Общее решение уравнения (1) имеет вид

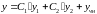, (4)

где и 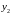– линейно независимые частные решения однородного уравнения;

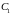и 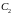– произвольные постоянные;

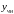– некоторое частное решение неоднородного уравнения.

При подстановке в (4) краевых условий 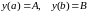получим систему уравнений относительно и :

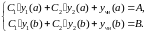(5)

Допустим, что известно частное решение уравнения (3), удовлетворяющее условию

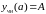, (6)

обыкновенных дифференциальных уравнений (ОДУ) а также одно из частных решений соответствующего уравнения, отвечающего условию

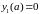(7)

Тогда первое уравнение системы (3) примет вид

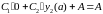
И следовательно, 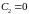. Постоянную определяем из уравнения

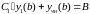. (8)

Метод, при котором предварительно отыскивают численные решения и , удовлетворяющие (6) и (7), а затем находят 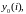исходя из (8), называют методом стрельбы.

Для численного решения задачи разобьем отрезок на равных частей точками

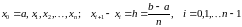
И обозначим

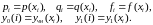
Будем искать численные решения 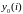и исходя из условий:

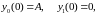(9)

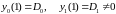(10)

(для уменьшения вычислительной погрешности обычно берут и )

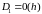Для численного решения данного уравнения используем разностную аппроксимацию производных. Для этого выразим и 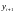по формуле Тейлора

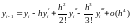, (11)

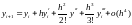, (12)

Из формул (11) и (12) легко получить

,

Для определения 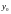и получим систему из уравнений:

(13)

Отсюда, используя (7) и (8), получим

(14)

В результате последовательно определяем все ординаты . Теперь для определения используем (8): 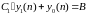, откуда

Окончательно искомое численное решение краевой задачи (3) в точках разбиения получим по формулам

.

Составим программу в пакете MathCad, реализующую метод стрельбы.

Рассмотрим в качестве примера ДУ второго порядка из лабораторной работы №2: .

Решение ищем на отрезке [1,2]. Значение константы 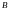найдем из аналитического решения этого уравнения (см. работу №2) : . Подставим в него 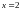, тогда .

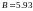Разделим исходное уравнение на коэффициент, стоящий перед второй производной ( в нашем примере 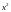) и получим:

.

Преобразуем его к виду (1) .

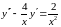Здесь

Программу составим в общем виде для уравнения вида (1).

Результат вычислений сохраняется в матрице С, у которой первый столбец – переменная x, второй ­– значен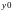ия , а третий – значения .

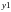Для проверки найденного решения вывести значения функции, полученные из его аналитического решения.

В MathCad для решения краевой задачи можно использовать функции sbval и bvalfit. Эти функции можно использовать для системы ОДУ, решение которых является функцией одной переменной, и известны значения решения в двух граничных точках интервала.

Рассмотрим, как можно использовать эти функции. Пусть у нас есть ДУ n-го порядка и известны не все начальные условия в начальной точке интервала, но известны дополнительно значения решения и/или некоторых его производных в другой точке интервала. Общее количество условий, заданных в граничных точках интервала равно n.

Для того чтобы найти недостающие начальные условия в точке 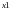, надо использовать функцию sbval. После того как эти недостающие начальные условия будут получены, можно решать обычную задачу Коши, используя для ее решения ранее рассмотренные функции.

ФУНКЦИИ ИЗ МАТКАДА

Задание

1. Решить аналитически задачу Коши и найти значение решения в точке 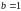. Краевое условие .

2. Решить задачу методом стрельбы.

3. Вычислить точное решение 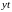с тем же шагом и величину .

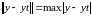Варианты задания взять в работе № 3.

Отчет оформить как файл пакета MathCad. Отчет должен содержать постановку задачи и метод решения, точное решение уравнения, таблицу значений точного и приближенного решений в заданных точках..

Варианты работы № 4

Значения и во всех вариантах равны 0 и 1, соответственно . Варианты взять из работы № 1.