
- •Определение объединения множеств. Свойства операции объединения множеств.
- •Определение пересечения множеств. Свойства операции пересечения множеств.
- •Определение разности множеств. Свойства операции нахождения разности множеств.
- •Свойства
- •Определение симметрическая разность множеств. Свойства операции нахождениясимметрической разности множеств.
- •Свойства
Вопросы по дискретной математике
Определение объединения множеств. Свойства операции объединения множеств.
Множество,
содержащее в себе все элементы исходных
множеств. Объединение двух
множеств ![]() и
и ![]() обычно
обозначается
обычно
обозначается ![]() ,
но иногда можно встретить запись в виде
суммы
,
но иногда можно встретить запись в виде
суммы ![]()
Объединение множеств является бинарной операцией на произвольном булеане
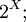
Операция объединения множеств коммутативна:
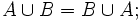
Операция объединения множеств ассоциативна:
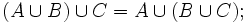
Операция объединения множеств дистрибутивна относительно операции пересечения:[1]
![]()
Пустое множество
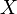 является нейтральным
элементом операции объединения
множеств:
является нейтральным
элементом операции объединения
множеств:
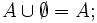
Таким образом булеан вместе с операцией объединения множеств является моноидом;
Операция объединения множеств идемпотентна:
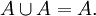
Определение пересечения множеств. Свойства операции пересечения множеств.
Пересече́ние мно́жеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.
Свойства
Пересечение множеств является бинарной операцией на произвольном булеане
 ;
;Операция пересечения множеств коммутативна:
![]()
Операция пересечения множеств ассоциативна:
![]()
Операция пересечения множеств дистрибутивна относительно операции объединения:[1]
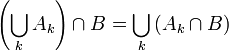
Универсальное множество
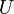 является нейтральным
элементом операции пересечения
множеств:
является нейтральным
элементом операции пересечения
множеств:
![]()
Таким образом булеан вместе с операцией пересечения множеств является абелевой группой;
Операция пересечения множеств идемпотентна:
![]()
Если
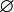 — пустое
множество, то
— пустое
множество, то
![]()
Определение разности множеств. Свойства операции нахождения разности множеств.
Разность двух множеств — это теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество
Свойства
Пусть ![]() —
произвольные множества.
—
произвольные множества.
Вычитание множества из самого себя даёт в результате пустое множество:
![]()
Свойства пустого множества относительно разности:
![]()
![]()
Разность двух множеств содержится в уменьшаемом:
![]()
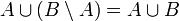 .
Из этой формулы следует, что операция
разности не является обратной операции
суммы (то есть объединению).
.
Из этой формулы следует, что операция
разности не является обратной операции
суммы (то есть объединению).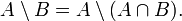
Разность не пересекается с вычитаемым:
![]()
Разность множеств равна пустому множеству тогда, и только тогда, когда уменьшаемое содержится в вычитаемом:
![]()
Законы де Моргана в алгебре множеств формулируются следующим образом:
![]()
![]()
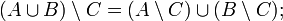
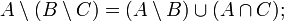
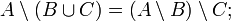

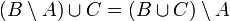 ,
если
,
если 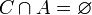 .
.Если
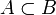 и
и 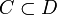 ,
то
,
то 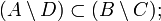
Если , то для любого
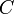 выполняется
выполняется 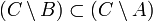 .
Это соотношение имеет свой аналог
в арифметике:
если
.
Это соотношение имеет свой аналог
в арифметике:
если  ,
то для любого
,
то для любого  справедливо
справедливо 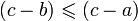 .
.
Определение симметрическая разность множеств. Свойства операции нахождениясимметрической разности множеств.
Симметрическая разность двух множеств — это теоретико-множественная операция, результатом которой является множество элементов этих множеств, принадлежащих только одному из них.
Свойства
Симметрическая разница является бинарной операцией на любом булеане;
Симметрическая разность коммутативна:
![]()
Симметрическая разность ассоциативна:
![]()
Пересечение множеств дистрибутивно относительно симметрической разности:
![]()
Пустое множество является нейтральным элементом симметрической разности:
![]()
Любое множество обратно само себе относительно операции симметрической разности:
![]()
В частности, булеан с операцией симметрической разности является абелевой группой;
Булеан с операцией симметрической разности также является векторным пространством над полем
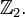
В частности, булеан с операциями пересечения множеств и симметрической разности является алгеброй с единицей.
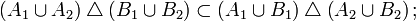
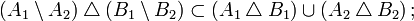
Если роль «суммы» играет операция симметрической разности, а роль «произведения» — пересечение множеств, то множества образуют кольцо без единицы. Причём другие основные операции теории множеств, разность и объединение, можно выразить через них:
![]()
![]()
В чем заключается метод двух включений доказательства теоретикомножественных тождеств?
Чтобы доказать равенство двух множеств Х и Y, т.е что X=Y, достаточно доказать два включения XY и YC-X, т.е доказать, что из предположения X∈Y( для произвольного x) следует, что X∈y, и , наоборот , из предположения Xey следует, что X∈x
Основные тождества для объединения, пересечения, дополнения множеств.
Основные тождества для пересечения и симметрической разности множеств.
Что называют характеристической функцией множества?
Характеристической
функцией множества ХС_U
называется функция, определенная
следующим образом
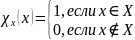
В чем заключается метод характеристических функций доказательства теоретико-
множественных тождеств?
Метод характеристических функций доказательства спра-
ведливости теоретико-множественного тождества заключается
в выражении характеристических функций обеих его частей
через характеристические функции входящих в него множеств.
Тождество верно тогда и только тогда, когда характеристиче-
ские функции левой и правой частей совпадают.
Что называют декартовым произведением множеств? Свойства декартова произве-
дения множеств.
Декартово
произведение ![]() множества
и
множества
множества
и
множества ![]() есть
такое множество
,
элементами которого являются упорядоченные
пары
есть
такое множество
,
элементами которого являются упорядоченные
пары ![]() для
всевозможных
для
всевозможных ![]() и
и ![]()
.
Что называют отображением из множества А в множество В?
Отображением множества А в множество В называют правило (соответствие), которое каждому элементу множества А ставит в соответствие единственный для этого элемента элемент множества В.
Что такое композиция отображений?
Пусть f – отображение множества A в множество B, g – отображение множества Bв множество C. Композицией отображений f и g называется отображение
h = gof, которое сопоставляет любому элементу a множества A элемент h(a)= g(f(a))
Что такое обратимое отображение?
Отображение f называется обратимым, если при этом отображении различные элементы множества X переходят в различные элементы множества Y.
Что такое обратное отображение?
Пусть F: X → Y. Если существует такое отображение Φ: Y → X, что ΦF = eX, FΦ = eY, то отображение Φ называют обратным к отображению F. В этом случае F называют обратимым отображением
Что называют бинарным отношением на множестве?
Бинарным
отношением в
множестве E называется
всякое подмножество B из
произведения
![]() .
.
Бинарное
отношение ![]() называется отношением
эквивалентности в
множестве E,
если подмножество
:
a)
рефлексивно:
называется отношением
эквивалентности в
множестве E,
если подмножество
:
a)
рефлексивно: ![]()
![]()
![]() ;
б)
симметрично:
;
б)
симметрично: ![]()
![]()
![]() ;
в)
транзитивно:
;
в)
транзитивно: ![]()
![]()
![]()
![]() .
.
Вместо ![]() часто
пишут a ~ b или a = b.
часто
пишут a ~ b или a = b.
Что называют n-арным отношением на множествах?
Произвольное подмножество (ро) декартова произведения А1х…хАn называют n-арным отношением на множествах A1,…,An В случае если все множества A1,…,An совпадают, т.е A1=…=An=A, говорят об n-арном отношении на множестве A.
Что называют классом эквивалентности?
Пусть р — эквивалентность на множестве А и х Е А. Мно-
жество всех элементов А, эквивалентных х, т.е. множество
{у: у ро x}, называют классом эквивалентности по отноше-
нию р и обозначают [х]р.
Что называют разбиением множества?
Пусть
А — произвольное множество. Семейство
непустых и попарно не пересекающихся
множеств называют разбиением множества
А, если объединение множеств семейства
(Bi)i∊I
равно А, т.е.
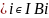 = А.
= А.
Какой порядок на множестве называют линейным?
Упорядоченное множество, все элементы которого попарно
сравнимы, называют линейно упорядоченным, а соответ-
ствующее отношение — отношением линейного порядка
(или просто линейным порядком).
Что такое счетное множество?
Любое множество, равномощное множеству всех натураль-
ных чисел, называют счетным. Мощность счетного множества
обозначают No (читается „алеф нуль").
Является ли счетным множество целых, рациональных, вещественных чисел. Ответ
обосновать.
Думаю нет, т.к счетные только положительные целые числа. Вышестоящие варианты к ним не относятся.
Дать определение булевой переменной, булевой функции, существенной и фиктив-
ной переменной. Равенство булевых функций
Булева функция (от п переменных) — это произвольное
отображение вида f:{0,1}^n {0,1}, т.е. булева функция определена на множестве всех п-элементных (при п ^ 0) последовательностей (или п-компонентных кортежей) нулей и единиц и принимает два возможных значения: 0 и 1.
Булево
переменное — это индивидное переменное
с областью значений {0,1}, т.е. это переменное,
которое может принимать только два
значения: 0 и 1 (подобно тому, как
действительное переменное принимает
произвольное действительное значение,
а комплексное переменное — произвольное
комплексное значение). Тогда с
использованием понятия булева переменного
мы можем задать булеву функцию f:{0,1}^n
{0,1},) записью у = f(x1,...
,xn),
в которой каждое булево переменное xi,i
=
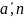 ,
,
и функция f принимают два возможных значения: 0 и 1. Пере-
менные xi, ..., хn называют при этом переменными булевой
функции f.
Описать способы задания булевой функции: табличный, векторный, с помощью
формулы, картой Карно. Привести пример функции, заданной векторным способом.
Долго писать, проще устно
Дать определение булевой функции сохраняющей константу 0 и константу 1. При-
вести пример.
Булева функция называется сохраняющей константу ноль , если на нулевом наборе аргументов она принимает значение равное нулю, то есть f(0,0,0,...,0) = 0;
f(x1,x2)= x1 v x2
Булева функция называется сохраняющей константу единица , если на единичном наборе аргументов она принимает значение равное единице, то есть f(1,1,1,...,1)= 1;
f(x1,x2)= x1 v x2
Дать определение линейной булевой функции. Привести примеры линейной и не-
линейной функции.
Булева
функция ![]() называется
линейной, если существуют такие
называется
линейной, если существуют такие ![]() ,
где
,
где ![]() ,
что для любых
,
что для любых ![]() имеет
место равенство:
имеет
место равенство:
![]() .
.
xy(x + y) – нелинейная, f=1 – нелинейная
Дать определение монотонной булевой функции. Привести пример монотонной и
немонотонной булевой функции.
Функцию
f
∊
Р2,n
называют монотонной, если для любых
наборов
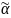 ,
,
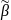 ∊
∊
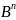 ,
таких, что
<=
,
имеет место f(
)
< f(
).
,
таких, что
<=
,
имеет место f(
)
< f(
).
Штрих Шеффера немонотонная
Дать определение полинома Жегалкина. Описать способ построения полинома Же
галкина с помощью метода неопределённых коэффициентов.
Дать определение двойственной булевой функции. Привести примеры двойствен-
ных функций.
Дать определение самодвойственной булевой функции. Привести пример само-
двойственной и несамодвойственной функции.
Дать определение замкнутого множества булевых функций. Привести пример.
Дать определение полной системы булевых функций. Привести пример полной си-
стемы.Перечислить классы Поста.
32. Сформулировать критерий Поста полноты системы булевых функций.
33. Записать стандартный базис, базис Жегалкина. Привести пример полной системы,
состоящей из одной булевой функции.
34. Дать определение нелинейной булевой функции. Привести пример полинома Жегалкина для функции существенно зависящей от трёх переменных__
