Закон распределения непрерывной случайной величины. Плотность распределения вероятности.

Для непрерывных случайных величин невозможно применить закон распределения в формах, приведенных выше, т.к. непрерывная величина имеет бесчисленное («несчетное») множество возможных значений, сплошь заполняющих некоторый интервал. Поэтому составить таблицу, в которой были бы перечислены все ее возможные значения, или построить многоугольник распределения нельзя.

Рассмотрим непрерывную случайную величину Х, возможные значения которой сплошь заполняют некоторый интервал (а, b)^. Закон распределения вероятностей такой величины может быть задан в виде функции распределения.

Функцией распределения случайной величины X называется вероятность события, состоящего в том, что случайная величина X примет значение меньшее x:

Функция – производная функции распределения (1) – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины X.

Формула (1) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразим функцию распределения через плотность.

.           

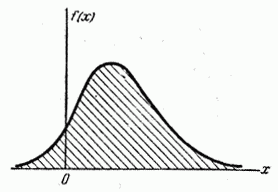
Кривая при этом называется кривой распределения.

Именно задание функции полностью определяет закон распределения для непрерывных случайных величин Х.

Для плотности распределения вероятности должно выполняться условие нормировки в виде:

(2)

если известно, что все значения Х лежат в интервале (а, b), или в виде:

(3)

если границы интервала для значений Х точно неизвестны. Условия нормировки плотности вероятности (2) или (3) являются следствием того, что значения случайной величины Х достоверно лежат в пределах (а, b) или (-, +).

Вероятность того, что случайная величина X примет значение из отрезка вычисляется по формуле

или

Пример 2. Непрерывная случайная величина Х задана плотностью вероятностей:

Найдите: а) постоянный параметр ; б) функцию распределения ; в) вероятность того, что в результате испытания Х примет значение из интервала .

Решение. а) По свойству дифференциальной функции .

В частности, если все возможные значения случайной величины Х принадлежат интервалу ,

то .

Найдём . Следовательно, .

Т.о., плотность вероятностей имеет вид .

б) Для нахождения функции распределения воспользуемся формулой .

Если , получаем .

Если , находим .

Если , то

Т.о., искомая интегральная функция распределения имеет вид:

в) Вероятность того, что в результате испытания Х примет значение из интервала , равна .

Задачи для самостоятельной работы

1. Стрелок производит три выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывается 5 очков. Построить ряд распределения числа выбитых очков.

2. Производится три независимых выстрела по мишени; вероятность попадания при каждом выстреле равна 0,7. Построить ряд распределения случайной величины X – числа попаданий.

3. В коробке 7 карандашей, из которых 4 красные. Из этой коробки наугад вынимают 3 карандаша. Найти закон распределения дискретной случайной величины Х, равной числу красных карандашей в выборке.

4. В партии из 8 деталей имеется 4 бракованных. Из партии наугад выбирают 3 детали. Составьте закон распределения дискретной случайной величины Х – числа бракованных деталей среди отобранных.

5. Дискретная случайная величина X имеет закон распределения:

	0	0,2	0,4	0,6	0,8
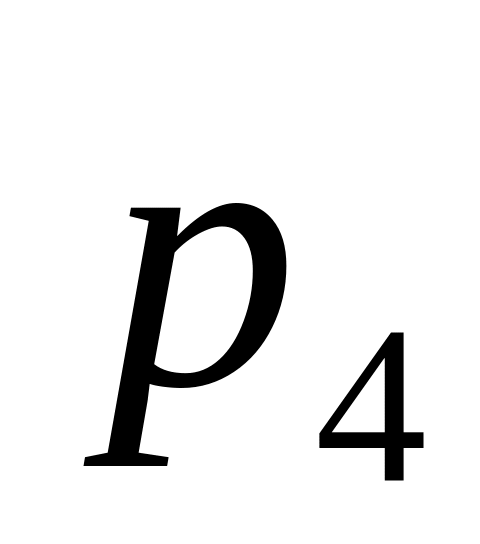
	0,15	0,2	0,3		0,15

Чему равна вероятность ? Постройте многоугольник распределения.

6. Дискретная случайная величина X имеет закон распределения:

	1	2	3	4	5
		0,15	0,30	0,25

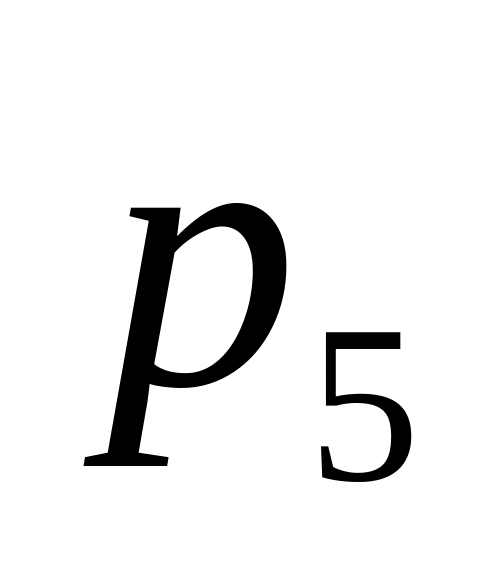
Найдите вероятность и , если известно, что в 2 раза больше .

7. Закон распределения дискретной случайной величины задан следующей таблицей:

	0	1	2	3
	0,2	0,4	0,3	0,1

Найдите функцию распределения этой случайной величины и постройте ее график.

8. Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка при одном выстреле , для второго – 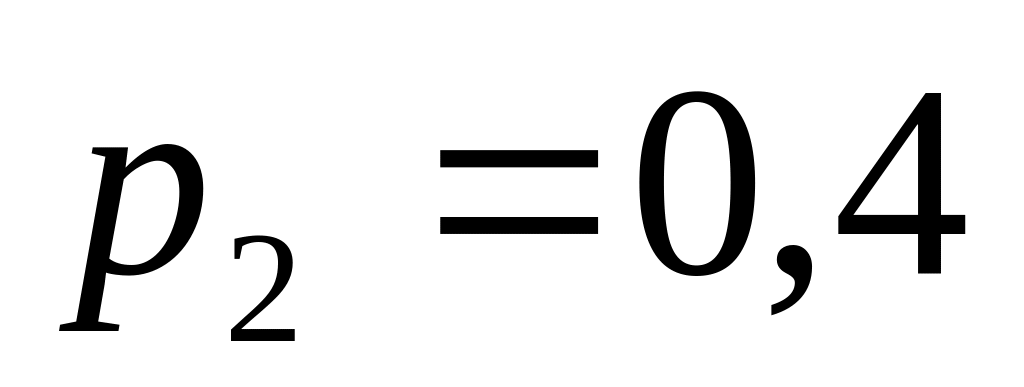. Дискретная случайная величина Х – число попаданий в мишень. Найти функцию распределения этой случайной величины. Найти вероятность события .

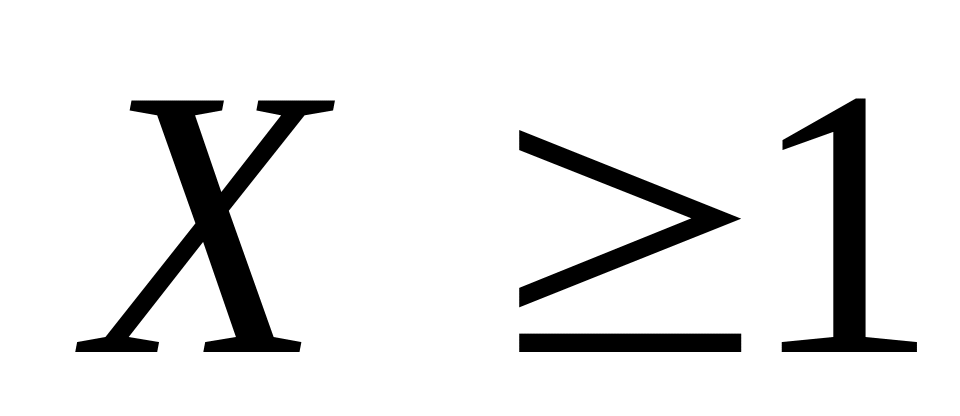9. Случайная величина Х задана интегральной функцией .

Найти а) дифференциальную функцию распределения; б) вероятность того, что случайная величина Х примет значение в интервале .

10. Плотность вероятности случайной величины Х задана функцией

.

Найти вероятность того, что в результате испытания величина Х примет значение из интервала .

11. Найти функцию распределения случайной величины Х, плотность вероятности которой определена функцией

12. Случайная величина Х задана интегральной функцией .

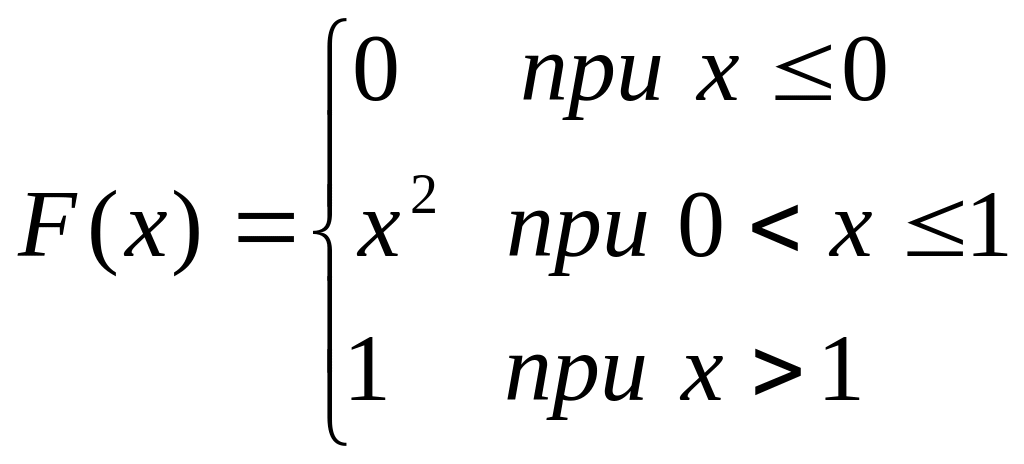Найти: а) дифференциальную функцию распределения; б) вероятность того, что случайная величина Х примет значение в интервале .

13. Непрерывная случайная величина Х задана плотностью вероятностей:

Найдите: а) постоянный параметр ; б) функцию распределения ; в) вероятность того, что в результате испытания Х примет значение из интервала

14. Непрерывная случайная величина Х задана плотностью вероятностей:

Найдите: а) постоянный параметр ;б) функцию распределения ; в) вероятность того, что в результате испытания Х примет значение из интервала .