Глава 9. Обобщение методов вычисления размерных коэффициентов аналитических моделей объектов и систем на многофакторный эксперимент.

Допустим, что проведенный эксперимент имеет r факторов и что функция отклика и факторы связаны линейно:

y_i = b₀ + b₁x _i1 + ... + b_r x_ir + ε_i, . (9.1)

В случае многих переменных более удобной оказывается матричная форма записи всех необходимых в данной задаче соотношений. Введем следующие матрицы:

;

; .

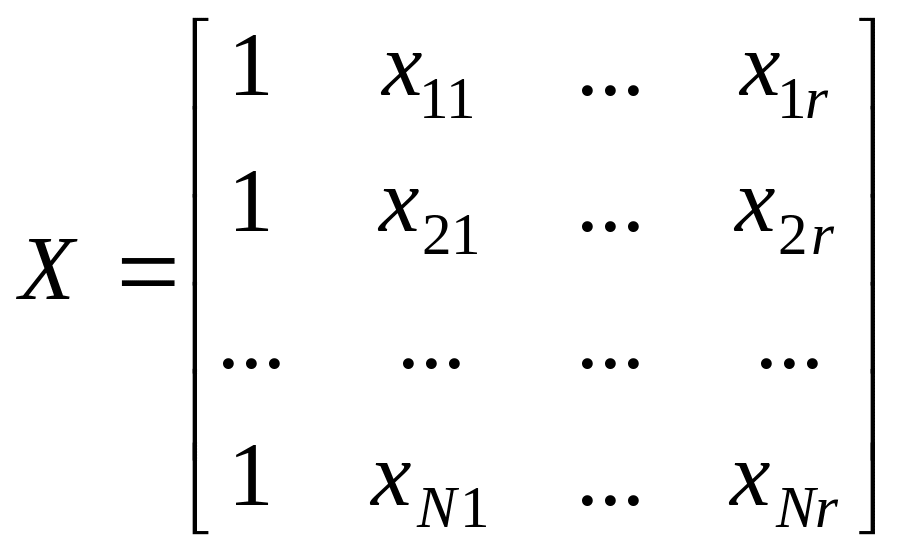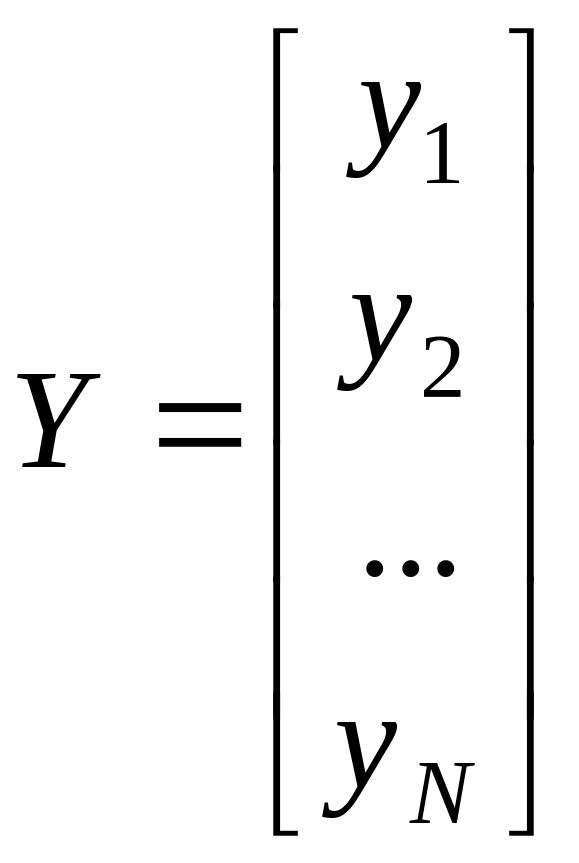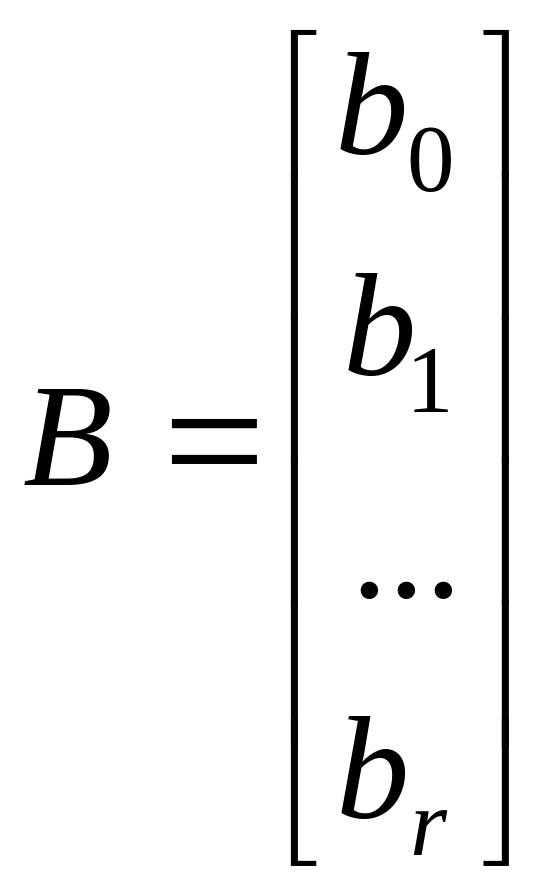Здесь Х – матрица факторов (условий опыта); Y– вектор столбец значений функции отклика; B – вектор столбец коэффициентов. Тогда систему (9.1) можно записать в матричном виде: Х В = Y.

Система нормальных уравнений МНК для определения коэффициентов для модели вида (9.1) имеет вид:

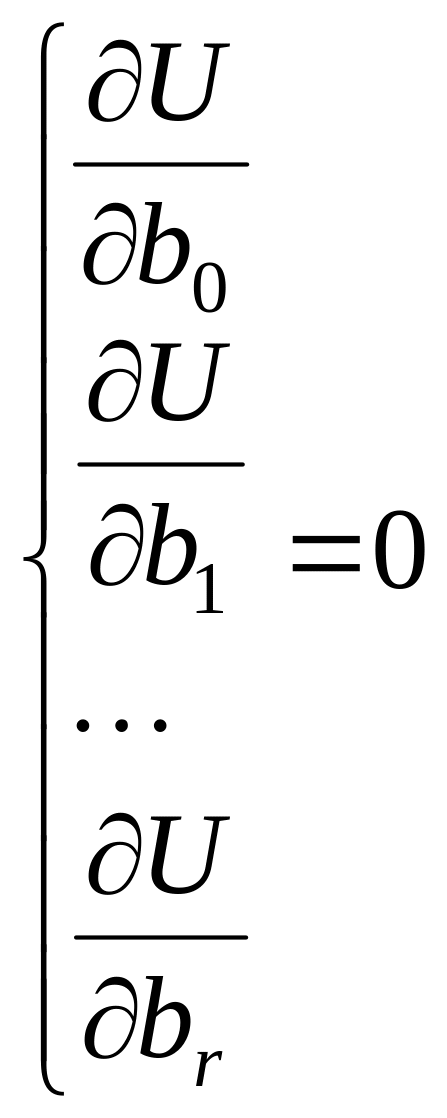, (9.2)

где или в матричной форме

U = (Y – XB)^T(Y – XB). (9.3)

Минимум функции, если он существует, достигается при одновременном равенстве нулю частных производных по всем переменным.

Дифференцируя выражение (9.3) по переменным b_i (i = 1, 2, …, r) в соответствии с правилами матричного дифференцирования линейных и квадратичных функций получим

, (9.4)

где 0 – вектор-столбец размерности r+1, состоящий из нулей,

.

Разрешая систему уравнений (9.4) относительно B получим систему уравнений в нормальном виде:

= , (9.5)

где X^T – матрица условий опыта (факторов ) транспонирования по отношению к матрице Х. Матрица называется матрицей системы нормальных уравнений МНК.

Решим эту систему. Помножим правую и левую часть (9.5) на матрицу, обратную к матрице системы нормальных уравнений МНК:

В = (9.6)

Произведение прямой матрицы на обратную равно единичной матрице:

Е = (9.7)

Умножение вектора В на единичную матрицу Е его не изменяет и поэтому имеем выражение для определения коэффициентов в виде:

В = . (9.8)

Замечание. Поскольку вырожденная, сингулярная матрица (определитель, которой равен нулю) не имеет обратной, то решение системы нормальных уравнений возможно, если матрица системы невырождена, т.е. det 0.

Матрица системы нормальных уравнений МНК часто бывает вырожденной вследствие того, что факторы линейно связаны с другими независимыми переменными.

Необходимо отметить, что на практике бывают ситуации, когда линейные модели оказываются неадекватными, а переход к полиномам более высокого порядка невозможен ввиду плохой обусловленности матрицы нормальных уравнений, т.е. близости к нулю ее определителя. Это является нарушением четвертой предпосылки регрессионного анализа для нелинейных членов уравнения регрессии.

Для реализации метода множественной линейной регрессии в MATLAB используется функция B=regress(Y,X), вычисляющая вектор коэффициентов B в соответствии с формулой (9.8).

Глава 10. Проверка адекватности модели.

Уравнение регрессии, полученное после вычисления коэффициентов, подвергают статистической обработке. При этом осуществляют проверку:

• адекватности математической модели;

• значимости коэффициентов регрессии.

Чтобы проверить адекватность модели по опытным данным, достаточно оценить отклонение предсказанных по уравнению регрессии значений отклика от результатов наблюдения y в одних и тех же i-х точках факторного пространства. Разность между опытным значением отклика и значением, найденным по уравнению регрессии, принято называть остатком, сумму квадратов остатков – остаточной суммой квадратов.

Рассеяние результатов наблюдения вблизи линии уравнения регрессии, оценивающего истинную функцию отклика, можно охарактеризовать с помощью остаточной дисперсии:

(10.1)

где d – число коэффициентов регрессии. Остаточная дисперсия определяется числом степеней свободы

_R = N – d. (10.2)

Если остаточная дисперсия незначимо отличается от дисперсии воспроизводимости эксперимента , то уравнение регрессии адекватно описывает опытные данные. Адекватность уравнения регрессии указывает на то, что его точность соответствует точности эксперимента и, следовательно, уравнение, обладающее более высокой точностью получить нельзя.

Если остаточная дисперсия значительно ниже дисперсии воспроизводимости, то это указывает на включение в уравнение регрессии членов, не несущих информации о влиянии факторов на отклик системы, или на неправильное применение формул регрессионного анализа.

В отдельных случаях, когда параллельные опыты ставятся только в части экспериментальных точек, найденная по этим данным дисперсия не характеризует воспроизводимости во всей области изменения факторов. Тогда ситуация < может служить косвенным указанием на отсутствие однородности дисперсий воспроизводимости в точках.

Проверка адекватности осуществляют с помощью критерия Фишера. Если > , то вычисляют дисперсионное отношение

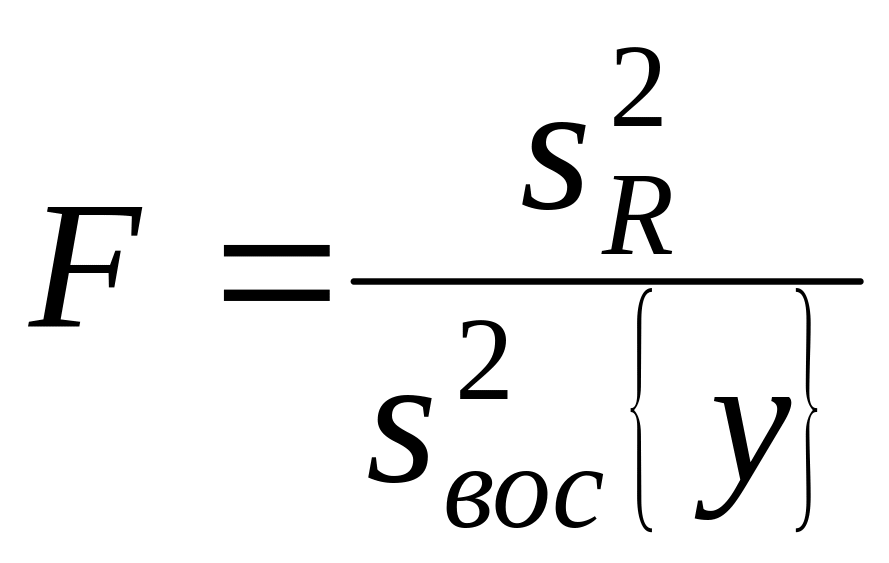. (10.3)

Если вычисленное значение меньше табличного значения F_кр критерия Фишера, найденного для соответствующих степеней свободы

₁ = N – d, ₂ = N (m–1) (10.4)

при заданном уровне значимости (обычно задают равным 5%), то гипотезу об адекватности не отвергают. В противном случае гипотезу отвергают, и математическое описание признается неадекватным.

Универсальным измерителем степени статистической связи между y и факторами x₁, x₂, …, x_n, является коэффициент детерминации К_д, который определяется соотношением

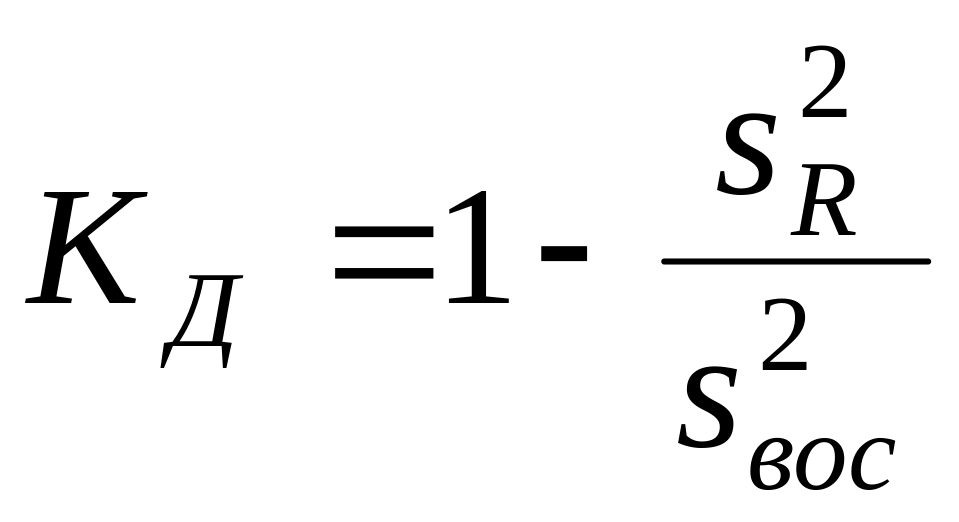, (10.5)

где – остаточная дисперсии; – дисперсия воспроизводимости эксперимента.

Коэффициент детерминации лежит в интервале [0,1]. Нулевое значение коэффициента детерминации соответствует полному отсутствию какой-либо связи между y и факторами x₁, x₁, …, x_r. Значение коэффициента равное 1 соответствует случаю чисто функциональной зависимости между y и факторами, когда значение y может быть в точности (детерминированно) восстановлено по значениям x₁, x₁, …, x_n, с помощью формулы y=f(x₁, x₁, …, x_r).

Численное значение коэффициента детерминации К_д отражает долю общей вариации функции отклика y, объясненную функцией регрессии. Например, если коэффициент детерминации равен 0,769, то это означает, что 76,9% изменения величины отклика может быть объяснено регрессией. Таким образом, чем больше К_д, тем лучше модель аппроксимирует Y.

В моделях линейной регрессии в качестве измерителя степени статистической связи между y и факторами x₁, x₂, …, x_n, используется множественный коэффициент корреляции R. Он определяется как обычный парный коэффициент корреляции между y и линейной функции регрессии по x₁, x₁, …, x_r, т.е.

f(x₁, x₁, …, x_n) = b₀ + b₁x₁ + ... + b_r x_r

В этом случае коэффициент детерминации равен квадрату множественного коэффициента корреляции, т.е. К_д = R².

Проверка значимости коэффициентов регрессии. Оценки дисперсий коэффициентов регрессии b_i вычисляются по формуле

,

где – остаточная дисперсия, c_ii – i-й диагональный элемент матрицы .

Проверку значимости коэффициентов регрессии производят с помощью критерия Стьюдента, эмпирическое значение которого

. (10.6)

Если найденное значение параметра t_э превышает значение t для числа степеней свободы  = n (m–1) при заданном уровне значимости p (обычно 5 ) (Приложение 1), то коэффициент признают значимым. В противном случае коэффициент принимается равным нулю с вероятностью ошибки p.

Факторы, имеющие большие значения t_э оказывают более существенное влияние на отклик системы. Если коэффициент не значим, то соответствующий фактор можно исключить из уравнения регрессии. Эту процедуру необходимо проводить с большой осторожностью. При наличии значительной корреляции между коэффициентами регрессии возможны существенные изменения в величинах остальных коэффициентов. Поэтому исключение членов из уравнения должно сопровождаться повторным вычислением коэффициентов регрессии и повторной проверкой адекватности уравнения регрессии.

Можно построить доверительный интервал

b_j =  t s{b_j}, (10.7)

здесь t – табличное значение коэффициента Стьюдента; s{b_j} – среднеквадратичная ошибка коэффициента регрессии.

По умолчанию доверительные интервалы строятся с 95% вероятностью .

Анализ остатков. Остаточная дисперсия является усредненной оценкой точности математической модели. Поэтому дисперсионное отношение также есть усредненная оценка качества уравнения регрессии. Исследователя часто интересует не только усредненная характеристика, но и отклонения (остатки) в отдельных точках, анализ которых может дать дополнительную информацию о процессе. Анализ остатков проводят визуально посредством нанесения их на график. Если модель адекватно описывает экспериментальные данные и не содержит никаких нарушений, то остатки случайно распределены в пределах доверительного интервала, представляющего собой горизонтальную полосу с центром на оси абсцисс.

Наиболее часто встречаются следующие нарушения распределения остатков.

1. Если остатки находятся внутри расширяющейся полосы, это указывает на отсутствие постоянства дисперсии; если полоса не горизонтальна, это дает основание для введения в модель дополнительной независимой переменной.

2. Наличие выбросов, т.е. отдельных остатков, превосходящих доверительный интервал по абсолютной величине. Существование выбросов может быть связано с нарушением режима проведения эксперимента в данной точке. В этом случае необходима постановка дополнительных экспериментов в точках выбросов. Если эта причина не подтверждается, то наличие выбросов может быть связано с несоответствием вида математической модели действительной форме поверхности отклика.