Порядок

проведения обработки результатов наблюдений.

Обработка ре зультатов многократных измерений должна проводиться в соответствии с ГОСТ 8.207.76 “ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения”

Исходной информацией для обработки является ряд из n (n > 4) результатов измерений y₁, y₂, y₃, …, y_n, из которых исключены известные систематические погрешности, – выборка.

Последовательность обработки результатов прямых многократных измерений состоит из ряда этапов.

1. Определение точечных оценок закона распределения результатов измерений.

На этом этапе определяются:

• среднее арифметическое значение измеряемой величины по формуле (7.1);

• среднеквадратическое отклонение результата измерения S_y по формуле (7.3);

В соответствии с рассмотренными выше критериями исключаются грубые погрешности, после чего проводится повторный расчет оценок среднее арифметического значения и его среднеквадратического отклонения.

2. Определение закона распределения результатов измерений или случайных погрешностей измерений. При числе наблюдений n>50 для идентификации закона распределения используется критерий Пирсона. При 50 > n > 15 для проверки нормальности закона распределения применяется составной критерий (d-критерий), приведенный в ГОСТ 8.207-76. При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.

3. Определение доверительных границ случайной погрешности. Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находят квантильный множитель z_p при заданном значении доверительной вероятности P. В этом случае доверительные границы случайной погрешности Δ = .

4. Определение границ неисключенной систематической погрешности θ результата измерений [5].

5. Определение доверительных границ погрешности результата измерений Δ_р. Данная операция осуществляется путем суммирования среднеквадратического отклонения случайной составляющей и границ неисключенной систематической погрешности θ в зависимости от соотношения по правилам суммирования погрешностей [5].

6. Запись результата измерения. Результат измерения записывают в виде при доверительной вероятности P = P_д.

Глава 8. Вычисление размерных коэффициентов аналитических моделей объектов и систем по результатам однофакторного эксперимента.

Как уже отмечалось, задачей эксперимента является получение данных необходимых для установления математической модели (аналитической зависимости), описывающей характеристику устройства или системы, которая в общем виде записывается

y = f (x₁,x₂,...,x_r) + ε, (8.1)

где y – выходная характеристика устройства или системы; x₁, x₂,..., x_r – входные сигналы и внешние факторы, определяющие поведение устройства или системы, ε – случайная “остаточная” составляющая. Наличие случайной составляющей ε в уравнении (8.1) обусловлено причинами двоякой природы: во-первых, она отражает влияние на формирование значений y факторов, не учтенных в перечне переменных x_i; во-вторых, она может включать в себя случайную погрешность в измерении выходной характеристики y.

Установление математической модели включает в себя выбор вида математической модели и определение ее параметров (коэффициентов, показателей степени и т.п.). Объективный анализ связи между величинами в значительной степени должен основываться на статистических методах.

Для решения задачи построения математической модели системы используется статистический метод обработки наблюдений – метод регрессионного анализа.

В схеме регрессионного анализа предполагается, что независимые переменные (факторы) x_i являются неслучайными величинами, значения которых задаются заранее, перед началом эксперимента; зависимая переменная y – случайная величина.

Нас интересует только среднее значение y при заданных x_i – , т.е. функциональная зависимость условного среднего значения функции отклика y (при условии, что факторы x_i , , фиксированы) от x_i:

= f(x₁, x₂,..., x_r, b₀, b₁, b₂, …).

Предполагается, что математическое ожидание, от случайной составляющей ε в уравнении (8.1) равно нулю: M[ε] = 0.

В регрессионном анализе вид функции предполагается известным и по результатам эксперимента нужно значения неизвестных коэффициентов модели b₀, b₁, b₂,… При выборе вида кривой регрессии следует использовать экспертные оценки, т.е. совокупность сведений профессионального характера об изучаемом реальном устройстве или системе.

Обоснованное применение регрессионного анализа требует выполнения ряда предпосылок:

1) при каждых значениях x_i, , величина y распределена нормально;

2) дисперсия D[y(x)] величины y постоянна:D[y(x)] = σ², где σ = const.

3) наблюдения являются стохастически независимыми.

4) факторы не должны быть линейно связаны с другими независимыми переменными.

Замечание. Третье условие регрессионного анализа часто нарушается при использовании времени в качестве одного из факторов.

Существует много разнообразных методов обработки результатов эксперимента. Обоснованный и точный выбор метода для оценки параметров математической модели опирается на знание вероятностной природы (типа закона распределения) остатков ε в модели (8.1). Если при любых значениях x_i, , распределение вероятностей остатков ε описывается нормальным законом, и остатки ε(x_i) статистически независимы, то наилучшие оценки для параметров получаются при применении метода наименьших квадратов.

Рассмотрим применение метода наименьших квадратов для определения коэффициентов b₀ и b₁ линейной функции отклика с одним фактором вида

y = b₀ + b₁ x . (8.2)

Если бы все экспериментальные точки лежали строго на прямой линии, то для каждой из них было бы справедливо равенство

y_i – b₀ – b₁ x_i = 0, (8.3)

где i = 1, 2, ... , n – номер опыта. На практике это неравенство нарушается и вместо него используется:

y_i – b₀ – b₁ x_i = _i , (8.4)

где _i – разность между экспериментальным и вычисленным по уравнению регрессии значениями y в i-ой экспериментальной точке, эту величину называют невязкой.

Необходимо найти такие коэффициенты регрессии, при которых невязки будут минимальны. Выражение минимизации невязки

(8.5)

приводит к методу наименьших квадратов (МНК). Уравнение регрессии содержит два неизвестных коэффициента. Значит, применяя МНК, получим два уравнения. Соотношение (8.5) запишем в следующем виде:

(8.6)

Минимум функции достигается при одновременном равенстве нулю частных производных по всем неизвестным:

(8.7)

Из соотношения (8.6) с учетом (8.7) получаем уравнения для определения коэффициентов функции отклика

(8.8)

если раскрыть скобки, то получим

(8.9)

Окончательно формулы для вычисления коэффициентов регрессии имеют вид

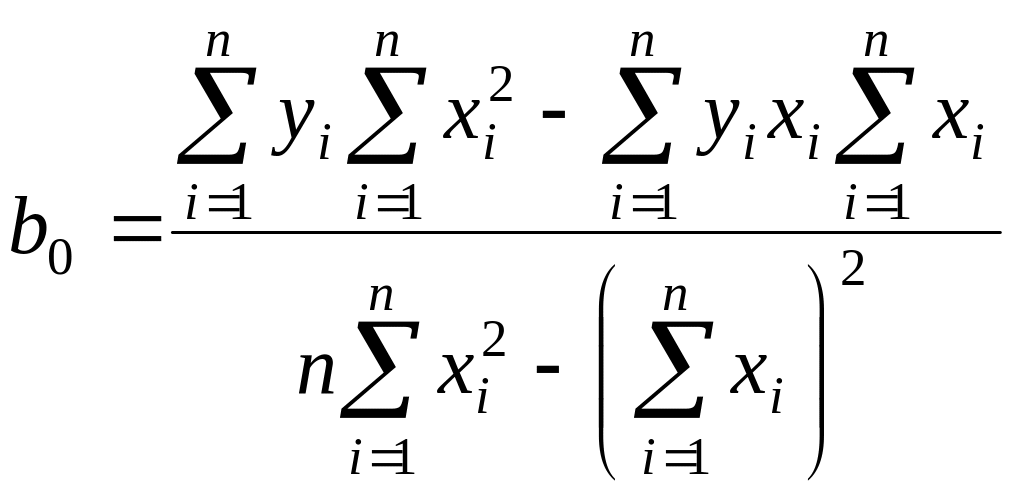, (8.10)

.

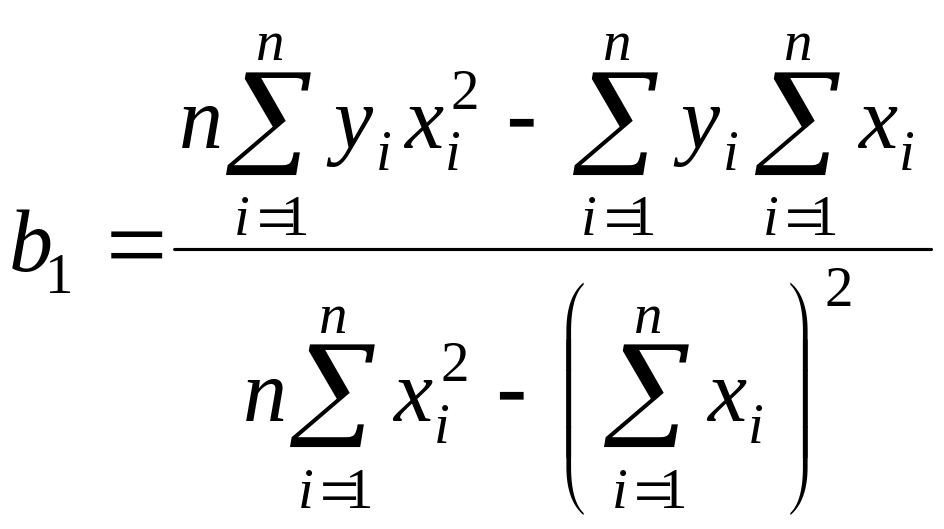График аппроксимирующего линейного полинома представлен на рис.2. Экспериментально полученные результатам обозначены кружками.

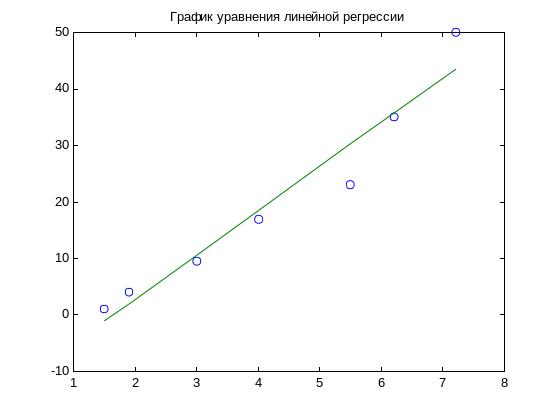
Рис. 2.