ВВЕДЕНИЕ

Настоящие методические указания предназначены для студентов всех специальностей и направлений бакалаврской подготовки заочной формы обучения, выполняющих расчетно-графическую работу по линейной алгебре, аналитической геометрии и введению в анализ. Приведенные краткие теоретические сведения, типовые задачи и примеры по каждому разделу позволяют успешно справиться с аналогическими заданиями самостоятельно и способствуют формированию предметного представления о соотношении теоретических и практических результатов.

1. Вычисление определителей

1.1. Определители второго порядка

Определителем второго порядка называется число:

.

Определение показывает несложность вычисления определителей второго порядка.

Примеры.

1.2. Определители третьего порядка

Определителем третьего порядка называется число, которое может быть вычислено по следующему правилу (правило Саррюса): к определителю справа приписывается первый и второй столбцы и элементы, стоящие на диагоналях полученной таблицы, перемножаются, а затем эти произведения складываются, причем произведения элементов на диагоналях, идущих снизу вверх, берутся со знаком минус:

_.

Примеры.

а) -

-15-24-24=0

б)

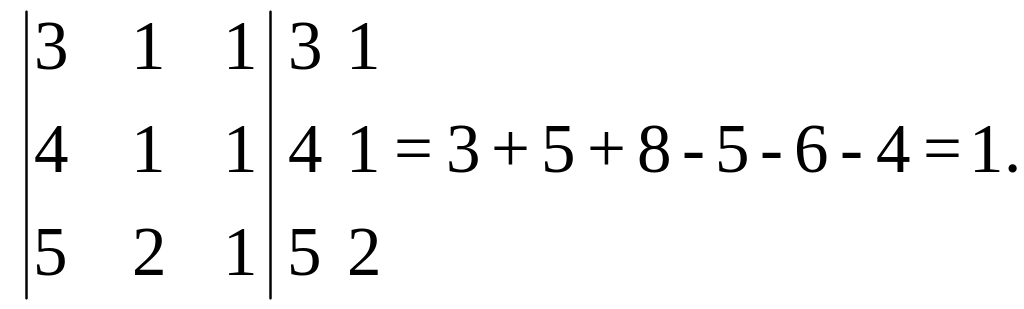
3. Задачи для самостоятельного решения

Вычислить определители второго и третьего порядка:

а) б) ; в)

1.4. Определители произвольного порядка

Пусть задан определитель n-го порядка

.

Для любого определителя выполнены свойства:

а) если в определителе две строки или два столбца равны, то определитель равен нулю:

б) если в определителе какая-либо строка или столбец состоит из нулей, то этот определитель равен нулю:

в) общий множитель в строке или столбце можно вынести за знак определителя:

г) если в определителе поменять местами две строки или два столбца, то определитель изменит знак:

д) определитель не изменится, если к произвольной строке прибавить другую строку, домноженную на любое число. Это же справедливо и для столбцов. Например, в следующем определителе к третьей строке добавлена первая, домноженная на минус два:

Для вычисления определителей специального треугольного вида применимо следующее правило:

_.

Свойства определителей позволяют любой определитель свести к треугольному виду и вычислить его по указанному правилу.

Примеры.

а) (ко второй строке прибавляем первую, домноженную на (-2), к третьей строке прибавляем первую, домноженную на (-3), к четвертой строке прибавляем первую, домноженную на (-8))

(к третьей строке прибавляем вторую, домноженную на (-2))

(по второму свойству определителей).

б) (поменяем вторую и первую строки местами, чтобы иметь единицу на первом месте в первой строке) =

(ко второй строке прибавляем первую, домноженную на (-3) и т.д.) =

.

в) (к третьей строке прибавляем вторую, домноженную на (-1), к четвертой строке прибавляем третью, домноженную на (-1), для уменьшения чисел в первом столбце)

1.5. Задачи для самостоятельного решения

Вычислить определители:

2. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ

2.1. Понятие матрицы

Матрицей порядка nm называется прямоугольная таблица чисел вида

.

Числа а_ij называются элементами матрицы. Матрицу будем коротко записывать = (а_ij) _nm . Если n=m, то матрица называется квадратной порядка n.

Матрица с элементами (i,j=1,2,…,n) называется единичной матрицей n-го порядка.

2.2. Умножение матрицы на число

Чтобы умножить матрицу А на число , необходимо умножить каждый элемент матрицы на это число.

Пример. Для матрицы найдем произведение . Из определения получаем

2.3. Сложение матриц

Если матрица В = (b_ij)_nm имеет тот же порядок, что и матрица А = =(а_ij)_nm, то можно определить их сумму - матрицу С = А + В = (c_ij)_nm того же порядка - по правилу: с_{ij =} а_ij + b_ij для i =1, 2,..., n; j = 1, 2,..., m. Матрицы различных порядков складывать нельзя.

Пример. Найдем сумму матриц А + В, где

2.4. Умножение матриц

Произведением матрицы А = (а_ij)_nm на матрицу В = (b_ij)_mp называется матрица С = А В = (с_ij)_np, построенная по правилу

Практически перемножение матриц осуществляется следующим образом: берут i-ю строку матрицы А, умножают ее поэлементно на j-й столбец матрицы В и эти произведения складывают. Полученное число является элементом матрицы С, стоящим в i-й строке и j-м столбце.

Пример. Найдем произведение матриц АВ, если

Внимание:

а) матрица А имеет порядок nm, матрица В имеет порядок mp, а их произведение АВ - порядок np;

б) в общем случае АВ  ВА.

Примеры.

а) Найдем ВА, где матрицы А и В взяты из предыдущего примера:

б) Найдем значение матричного многочлена В = 2А² + 3А + 5Е, где

- единичная матрица третьего порядка.

Имеем

тогда