9562

Из формул следует, что выражения моментов, углов поворота и прогибов преды-

дущих участков входят как составная часть выражений для последнего (4-го ) участка балки. Это позволяет результаты решения для всех участков объединить и записать формулы для углов поворота и прогибов в виде единого выражения для всех участков,

используя следующий приём:

Применяя правило, из формулы для погибов 4-го участка при z < a получим выражение прогиба 1-го участка, при z < b получим выражение прогиба 2-го участка,

при z < c получим выражение прогиба 3-го участка.

Таким образом, для уравнения прогибов балки с учётом можно записать обобщённое уравнение прогибов в виде:

Уравнение является универсальным уравнением прогибов балки, поскольку может быть использовано для определения прогибов для балки с любым числом участков.

Определение прогибов балок с помощью универсального уравнения требует вы-

полнения следующих правил.

1.Уравнение применимо для решения балок только с постоянной жёсткостью EJx = const.

2.Начало координат необходимо помещать либо на левом конце балки, либо на пра-

вом конце балки.

3.Знак «плюс» перед квадратными скобками следует выбирать, если ось у направить вверх, а знак «минус», если ось у направить вниз.

4.Прогиб балки всегда выражается через четыре начальных параметра: два статиче-

ских Мо, Qo и два геометрических vo, θo, поэтому метод называется методом на-

чальных параметров.

5.Неизвестный прогиб vo и угол поворота θo в начале координат необходимо опреде-

лять из условий закрепления балки .В частности:

∙ если в начале координат расположена жёсткая заделка, то vo = 0 и θo = 0;

6.При использовании универсального уравнения условия плавности и непрерывности на границах участков балки выполняются автоматически.

7.Знак слагаемых, стоящих в квадратных скобках, определяют по правилу знаков для изгибающих моментов. В частности:

∙если силы F и нагрузки q направлены вверх, то изгибающие моменты от такой нагрузки будут положительными независимо от выбора положения начала коор-

динат;

∙если силы F и нагрузки q направлены вниз, то изгибающие моменты от такой нагрузки будут всегда отрицательными;

∙изгибающие моменты от моментной нагрузки будут положительными, если со-

средоточенные моменты М действуют по часовой стрелке при размещении на-

чала координат на левом конце балки;

∙при размещении начала координат на правом конце балки сосредоточенный мо-

мент М необходимо вводить в уравнение со знаком «плюс», если он действует против часовой стрелки.

8.Универсальное уравнение углов поворота сечений балки получается из уравнения путём его дифференцирования: EJxθ(z) = EJxv′ (z).

Лекция №9

Напряженно-деформированное состояние в точке.

Обобщенный закон Гука

Значения нормальных и касательных напряжений на произвольных площадках,

проходящих через какую-либо точку тела, зависят от положения этих площадок.

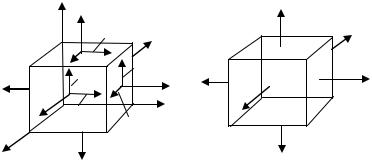
На рис. 57 показаны три взаимно перпендикулярные произвольные площадки, на гранях которых действуют нормальные и касательные напряжения. Нормальные на-

пряжения показаны растягивающими, т.е. положительными. Касательные напряжения

(на каждой грани по два) показаны с двумя индексами: первый индекс указывает па-

раллельно какой оси координат действует, а второй – на грани с какой нормалью. В

общем случае напряженное состояние в точке описывается тензором напряжений

На рис. 58 показан параллелепипед с бесконечно малыми размерами сторон,

грани которого являются главными площадками, так как на них отсутствуют касатель-

ные напряжения. В зависимости от наличия отличных от нуля главных напряжений на главных площадках различают три вида напряженных состояний:

Рис.58

1.Если все три главных напряжения отличны от нуля, то имеет место в данной точке объемное или пространственное напряженное состояние (ОНС).

2.В том случае, когда два главных напряжения отличны от нуля, а одно равно ну-

лю – имеет место плоское напряженное состояние (ПНС).

3.Если только одно главное напряжение отлично от нуля, а два других равны ну-

лю, имеет место одноосное (линейное) напряженное состояние (ЛНС).

Наиболее простым и наглядным случаем одноосного (линейного) напряженного со-

стояния является центральное растяжение– сжатие стержней. Определение напряжений на наклонных площадках при ЛНС было исследовано в предыдущей лекции.

Установим зависимость относительной линейной деформации от нормальных на-

пряжений в случае объемного напряженного состояния.

Определим относительную продольную деформацию выделенного элемента в на-

правлении главного напряжения σ1, отдельно рассматривая влияние каждого из глав-

ных напряжений и складывая результаты в соответствии с принципом независимости действия сил:

ε1 = ε11 + ε12 + ε13 .

Под действием напряжения σ1 элемент в направлении этого напряжения на основа-

нии закона Гука получит относительное удлинение, равное ε11 = σ1 . (Аналогично оп-

Е

ределятся относительные деформации по направлениям двух других главных напряже-

няются относительные линейные деформации и углы сдвига граней выделенного эле-

мента с бесконечно малыми размерами dx, dy, dz.

Совокупность линейных относительных деформаций и углов сдвига для всевоз-

можных направлений осей, проведенных через заданную точку, называется деформи-

рованным состоянием в точке.

Деформации элемента в трех ортогональных плоскостях представим в виде таблицы

аналогичной тензору напряжений и называемой тензором деформаций.

Выражения, устанавливающие связь между деформациями и напряжениями в об-

щем случае напряженного состояния, носят название обобщенного закона Гука. Они применимы при напряжениях, не превышающих предел пропорциональности материа-

ла и при малых деформациях.

С помощью формул обобщенного закона Гука можно определять относительные деформации по любому заданному направлению, если предварительно определить нормальные напряжения вдоль указанного направления и двух других направлений,

перпендикулярных заданному.

Относительные деформации ε1, ε2, ε3 в направлениях, для которых отсутствуют углы сдвига, определяемые по формулам, называются главными деформациями.

Для главных направлений тензор деформаций получит вид:

Гипотезы прочности

В гипотезах прочности предлагаются критерии, определяющие прочность элемента материала, находящемся в сложном напряженном состоянии. Соответственно этим критериям установлены эквивалентные напряжения σэкв – напряжения одноосного рас-

тяжения элемента материала, который равнопрочен тому же элементу при сложном на-

пряженном состоянии. Вне зависимости от принятой гипотезы условие прочности элемен-

та материала при любом напряженном состоянии имеет вид:

σэкв ≤ [ σp ].

Для объемного напряженного состояния элемента эквивалентные напряжения имеют следующие значения :

по гипотезе наибольших нормальных напряжений

= σ1 при σ1 > 0,

по гипотезе наибольших линейных деформаций

σIIэкв = σ1 – µ(σ2 + σ3),

по гипотезе наибольших касательных напряжений

σIIIэкв = σ1 – σ3,

для плоского напряженного состояния:

для плоского напряженного состояния:

σVIэкв = σ 2 + 3τ 2 .

Лекция №10

ВНУТРЕННИЕ СИЛЫ ПРИ СЛОЖНОМ СОПРОТИВЛЕНИИ СТЕРЖНЯ

Правила построения эпюр при пространственном загружении стержня несколько отличаются от правил, принятых для построения эпюр усилий в стержне, на который действует нагрузка, расположенная в одной плоскости.

Перечислим эти отличия.

1.Эпюры Qx и Qy строятся на одной оси.

Эпюра строится в аксонометрии, причем ординаты Qx откладываются по оси х, ор-

динаты Qy ‒ по оси у.

Положительные значения поперечных сил откладываются в отрицательном направ-

лении соответствующих осей.

Такая результирующая эпюра поперечных сил обозначается просто Q.

2.Эпюры Mx и My строятся на одной оси.

Эпюра строится в аксонометрии, причем ординаты Mx откладываются перпендику-

лярно оси х (по оси у), а ординаты My по оси х.

Положительные значения изгибающих моментов откладываются в положительном направлении соответствующих осей (как в балках).

Полученная результирующая эпюра изгибающих моментов обозначается Mи. Зна-

ки на эпюре Mи не ставятся.

При построении эпюр изгибающего момента Mx в балках положительные значения

Mx откладываются вниз (в положительном направлении оси у и перпендикулярно оси х). В соответствии с правилом знаков при положительном изгибающем моменте в сече-

ниях балки растягиваются нижние волокна (волокном здесь называются совокупность точек, лежащих на линии, параллельной продольной оси z).

Таким образом, можно сказать, что положительные значения момента Mx на эпюре откладываются «от растянутого волокна». Более того, чтобы не связывать эпюру

Mи с выбором системы координат, знаки на эпюре не проставляются.

Если при построении пространственной эпюры поперечных сил Q возникают за-

труднения с определением знака, полезно использовать правило: при нисходящей эпю-

ре изгибающего момента поперечная сила положительна.

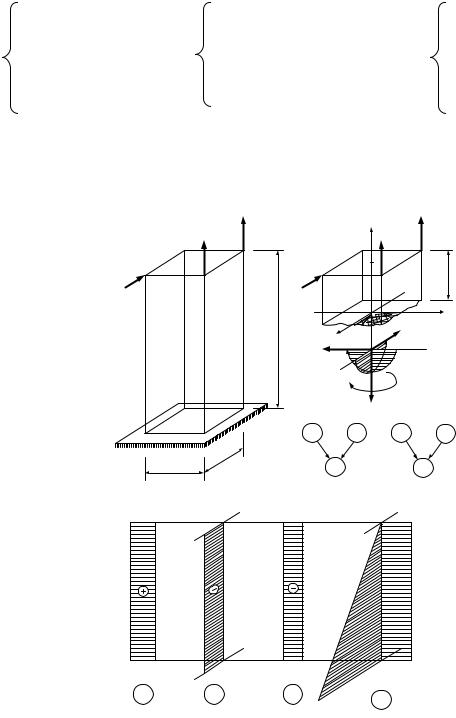
Пример 1. Построить эпюры внутренних сил для стержня, изображенного на рис. 59.

Решение

Воспользуемся методом сечений в чистом виде. Реакции в заделке в данном случае можно не определять, если рассматривать равновесие верхней части стержня.

Итак, проводим сечение на расстоянии z от верхнего края стержня. Нижнюю часть стержня отбрасываем. Действие нижней части стержня на верхнюю заменяем 6-ю

неизвестными компонентами внутренних сил. Поскольку их значения неизвестны, из-

начально будем считать их положительными. (Штриховкой показаны плоскости дейст-

вия моментов Мх и Му).

Для отсечной части стержня запишем шесть уравнений равновесия:

Задача. Построить эпюры внутренних сил для стержня, изображенного на рис.60.

Решение

Построить эпюры усилий в данном случае можно не определяя реакции в задел-

ке, которые в данном пространственном случае представлены шестью неизвестными компонентами.

Границы участков пронумерованы, и в каждом из этих сечений показана соот-

ветствующая система координат.

Так же, как и в балках, строить эпюры в данном случае можно «эскизным» спо-

собом, например, «по границам участков».

Для упрощения процесса построения эпюр рекомендуется:

1. Все внешние силы, действующие на стержень, привести к продольной оси z с

помощью теоремы о параллельном переносе силы, которая иллюстрируется рис. 61.

Так, при перенесении силы F1 по оси х добавляется момент M1 = F2·а, при перенесении силы F2 по оси y добавляется M2 = F2·2а, при перенесении силы F3 в точку С1 добавля-

ется в вертикальной плоскости момент М3 = F3·2а и в горизонтальной плоскости М4 = F3 · а .

2. Используя принцип независимости действия сил разбить всю нагрузку на три группы:

А) Нагрузку, проектирующуюся на оси z или вызывающую относительно ее мо-

мент. Это M1 , M2 и F3 .

Б) Нагрузку, вызывающую прямой поперечный изгиб в вертикальной плоскости.

Это F1 , М3 .

В) Нагрузку, вызывающую прямой поперечный изгиб в горизонтальной плоско-

сти. Это М4 и F2 .

Нагрузка группы А вызывает в сечениях стержня продольное усилие

N = - 4P и крутящий момент Мк = 2Ра на правом участке стержня. Каждая из этих эпюр строится на своей оси. Чтобы не привязывать эпюру к определенной координатной сис-

теме, соответствующая обозначена Мк .

Эпюры от нагрузки группы Б и В строятся как для обычной консольной балки :

от изгиба в вертикальной плоскости yz - эпюры Qy и Mx (ось x - вниз). Схема на рис. 62

помогает уяснить, как направление внешнего момента связано со знаком изгибающего момента. Проще говоря, где стрелка - там сжатая половина сечения.